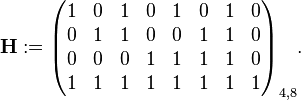海明码

来源：互联网发布：国家甲醛检测标准知乎编辑：程序博客网时间：2024/04/29 09:27

汉明码(Hamming Code)，是在电信领域的一种线性调试码，以发明者理查德·卫斯里·汉明的名字命名。汉明码在传输的信息流中插入验证码，以侦测并更正单一比特错误。由于汉明编码简单，它们被广泛应用于内存（RAM）。其 SECDED（single error correction, double error detection）版本另外加入一检测比特，可以侦测两个或以下同时发生的比特错误，并能够更正单一比特的错误。因此，当传送端与接收端的比特样式的汉明距离 (Hamming distance) 小于或等于1时（仅有 1 bit 发生错误），可实现可靠的通信。相对的，简单的奇偶检验码除了不能纠正错误之外，也只能侦测出奇数个的错误。

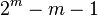在数学方面，汉明码是一种二元线性码。对于每一个整数 $m>2$ ，存在一个编码，带有 $m$ 个奇偶校验位 $2^m-m-1$ 个数据位。该奇偶检验矩阵的汉明码是通过列出所有米栏的长度是两两独立。

历史[编辑]

1940年，汉明于贝尔实验室(Bell Labs)工作，运用贝尔模型V(Bell Model V)计算机，一个周期时间在几秒钟内的机电继电器机器。输入端是依靠打孔卡(Punched Card)，这不免有些读取错误。在平日，特殊代码将发现错误并闪灯(flash lights)，使得操作者能够纠正这个错误。在周末和下班期间，在没有操作者的情况下，机器只会简单地转移到下一个工作。

汉明在周末工作，他对于不可靠的读卡机发生错误后，总是必须重新开始项目变得愈来愈沮丧。在接下来的几年中，他为了解决调试的问题，开发了功能日益强大的调试算法。在1950年，他发表了今日所称的汉明码。现在汉明码有着广泛的应用。

汉明码之前[编辑]

人们在汉明码出现之前使用过多种检查错误的编码方式，但是没有一个可以在和汉明码在相同空间消耗的情况下，得到相等的效果。

奇偶[编辑]

主条目：奇偶校验位

奇偶校验是一种添加一个奇偶位用来指示之前的数据中包含有奇数还是偶数个1的检验方式。如果在传输的过程中，有奇数个位发生了改变，那么这个错误将被检测出来（注意奇偶位本身也可能改变）。一般来说，如果数据中包含有奇数个1的话，则将奇偶位设定为1；反之，如果数据中有偶数个1的话，则将奇偶位设定为0。换句话说，原始数据和奇偶位组成的新数据中，将总共包含偶数个1.

奇偶校验并不总是有效，如果数据中有偶数个位发生变化，则奇偶位仍将是正确的，因此不能检测出错误。而且，即使奇偶校验检测出了错误，它也不能指出哪一位出现了错误，从而难以进行更正。数据必须整体丢弃并且重新传输。在一个噪音较大的媒介中，成功传输数据可能需要很长时间甚至不可能完成。虽然奇偶校验的效果不佳，但是由于他只需要一位额外的空间开销，因此这是开销最小的检测方式。并且，如果知道了发生错误的位，奇偶校验还可以恢复数据。

汉明码[编辑]

如果一条信息中包含更多用于纠错的位，且通过妥善安排这些纠错位使得不同的出错位产生不同的错误结果，那么我们就可以找出出错位了。在一个7位的信息中，单个位出错有7种可能，因此3个错误控制位就足以确定是否出错及哪一位出错了。

汉名研究了包括五取二码在内的编码方案，并归纳了他们的想法。

通用算法[编辑]

下列通用算法可以为任意位数字产生一个可以纠错一位（英语：Single Error Correcting）的汉明码。

从1开始给数字的数据位（从左向右）标上序号, 1，2，3，4，5...
将这些数据位的位置序号转换为二进制， 1, 10, 11, 100, 101, 等.
数据位的位置序号中所有为二的幂次方的位（编号1，2，4，8，等，即数据位位置序号的二进制表示中只有一个1）是校验位
所有其它位置的数据位（数据位位置序号的二进制表示中至少2个是1）是数据位
每一位的数据包含在特定的两个或两个以上的校验位中，这些校验位取决于这些数据位的位置数值的二进制表示
1. 校验位 1 覆盖了所有数据位位置序号的二进制表示倒数第一位是1的数据：1（校验位自身，这里都是二进制，下同），11，101，111，1001，等
2. 校验位 2 覆盖了所有数据位位置序号的二进制表示倒数第二位是1的数据：10（校验位自身），11，110，111，1010，1011，等
3. 校验位 4 覆盖了所有数据位位置序号的二进制表示倒数第三位是1的数据：100（校验位自身），101，110，111，1100，1101，1110，1111，等
4. 校验位 8 覆盖了所有数据位位置序号的二进制表示倒数第四位是1的数据：1000（校验位自身），1001，1010，1011，1100，1101，1110，1111，等
5. 简而言之，所有校验位覆盖了数据位置和该校验位位置的二进制与的值不为0的数。

采用奇校验还是偶校验都是可行的。偶校验从数学的角度看更简单一些，但在实践中并没有区别。

校验位一般的规律可以如下表示：

数据位位置1234567891011121314151617181920...编码后数据位置p1p2d1p4d2d3d4p8d5d6d7d8d9d10d11p16d12d13d14d15奇偶校验位
覆盖率p1X X X X X X X X X X p2 XX XX XX XX XX p4 XXXX XXXX Xp8 XXXXXXXX p16 XXXXX

观察上表可发现一个比较直观的规律：第i个检验位是第2^i-1位，从该位开始，检验2^i-1位，跳过2^i-1位……依次类推。例如上表中第3个检验位p4从第2^3-1=4位开始，检验4、5、6、7共4位，然后跳过8、9、10、11共4位，再检验12、13、14、15共4位……

例子[编辑]

对11000010进行汉明编码，求编码后的码字。

1. 列出表格，从左往右（或从右往左）填入数字，但2的次方的位置不填。

位置1234567891011121314数据 1 100 0010

2. 把数据行有1的列的位置写为二进制。

位置1234567891011121314数据 1 100 0010 二进制 0011 0101 1011

3. 收集所有二进制数字，求异或。 $0011 \oplus 0101 \oplus 1011 =1101$

4. 把1101依次填入表格中2的次方的位置（低位在左）。

位置1234567891011121314数据 1 100 0010 二进制 0011 0101 1011 校验10 1 1

5. 所以编码后的码字是101110010010。

带附加奇偶校验码的汉明码 (SECDED)[编辑]

汉明(7,4)码[编辑]

Graphical depiction of the 4 data bits and 3 parity bits and which parity bits apply to which data bits

主条目：汉明(7,4)码

1950年，汉明介绍了(7,4)代码。其编码由4数据比特到7位，增加三个奇偶校验码。汉明(7,4)可以检测并纠正单比特错误，且也能检测双比特错误。

创建奇偶检验矩阵[编辑]

矩阵 $\mathbf{G} := \begin{pmatrix}I_k | -A^T \\\end{pmatrix}$ 被称为(标准)生成矩阵线性(n,k)码。

和 $\mathbf{H} := \begin{pmatrix}A | I_{n-k} \\\end{pmatrix}$ 被称为奇偶检验矩阵。

编码[编辑]

示例

从上述矩阵我们有2^k=2⁴=16码词。

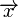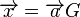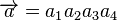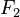二进制码 $\overrightarrow{x}$ 的码词可以从 $\overrightarrow{x}=\overrightarrow{a}G$ 得到。对 $\overrightarrow{a}=a_1a_2a_3a_4$ 和 $a_i$ 存在 $F_2$ （一个只有0和1的二元域）。

故此码表即是所有4个三元组（k个三元组）。

因而，(1,0,1,1)编码为(0,1,1,0,0,1,1).

汉明(8,4)码[编辑]

The same (7,4) example from above with an extra parity bit

汉明(7,4)码可以很容易地编码为一个(8,4)码，通过在(7,4)编码词（参见汉明(7,4)码）上附加一个额外的奇偶位。

这可以用下面修正的矩阵相加：

$\mathbf{G} := \begin{pmatrix}1 & 1 & 1 & 0 & 0 & 0 & 0 & 1\\1 & 0 & 0 & 1 & 1 & 0 & 0 & 1\\0 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\1 & 1 & 0 & 1 & 0 & 0 & 1 & 0\end{pmatrix}_{8,4}$

和

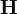$\mathbf{H} :=\begin{pmatrix}1 & 0 & 1 & 0 & 1 & 0 & 1 & 0\\0 & 1 & 1 & 0 & 0 & 1 & 1 & 0\\0 & 0 & 0 & 1 & 1 & 1 & 1 & 0\\1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\end{pmatrix}_{4,8}.$

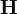注意， $\mathbf{H}$ 并非用标准形式表示。为了得到 $\mathbf{G}$ ，原子行操作能够被用来获得一个等价的矩阵对陈形式的 $\mathbf{H}$ ：

$\mathbf{H} =\left(\left.\begin{array}{cccc}0 & 1 & 1 & 1\\1 & 0 & 1 & 1\\1 & 1 & 0 & 1\\1 & 1 & 1 & 0\end{array}\right|\begin{array}{cccc}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{array}\right)_{4,8}.$

========================================================文二===================================================

以下内容摘自笔者即将出版的最新著作《深入理解计算机网络》一书。本书将于12月底出版上市，敬请留意！！

本书原始目录参见此文：http://winda.blog.51cto.com/55153/1063878

5.3.6 海明纠错码

海明码（Hamming Code）是一个可以有多个校验位，具有检测并纠正一位错误代码的纠错码，所以它也仅用于信道特性比较好的环境中，如以太局域网中，因为如果信道特性不好的情况下，出现的错误通常不是一位。

海明码的检错、纠错基本思想是将有效信息按某种规律分成若干组，每组安排一个校验位进行奇偶性测试，然后产生多位检测信息，并从中得出具体的出错位置，最后通过对错误位取反（也是原来是1就变成0，原来是0就变成1）来将其纠正。

要采用海明码纠错，需要按以下步骤来进行：计算校验位数→确定校验码位置→确定校验码→实现校验和纠错。下面来具体介绍这几个步骤。本文先介绍除最后一个步骤的其它几个步骤。

1. 计算校验位数

要使用海明码纠错，首先就要确定发送的数据所需要要的校验码（也就是“海明码”）位数（也称“校验码长度”）。它是这样的规定的：假设用N表示添加了校验码位后整个信息的二进制位数，用K代表其中有效信息位数，r表示添加的校验码位，它们之间的关系应满足：N=K＋r≤2^r－1。

如K=5，则要求2^r-r≥5+1=6，根据计算可以得知r的最小值为4，也就是要校验5位信息码，则要插入4位校验码。如果信息码是8位，则要求2^r-r≥8+1=9，根据计算可以得知r的最小值也为4。根据经验总结，得出信息码和校验码位数之间的关系如表5-1所示。

表5-1 信息码位数与校验码位数之间的关系

信息码位数

2~4

5~11

12~26

27~57

58~120

121~247

校验码位数

2．确定校验码位置

上一步我们确定了对应信息中要插入的校验码位数，但这还不够，因为这些校验码不是直接附加在信息码的前面、后面或中间的，而是分开插入到不同的位置。但不用担心，校验码的位置很容易确定的，那就是校验码必须是在2ⁿ次方位置，如第1、2、4、8、16、32，……位（对应2⁰、2¹、2²、2³、2⁴、2⁵，……，是从最左边的位数起的），这样一来就知道了信息码的分布位置，也就是非2ⁿ次方位置，如第3、5、6、7、9、10、11、12、13，……位（是从最左边的位数起的）。

举一个例子，假设现有一个8位信息码，即b1、b2、b3、b4、b5、b6、b7、b8，由表5-1得知，它需要插入4位校验码，即p1、p2、p3、p4，也就是整个经过编码后的数据码（称之为“码字”）共有12位。根据以上介绍的校验码位置分布规则可以得出，这12位编码后的数据就是p1、p2、b1、p3、b2、b3、b4、p4、b5、b6、b7、b8。

现假设原来的8位信息码为10011101，因现在还没有求出各位校验码值，现在这些校验码位都用“？”表示，最终的码字为：？？1？001？1101。

3. 确定校验码

经过前面的两步，我们已经确定了所需的校验码位数和这些校验码的插入位置，但这还不够，还得确定各个校验码值。这些校验码的值不是随意的，每个校验位的值代表了代码字中部分数据位的奇偶性（最终要根据是采用奇校验，还是偶校验来确定），其所在位置决定了要校验的比特位序列。总的原则是：第i位校验码从当前位开始，每次连续校验i（这里是数值i，不是第i位，下同）位后再跳过i位，然后再连续校验i位，再跳过i位，以此类推。最后根据所采用的是奇校验，还是偶校验即可得出第i位校验码的值。

1）计算方法

校验码的具体计算方法如下：

p1（第1个校验位，也是整个码字的第1位）的校验规则是：从当前位数起，校验1位，然后跳过1位，再校验1位，再跳过1位，……。这样就可得出p1校验码位可以校验的码字位包括：第1位（也就是p1本身）、第3位、第5位、第7位、第9位、第11位、第13位、第15位，……。然后根据所采用的是奇校验，还是偶校验，最终可以确定该校验位的值。

p2（第2个校验位，也是整个码字的第2位）的校验规则是：从当前位数起，连续校验2位，然后跳过2位，再连续校验2位，再跳过2位，……。这样就可得出p2校验码位可以校验的码字位包括：第2位（也就是p2本身）、第3位，第6位、第7位，第10位、第11位，第14位、第15位，……。同样根据所采用的是奇校验，还是偶校验，最终可以确定该校验位的值。

p3（第3个校验位，也是整个码字的第4位）的校验规则是：从当前位数起，连续校验4位，然后跳过4位，再连续校验4位，再跳过4位，……。这样就可得出p4校验码位可以校验的码字位包括：第4位（也就是p4本身）、第5位、第6位、第7位，第12位、第13位、第14位、第15位，第20位、第21位、第22位、第23位，……。同样根据所采用的是奇校验，还是偶校验，最终可以确定该校验位的值。

p4（第4个校验位，也是整个码字的第8位）的校验规则是：从当前位数起，连续校验8位，然后跳过8位，再连续校验8位，再跳过8位，……。这样就可得出p4校验码位可以校验的码字位包括：第8位（也就是p4本身）、第9位、第10位、第11位、第12位、第13位、第14位、第15位，第24位、第25位、第26位、第27位、第28位、第29位、第30位、第31位，……。同样根据所采用的是奇校验，还是偶校验，最终可以确定该校验位的值。

……

我们把以上这些校验码所校验的位分成对应的组，它们在接收端的校验结果（通过对各校验位进行逻辑“异或运算”得出）对应表示为G1、G2、G3、G4，……，正常情况下均为0。

2）校验码计算示例

同样举上面的例子来说明，码字为？？1？001？1101。

先求第1个“？”（也就是p1，第1位）的值，因为整个码字长度为12（包括信息码长和校验码长），所以可以得出本示例中p1校验码校验的位数是1、3、5、7、9、11共6位。这6位中除了第1位（也就是p1位）不能确定外，其余5位的值都是已知的，分别为：1、0、1、1、0。现假设采用的是偶校验（也就是要求整个被校验的位中的“1”的个数为偶数），从已知的5位码值可知，已有3个“1”，所以此时p1位校验码的值必须为“1”，得出p1=1。

再求第2个“？”（也就是p2，第2位）的值，根据以上规则可以很快得出本示例中p2校验码校验的位数是2、3、6、7、10、11，也是一共6位。这6位中除了第2位（也就是p2位）不能确定外，其余5位的值都是已知的，分别为：1、0、1、1、0。现假设采用的是偶校验，从已知的5位码值可知，也已有3个“1”，所以此时p2位校验码的值必须为“1”，得出p2=1。

再求第3个“？”（也就是p3，第4位）的值，根据以上规则可以很快得出本示例中p3校验码校验的位数是4、5、6、7、12，一共5位。这5位中除了第4位（也就是p3位）不能确定外，其余4位的值都是已知的，分别为：0、0、1、1。现假设采用的是偶校验，从已知的4位码值可知，也已有2个“1”，所以此时p2位校验码的值必须为“0”，得出p3=0。

最后求第4个“？”（也就是p4，第8位）的值，根据以上规则可以很快得出本示例中p4校验码校验的位数是8、9、10、11、12（本来是可以连续校验8位的，但本示例的码字后面的长度没有这么多位，所以只校验到第12位止），也是一共5位。这5位中除了第8位（也就是p4位）不能确定外，其余4位的值都是已知的，分别为：1、1、0、1。现假设采用的是偶校验，从已知的4位码值可知，已有3个“1”，所以此时p2位校验码的值必须为“1”，得出p4=1。

最后就可以得出整个码字的各个二进制值码字为：111000111101（带阴影的4位就是校验码）。

. 实现校验和纠错

虽然上一步已把各位校验码求出来了，但是如何实现检测出哪一位在传输过程中出了差错呢？（海明码也只能检测并纠正一位错误）它又是如何实现对错误的位进行纠正呢？其实最关键的原因就是海明码是一个多重校验码，也就是码字中的信息码位同时被多个校验码进行校验，然后通过这些码位对不同校验码的联动影响最终可以找出是哪一位出错了。

1）海明码的差错检测

现假设整个码字一共是18位，根据表5-1可以很快得出，其中有5位是校验码，再根据本节前面介绍的校验码校验规则可以很快得出各校验码所校验的码字位，如表5-2所示。

表5-2 各校验码校验的码位对照表

从表中可以得出以下两个规律：

l 所有校验码所在的位是只由对应的校验码进行校验，如第1位（只由p1校验）、第2位（只由p2校验）、第4位（只由p3校验）、第8位（只由p4校验）、第16位（只由p5校验），……。也就是这些位如果发生了差错，影响的只是对应的校验码的校验结果，不会影响其它校验码的校验结果。这点很重要，如果最终发现只是一个校验组中的校验结果不符，则直接可以知道是对应校验组中的校验码在传输过程中出现了差错。

l 所有信息码位均被至少两个校验码进行了校验，也就是至少校验了两次。查看对应的是哪两组校验结果不符，然后根据表5-2就可以很快确定是哪位信息码在传输过程中出了差错。

海明码校验的方式就是各校验码对它所校验的位组进行“异或运算”，即：

G1=p1⊕b1⊕b2⊕b4⊕b5⊕……

G2=p2⊕b1⊕b3⊕b4⊕b6⊕b7⊕b10⊕b11⊕……

G3= p3⊕b2⊕b3⊕b4⊕b8⊕b9⊕b10⊕b11⊕……

G4= p4⊕b5⊕b6⊕b7⊕b8⊕b9⊕b10⊕b11⊕……

G5= p5⊕b12⊕b13⊕b14⊕b15⊕b16⊕b17⊕b18⊕b19⊕b20⊕b21⊕b11⊕b23⊕b24⊕b25⊕b26⊕……

正常情况下（也就是整个码字不发生差错的情况下），在采用偶校验时，各校验组通过异或运算后的校验结果均应该是为0，也就是前面所说的G1、G2、G3、G4，……均为0，因为此时1为偶数个，进行异或运算后就是0；而采用奇校验时，各组校验结果均应是为1。

现在举一个例子来说明，假设传输的海明码为111000111101（一共12位，带阴影的4位就是校验码），从中可以知道它有四个校验组：G1、G2、G3、G4，然而到达接收端经过校验后发现只有G4=1（也就是只有这组校验结果不等于0），通过前面介绍的校验规律可以很快地发现是G4校验组中的p4校位码（也就是整个码字中的第8位）错了（因为只有一组校验结果出现差错时，则肯定只是对应的校验位出了差错），也就是最终的码字变成了：111000001101。

再假设G3、G4两个校验值都不为0，也就是都等于1。通过表5-2中比较G3、G4两个校验组（注意本示例中码字长度一共才12位，只需要比较前12位）中共同校验的码位可是以很快发现是b8，也就是第12位出现了差错，也就是最终的码字变成了：111000011100。

【经验之谈】在这里一定要注意，最终有多少个校验组出现差错也不是随意的，一定要结合实际传输的码字长度来考虑。如上例是一共12位，如果换成了是16位的码字，且当b9位出现差错时，则G1、G3、G4一定会同时出现错误，因为b9这个位是三个校验组同时校验的，只要它一出错，肯定会同时影响这三个校验组的值。同理，如果是b11位出现了差错，因为它同时受G1、G2、G3、G4四个校验组校验，所以这四个校验组结果都将出现错误。

2）海明码的差错纠正

检测出了是哪位差错还不够，因为海明码具有纠正一位错误的能力，所以还需要完成纠错过程。这个过程的原理比较简单，就是直接对错误的位进行取反，或者加“1”操作，使它的值由原来的“1”变成“0”，由原来的“0”变成“1”（因为二进制中每一位只能是这二者之一）。

以上就是海明码的整差错检测和差错纠正原理了，确实比单纯的奇偶校验码复杂些，但只要理清了思路，也还是比较简单的。

1 0