HDU3847 Trash Removal(凸包)
来源:互联网 发布:哈萨克歌软件 编辑:程序博客网 时间:2024/06/05 00:25
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3847
Trash Removal
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 635 Accepted Submission(s): 221
Special Judge
Problem Description
Allied Chute Manufacturers is a company that builds trash chutes. A trash chute is a hollow tube installed in buildings so that trash dropped in at the top will fall down and be collected in the basement. Designing trash chutes is actually highly nontrivial. Depending on what kind of trash people are expected to drop into them, the trash chute needs to have an appropriate size. And since the cost of manufacturing a trash chute is proportional to its size, the company always would like to build a chute that is as small as possible. Choosing the right size can be tough though.
We will consider a 2-dimensional simplification of the chute design problem. A trash chute points straight down and has a constant width. Objects that will be dropped into the trash chute are modeled as polygons. Before an object is dropped into the chute it can be rotated so as to provide an optimal fit. Once dropped, it will travel on a straight path downwards and will not rotate in flight. The following figure shows how an object is first rotated so it fits into the trash chute.
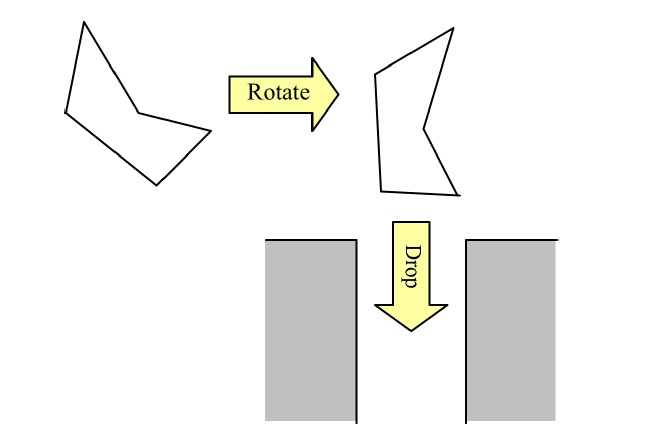
Your task is to compute the smallest chute width that will allow a given polygon to pass through.
We will consider a 2-dimensional simplification of the chute design problem. A trash chute points straight down and has a constant width. Objects that will be dropped into the trash chute are modeled as polygons. Before an object is dropped into the chute it can be rotated so as to provide an optimal fit. Once dropped, it will travel on a straight path downwards and will not rotate in flight. The following figure shows how an object is first rotated so it fits into the trash chute.

Your task is to compute the smallest chute width that will allow a given polygon to pass through.
Input
The input contains several test cases. Each test case starts with a line containing an integer n (3 <= n <= 100), the number of points in the polygon that models the trash item.
The next n lines then contain pairs of integers xi and yi (0 <= xi, yi <= 10^4), giving the coordinates of the polygon vertices in order. All points in one test case are guaranteed to be mutually distinct and the polygon sides will never intersect. (Technically, there is one inevitable exception of two neighboring sides sharing their common vertex. Of course, this is not considered an intersection.)
The last test case is followed by a line containing a single zero.
The next n lines then contain pairs of integers xi and yi (0 <= xi, yi <= 10^4), giving the coordinates of the polygon vertices in order. All points in one test case are guaranteed to be mutually distinct and the polygon sides will never intersect. (Technically, there is one inevitable exception of two neighboring sides sharing their common vertex. Of course, this is not considered an intersection.)
The last test case is followed by a line containing a single zero.
Output
For each test case, display its case number followed by the width of the smallest trash chute through which it can be dropped. Display the minimum width with exactly two digits to the right of the decimal point, rounding up to the nearest multiple of 1/100. Answers within 1/100 of the correct rounded answer will be accepted.
Sample Input
30 03 00 440 1010 020 1010 200
Sample Output
Case 1: 2.40Case 2: 14.15
题意:有一个多边形的垃圾和一个通道,可以任意旋转多边形,问通道的直径最小需要多少才能让多边形通过。
多边形的形状是没有价值的,所以直接求出这些顶点的凸包。
然后对于凸包的每条边,求出每个点到这条边的最大距离,再求出这些最大距离中的最小距离。
最后注意输出格式,2位小数,向上进位。
#include <iostream>#include <cstdio>#include <cstring>#include <string>#include <algorithm>#include <cmath>using namespace std;#define INF 0x3f3f3f3f#define eps 1e-8struct point{ double x,y; point(){} point(double _x,double _y) { x=_x;y=_y; } point operator - (const point &b) const { return point(x-b.x,y-b.y); } bool operator < (const point &b) const { return x<b.x||x==b.x&&y<b.y; } double len() { return sqrt(x*x+y*y); }}res[105],p[105];int n;int dcmp(double x){ return (x>eps)-(x<-eps);}double dis(point a,point b){ return (a-b).len();}double cross(point a,point b){ return a.x*b.y-b.x*a.y;}double ptoline(point p,point a,point b)//点到直线距离{ return (fabs(cross(p-a,b-a))/dis(a,b));}int andrew()//求出凸包{ sort(p,p+n); int m=0; for (int i=0;i<n;i++) { while (m>1&&cross(res[m-1]-res[m-2],p[i]-res[m-2])<0) --m; res[m++]=p[i]; } int k=m; for (int i=n-2;i>=0;--i) { while (m>k&&cross(res[m-1]-res[m-2],p[i]-res[m-2])<0) --m; res[m++]=p[i]; } if (m>1) --m; return m;}int main(){ int ca=0; while (scanf("%d",&n)!=EOF&&n!=0) { for (int i=0;i<n;i++) { scanf("%lf%lf",&p[i].x,&p[i].y); } int m=andrew(); res[m]=res[0]; double mi=INF; for (int i=0;i<m;i++) { double ma=-1; for (int j=0;j<n;j++)//对每条边求出最大距离 { double tmp=ptoline(p[j],res[i],res[i+1]); //if (dcmp(tmp)==0) continue; if (dcmp(tmp-ma)>0) ma=tmp; } if (dcmp(ma-mi)<0) mi=ma;//求出最大距离中的最小值 } mi=ceil(mi*100)/100.0;//控制输出 printf("Case %d: %.2lf\n",++ca,mi); } return 0;} 0 0
- HDU3847 Trash Removal(凸包)
- HDU3847——Trash Removal(凸包,枚举)
- hdu 3847 Trash Removal 2011WorldFinal 凸包
- 凸包Graham扫描法->HDU3847
- uva 1111 - Trash Removal
- hdu 3847 Trash Removal
- hdu 3847 Trash Removal(简单几何)
- Trash Removal uva1111/uvalive5138 World Final 2011 K 计算几何
- trash
- Linux/Unix回收站(trash)
- 引用去除(Quote Removal)
- POJ 3183 Stump Removal(简单题)
- POJ 3183 Stump Removal(水~)
- Ural 1076 Trash (二分图最佳完美匹配)
- Mac回收Trash(废纸篓)空间问题
- URAL1076.Trash(垃圾)——最佳匹配
- 1076. Trash(KM算法 二分最佳完美匹配)
- ubuntu trash
- fsdfdsfsdf
- (经过试验)我的驱动和程序共享内存代码
- android 主线程和子线程之间的消息传递
- UVa -- 10324 Zeros and Ones
- jquery error: 200
- HDU3847 Trash Removal(凸包)
- windows游戏编程<七> 创建WIN32一个HelloWOrld程序
- ffmpeg+sdl2.0做一个简单的音频播放器
- Transfer postgres database to another server - backup and restore
- Spring 基础教程之五:AOP编程介绍
- URL和URI的区别和联系
- 绝对路径和相对路径的区别
- 10Servlet-filter 实例
- CSDN处女篇


