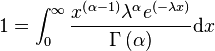Gamma 函数
来源:互联网 发布:手机如何修改淘宝差评 编辑:程序博客网 时间:2024/05/08 05:38
转自:
http://blog.sina.com.cn/s/blog_6c17a3a00100o4xx.html
Γ函数
维基百科,自由的百科全书
跳转到: 导航, 搜索
汉漢▼
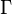 函数,也叫做伽玛函数(Gamma函数),是阶乘函数在实数与复数上的扩展。对于实数部份为正的复数z,伽玛函数定义为:
函数,也叫做伽玛函数(Gamma函数),是阶乘函数在实数与复数上的扩展。对于实数部份为正的复数z,伽玛函数定义为:
此定义可以用解析开拓原理拓展到整个复数域上,非正整数除外。
如果n为正整数,则伽玛函数定义为:
- Γ(n) = (n − 1)!,
这显示了它与阶乘函数的联系。可见,伽玛函数将n拓展到了实数与复数域上。
在概率论中常见此函数,在组合数学中也常见。
目录
[隐藏]- 1 定义
- 2 无穷乘积
- 3 Gamma积分
- 4 递推公式
- 4.1 递推公式的推导
- 5 重要性质
- 6 特殊值
- 7 导数
- 8 复数值
- 9 斯特灵公式
- 10 解析延拓
- 11 参见
- 12 外部链接
定义
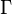 函数可以通过欧拉(Euler)第二类积分定义:
函数可以通过欧拉(Euler)第二类积分定义:
对复数 ,我们要求Re(z) > 0。
,我们要求Re(z) > 0。
Γ函数还可以通过对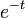 做泰勒展开,解析延拓到整个复平面:
做泰勒展开,解析延拓到整个复平面: 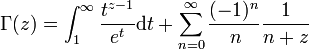
这样定义的Γ函数在全平面除了 以外的地方解析。
以外的地方解析。
Γ函数也可以用无穷乘积的方式表示:

这样定义的Γ函数在全平面解析
无穷乘积
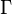 函数可以用无穷乘积表示:
函数可以用无穷乘积表示:
其中 是欧拉-马歇罗尼常数。
是欧拉-马歇罗尼常数。
Gamma积分

递推公式
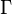 函数的递推公式为: Γ(x + 1) = xΓ(x),
函数的递推公式为: Γ(x + 1) = xΓ(x),
对于正整数 ,有
,有
Γ(n + 1) = n!,
可以说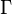 函数是阶乘的推广。
函数是阶乘的推广。
递推公式的推导

我们用分部积分法来计算这个积分:
![伽玛函数 \int_0^\infty e^{-x} x ^n dx = \left[\frac{-x^n}{e^x}\right]_0^\infty + n \int_0^\infty e^{-x} x ^{n - 1} {\rm{d}} x](http://upload.wikimedia.org/math/0/9/3/093ed6f1ed6fdddd5aa183d67a63f320.png)
当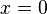 时,
时, 。当
。当 趋于无穷大时,根据洛必达法则,有:
趋于无穷大时,根据洛必达法则,有:
 .
.
因此第一项![伽玛函数 \left[\frac{-x^n}{e^x}\right]_0^\infty](http://upload.wikimedia.org/math/d/7/7/d774d2bbd5332fbb86b57635227fc596.png) 变成了零,所以:
变成了零,所以:
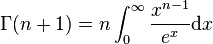
等式的右面正好是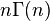 。因此,递推公式为:
。因此,递推公式为:
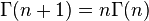 。
。
0 0
- Gamma函数
- Gamma函数
- Gamma 函数
- 神奇的Gamma函数
- 神奇的Gamma函数
- gamma曲线函数
- Gamma 函数及其应用
- 用java计算gamma函数
- Gamma函数相关matlab代码
- Gamma 分布函数可加性证明
- gamma
- gamma
- Gamma
- gamma
- 单位阶跃函数,δ函数, gamma函数
- LDA-math-神奇的Gamma函数
- LDA-math-神奇的Gamma函数
- 转帖:LDA-math-神奇的Gamma函数
- 听课笔记(第六讲): 归纳理论(台大机器学习)
- 听课笔记(第五讲): 学习的可行性分析(一些概念和思想) (台湾国立大学机器学习基石)
- powerdesigner 通过jdbc连接数据库mysql 逆向工程带图详解
- 第一个Linux驱动
- IT运维管理发展
- Gamma 函数
- 对IT运维的一些看法
- Visual Studio + VA 常用快捷键
- 文本与二进制方式打开文件的区别
- 程序员成长攻略
- 黑马程序员 Java面向对象——正则表达式
- jQuery UI Autocomplete 体验分享
- 黑马程序员 Java面向对象——JDK 1.5新特性
- 黑马程序员 Java面向对象——交通灯管理系统