Floyd算法

三次循环解决任意两点间的最短路径的算法，可以处理有向图或负权值的最短路径问题，同时也被用于计算有向图的传递闭包

设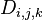为从到的只以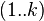集合中的节点为中间節点的最短路径的长度。

1. 若最短路径经过点k，则；
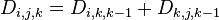2. 若最短路径不经过点k，则。

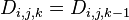因此，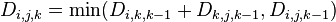

初始化Dis[i][i]=0;Dis[i][j]=INF; 将图中的边存入Dis[i][j]
for ( int k= 1; k<= n; k++ )   // n为节点个数
{
    for ( int i= 1; i <=n; i++ )
    {
        for ( int j = 1; j <=n; j++ )
        {
            if ( Dis[i][k] + Dis[k][j] < Dis[i][j] )   // 找到更短路径
                Dis[i][j] = Dis[i][k] + Dis[k][j];
        }
    }
}

真正的Floyd算法是一种基于DP(Dynamic Programming)的最短路径算法。

  设图G中n 个顶点的编号为1到n。令c [i, j, k]表示从i 到j 的最短路径的长度，其中k 表示该路径中的最大顶点，也就是说c[i,j,k]这条最短路径所通过的中间顶点最大不超过k。因此，如果G中包含边<i, j>，则c[i, j, 0] =边<i, j> 的长度；若i= j ，则c[i,j,0]=0；如果G中不包含边<i, j>，则c (i, j, 0)= +∞。c[i, j, n] 则是从i 到j 的最短路径的长度。

  对于任意的k>0，通过分析可以得到：中间顶点不超过k 的i 到j 的最短路径有两种可能：该路径含或不含中间顶点k。若不含，则该路径长度应为c[i, j, k-1]，否则长度为 c[i, k, k-1] +c [k, j, k-1]。c[i, j, k]可取两者中的最小值。

  状态转移方程：c[i, j, k]=min{c[i, j, k-1], c [i, k, k-1]+c [k, j, k-1]}，k＞0。

  这样，问题便具有了最优子结构性质，可以用动态规划方法来求解。

1. void floyd_dp(){  
2. 18     int i,j,k;  
3. 19     for(i=1;i<=n;i++)  
4. 20         for(j=1;j<=n;j++)  
5. 21             dist[i][j][0]=map[i][j];  
6. 22     for(k=1;k<=n;k++)  
7. 23         for(i=1;i<=n;i++)  
8. 24             for(j=1;j<=n;j++){  
9. 25                 dist[i][j][k]=dist[i][j][k-1];  
10. 26                 if(dist[i][k][k-1]+dist[k][j][k-1]<dist[i][j][k])  
11. 27                     dist[i][j][k]=dist[i][k][k-1]+dist[k][j][k-1];  
12. 28             }  
13. 29 }