MAT-中国剩余定理

来源：互联网发布：淘宝服装质检编辑：程序博客网时间：2024/05/01 04:54

中国剩余定理

中国剩余定理，又称孙子定理，数论中的重要定理，中国古代用于求解一次同余组的方法。问题的原文出自<孙子算经>,描述如下：

"有物不知其数，三个一数余二，五个一数余三，七个一数又余二，问该物总数几何？"

意思是有一个数X，除以3余2，除以5余3，除以7余2，求该数X，当然，<孙子算经>也给出了解题的方法：

"三三数之，取数七十，与余数二相乘；五五数之，取数二十一，与余数三相乘；七七数之，取数十五，与余数二相乘。将诸乘积相加，然后减去一百零五的倍数。"

按照上面的思路，我们分别取数70,21,15,并分别乘上相应的值，得公式X=70*2+21*3+15*2-105*k.这里k为任意整数,假设k=1，根据该公式计算得X=140+63+30-105=128.

带到问题验证下:128%3=2 , 128%5=3, 128%7=2. k=2时，解得X=23，可以验证同样符合题意。

那么我们关心的是，这组简单的公式如何得到？

这里有三个关键数70,21,15，可以简单使用公式描述他们的性质：

70%3=1,70%5=0,70%7=0;

21%3=0,21%5=1,21%7=0;

15%3=0,15%5=0,15%7=1;

我们发现它们的性质很简单，但也有趣，它们分别对3,5,7也就是我们的除数mod(取余)余1，对其他数都能够被整除。同时，我们对70,21,15这三个数乘上2,3,2,是因为数X

对3,5,7的余数分别为2,3,2. 如70，其实是要找余2的，但只要找到了余1的再乘2即余2了,最后的105代表3,5,7的最小公倍数，即105=3*5*7.

总之，孙子问题的解法，是找出三个关键数70，21，15。解法的意思就是用70乘（3除所得的余数），21乘（5除所得的余数），15乘（7除所得的余数），然后总加起来，减去105的倍数就是答案。

简单解释

假设任意三个数a,b,c,数X对他们的余数分别为m1,m2,m3,分别找出能被两个数整除，而满足被第三个整数整除余1的最小数。即

k1%a=1,k1%b=0,k1%c=0

k2%a=0,k2%b=1,k2%c=0

k3%a=0,k3%b=0,k3%c=1

这里，令T1，T2，T3分别为：

T1=k1*m1;(满足T1%a=m1,T1%b=T1%c=0)

T2=k2*m2;(满足T2%b=m1,T2%a=T2%c=0)

T3=k3*m3;(满足T3%c=m3,T3%a=T3%b=0)

设T‘ = T1+T2+T3 ，则T’显然能够满足题目，又Q=a*b*c能同时整除a,b,c，固X=T‘+tQ(t为任意整数)满足题目要求的解。

定理的通用形式：

用现代数学语言来说明的话，中国剩余定理可以描述为下面的一次线性同余方程组:

中国剩余定理说明：假设m1,m2,....mn两两互质,对任意的整数a1,a2,a3.....an，方程(S)有解，并且通解可以用如下方式构造得到:

1.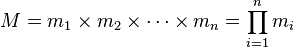 $M = m_1 \times m_2 \times \cdots \times m_n = \prod_{i=1}^n m_i$ (m1,m2...mn的乘积)，并设 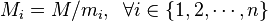$M_i = M/m_i, \; \; \forall i \in \{1, 2, \cdots , n\}$ 是除了 $m i$ 以外的 $n - 1$ 个整数的乘积。

2.设 $t_i = M_i^{-1}$ 为 $M_i$ 模 $m_i$ 的数论倒数： $t_i M_i \equiv 1 \pmod {m_i}, \; \; \forall i \in \{1, 2, \cdots , n\}.$

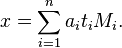
3.方程组 $(S)$ 的通解形式为： $x = a_1 t_1 M_1 + a_2 t_2 M_2 + \cdots + a_n t_n M_n + k M= k M + \sum_{i=1}^n a_i t_i M_i, \quad k \in \mathbb{Z}.$ 在模 $M$ 的意义下，方程组 $(S)$ 只有一个解： $x = \sum_{i=1}^n a_i t_i M_i.$

注：第2步中，ti为Mi模mi的数论倒数，也就是求解关键数的关键一步，在上述问题中，例如70=2*5*7，即2为这里的t值。

证明

从假设可知，对任何 $i \in \{1, 2, \cdots , n\}$ ，由于 $\forall j \in \{1, 2, \cdots , n\}, \; j\neq i, \; \; \operatorname{gcd}(m_i, m_j) = 1$ ，所以 $\operatorname{gcd}(m_i, M_i) = 1.$ 即mi,mj互质，最大公约数为1,这说明存在整数 $t_i$ 使得 $t_i M_i \equiv 1 \pmod {m_i}.$ （<MAT-欧几里得与拓展欧几里得算法>一篇已证明）.

$a_i t_i M_i \equiv a_i \cdot 1 \equiv a_i \pmod {m_i},$

$\forall j \in \{1, 2, \cdots , n\}, \; j\neq i, \; \; a_i t_i M_i \equiv 0 \pmod {m_j}.$

注：类似说明简单解释中的T1%a=m1,T1%b=0,T1%c=0.

所以 $x = a_1 t_1 M_1 + a_2 t_2 M_2 + \cdots + a_n t_n M_n$ 满足：

$\forall i \in \{1, 2, \cdots , n\}, \; \; x = a_i t_i M_i + \sum_{j \neq i} a_j t_j M_j \equiv a_i + \sum_{j \neq i} 0 \equiv a_i \pmod {m_i}.$ (这里的x同T')

这说明x就是方程组S的一个解。而所以方程组 $(S)$ 的任何两个解之间必然相差 $M$ 的整数倍，由于 $x = a_1 t_1 M_1 + a_2 t_2 M_2 + \cdots + a_n t_n M_n$ 是一个解，同时所有形式为： $a_1 t_1 M_1 + a_2 t_2 M_2 + \cdots + a_n t_n M_n + k M= k M + \sum_{i=1}^n a_i t_i M_i, \quad k \in \mathbb{Z}$ 的整数也是方程组 $(S)$ 的解。所以方程组 $(S)$ 所有的解的集合就是：

$\{k M + \sum_{i=1}^n a_i t_i M_i \; ; \quad k \in \mathbb{Z} \}.$

0 0