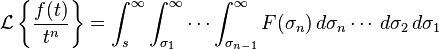单边正弦信号拉斯变换 matlab
来源:互联网 发布:java treemap 编辑:程序博客网 时间:2024/04/30 15:38
单边正弦信号拉氏变换
拉普拉斯变换:拉普拉斯变换是应用数学中常用的一种积分变换,又名拉氏转换,其符号为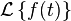 。拉氏变换是一个线性变换,可将一个有引数实数t(t ≥ 0)的函数转换为一个引数为复数s的函数。
。拉氏变换是一个线性变换,可将一个有引数实数t(t ≥ 0)的函数转换为一个引数为复数s的函数。
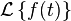 。拉氏变换是一个线性变换,可将一个有引数实数t(t ≥ 0)的函数转换为一个引数为复数s的函数。
。拉氏变换是一个线性变换,可将一个有引数实数t(t ≥ 0)的函数转换为一个引数为复数s的函数。应用:有些情形下一个实变量函数在实数域中进行一些运算并不容易,但若将实变量函数作拉普拉斯变换,并在复数域中作各种运算,再将运算结果作拉普拉斯反变换来求得实数域中的相应结果,往往在计算上容易得多。拉普拉斯变换的这种运算步骤对于求解线性微分方程尤为有效,它可把微分方程化为容易求解的代数方程来处理,从而使计算简化。
基本定义[编辑]
如果定义:
 是一个关于
是一个关于 的函数,使得当
的函数,使得当 时候,
时候, ;
; 是一个复变量;
是一个复变量; 是一个运算符号,它代表对其对象进行拉普拉斯积分
是一个运算符号,它代表对其对象进行拉普拉斯积分 ;
; 是
是 的拉普拉斯变换结果。
的拉普拉斯变换结果。
则 的拉普拉斯变换由下列式子给出:
的拉普拉斯变换由下列式子给出:

拉普拉斯变换的基本性质[编辑]
- 线性叠加
- 时域微分(单边拉普拉斯变换)
- s域微分
- s域积分
- 时域积分
- 初值定理
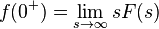 ,要求
,要求 为真分式,即分子的最高次小于分母的最高次,否则使用多项式除法将
为真分式,即分子的最高次小于分母的最高次,否则使用多项式除法将 分解
分解
- 终值定理
 ,要求
,要求 的所有极点都在左半复平面或原点为单极点。
的所有极点都在左半复平面或原点为单极点。- 终值定理的实用性在于它能预见到系统的长期表现,且避免部分分式展开。如果函数的极点在右半平面,那么系统的终值未定义(例如:
 或
或  )。
)。
 域平移
域平移
- 时域平移
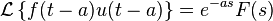

- 注:
 表示阶跃函数.
表示阶跃函数.
- 卷积
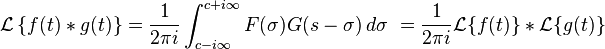 ,
, 是收敛区间的横坐标值,是一个实常数且大于所有
是收敛区间的横坐标值,是一个实常数且大于所有 的个别点的实部值。
的个别点的实部值。
- 下面给出一个例题:
例6-1:已知连续时间信号,求出该信号的拉普拉斯变换,并利用MATLAB绘制拉普拉斯变换的曲面图。
解:该信号的拉普拉斯变换为:
利用上面介绍的方法来绘制单边正弦信号拉普拉斯变换的曲面图,实现过程如下:
%绘制单边正弦信号拉普拉斯变换曲面图程序
注释: meshgrid() 用来产生 矩阵 s s 是一个复频域 a 为实部 b为 虚部
ones()函数将器全部变成1
mesh 函数可以画出曲面图 三维的
abs() 取绝对值
代码:
close all;a = -0.5:0.08:0.5;b = -1.99:0.08:1.99;[a,b] = meshgrid(a,b);d = ones(size(a));c = a +i*b;c = c.*c;c =c + d;c = 1./c;c = abs(c);mesh(a,b,c);surf(a,b,c);axis([-0.5,0.5,-2,2,0,15]);title('单边正弦信号拉斯变换曲线图');colormap(hsv);
运行结果:
0 0
- 单边正弦信号拉斯变换 matlab
- matlab实现信号的变换
- matlab实现信号的变换
- 编写MATLAB脚本产生正弦信号的mif文件
- 正弦信号、余弦信号与复指数信号(欧拉公式)
- 利用希尔伯特变换进行的单边带幅度调制matlab程序
- matlab-自控原理 拉氏变换
- 正弦信号的向量表示
- 信号傅立叶变换后实际频谱图(Matlab)
- DDS-正弦-SignalTap和MATLAB
- DDS-正弦-Modelsim和MATLAB
- 信号与系统2:正弦信号和指数信号
- 信号与系统2:正弦信号和指数信号
- 信号与系统学习(1)-正弦信号和指数信号
- 正弦函数及其FFT变换(一)
- 正弦函数及其FFT变换(二)
- 使用fftw3-3进行正弦变换
- 基于OpenCV的离散正弦变换
- Scons脚本注意事宜1
- Java学习笔记_24_Map接口
- VS2010 Entity Framework连接Mysql数据库中文乱码问题
- showModalDialog在父窗体和子窗体之间传值
- 创新实验室实习生每周工作总结【实习第八周】
- 单边正弦信号拉斯变换 matlab
- java中防止表单的重复提交
- ftk学习记(waitbox篇)
- 正则表达式入门精解
- 记第一届ACM讲堂
- 设置网卡混杂模式
- FZU 2165 Climb Stairs(DP)
- 监控Tomcat并启动
- WindowManager.LayoutParams(上)





![\mathcal{L}\{\,t^nf(t)\} = (-1)^nD_s^n[F(s)]](http://upload.wikimedia.org/math/f/7/5/f75194212391d819688d6d298bd219d0.png)