Dijkstra算法

From http://www.cnblogs.com/gzydn/archive/2009/07/09/1520019.html

 Dijkstra算法又称为单源最短路径，所谓单源是在一个有向图中，从一个顶点出发，求该顶点至所有可到达顶点的最短路径问题。 
      设G=（V，E）是一个有向图，V表示顶点，E表示边。它的每一条边（i，j）属于E，都有一个非负权W（I,j），在G中指定一个结点v0，要求把从v0到G的每一个接vj（vj属于V）的最短有向路径找出来（或者指出不存在）。
      Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离
基本思想是：
      设置一个顶点的集合s，并不断地扩充这个集合，一个顶点属于集合s当且仅当从源点到该点的路径已求出。开始时s中仅有源点，并且调整非s中点的最短路径长度，找当前最短路径点，将其加入到集合s，直到终点在s中。
基本步骤：
1、把所有结点分成两组：
      第一组：包括已经确定最短路径的结点；
      第二组：包括尚未确定最短路径的结点。
2、开始时，第一组只包含起点，第二组包含剩余的点；
3、用贪心的策略，按最短路径长度递增的顺序把第二组的结点加到第一组去，直到v0可达的所有结点都包含于第一组中。在这个过程中，不断更新最短路径，总保持从v0到第一组各结点的最短路径长度dist都不大于从v0到第二组任何结点的路径长度。
4、每个结点对应一个距离值，第一组结点对应的距离就是v0到此结点的最短路径长度，第二组结点对应的距离值就是v0由第一组结点到此结点的最短路径长度。
5、直到所有的顶点都扫描完毕（v0可达的所有结点都包含于第一组中），找到v0到其它各点的所有最短路径。

 动画演示：http://www.jcc.jx.cn/kejiandb/Dijkstra.swf

 如图：求0点到其他点的最短路径。

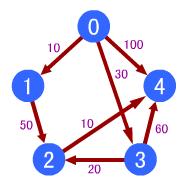
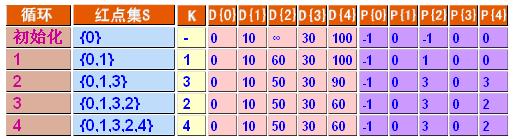
(1)开始时，s1={v0},s2={v1,v2,v3,v4}，v0到各点的最短路径是{0,10,&,30,100};
(2)在还未进入s1的顶点之中，最短路径为v1，因此s1={v0,v1},由于v1到v2有路径，因此v0到各点的最短路径更新为{0,10,60,30,100};
(3)在还未进入s1的顶点之中，最短路径为v3，因此s1={v0,v1,v3},由于v3到v2、v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,90}；
(4)在还未进入s1的顶点之中，最短路径为v2，因此s1={v0,v1,v3,v2},由于v2到v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,60};
数据结构：
(1)用一个二维数组a[i..j,i..j]来存储各点之间的距离，10000表示无通路：
(2)用数组dist[i..j]表示最短路径；
(3)用集合s表示找到最短路径的结点。 

from http://www.blogjava.net/javacap/archive/2007/09/07/143375.html

算法：

设G是带权图，图中的顶点多于一个，且所有的权都为正数。本算法确定从顶点S到G中其他各个顶点的距离和最短通路。在本算法中P表示带永久标记的顶点的集合。顶点A的前驱是P中的一个顶点，用来标记A。顶点U和V之间的边的权重用W（U，V）表示，如果U和V之间没有边，则记作W(U,V)=∞.

步骤1 （对S做标记）

      （a）将S标记为0，并使S没有前驱

      （b）令P={S}

步骤2 （对其他顶点作标记）

      将每个不在P中的顶点V标记为W(S,V)(可能是暂时的），并使V的前驱为S（可能是暂时的）

步骤3 （扩大P，修改标记）

     Repeat

     步骤3.1 （是另一个标记永久化）

                  把不在P中且带有最小标记的顶点U加入到P中去（如果这样的顶点有多个则任选其中一个）

    步骤3.2  （修改临时标记）

                对每个不在P中并且和U相邻的顶点X，把X的标记替换为下列这两者中的较小者：i)X的旧标记,ii)U上的标记与W（U，X）之和。如果X的标记改变了，则使U成为X的新前驱（可能是暂时的）

    Until P包含G中的每一个顶点

步骤4 （求出距离和最短通路）

   顶点Y上的标记是从S到Y的距离。如果Y上的标记是∞，那么从S到Y就没有通路，从而

没有最短通路；否则，按照下列序列的逆序使用顶点就构成从S到Y的一条最短通路：

Y，Y的前驱，Y的前驱的前驱，。。。。，直至S

 

 

证明：Dijkstra算法给出了从S到G的各个顶点的最短通路长度。

 

我们假设Ｇ中的每个顶点Ｖ都被赋予了一个标记L(V),它要么是一个数，要么是∞。假设P是G的顶点的集合，P包含S，满足：

1）如果V属于P，则L（V）是从S到V的最短通路的长度，并且存在这样的从S到V的最短通路：通路上的顶点都在P中

2）如果V不属于P，则L(V)是从S到V的满足下面限制的最短通路的长度：V是通路中唯一一个不属于P的顶点。

 

我们可以用归纳法证明Dijkstra算法中的P符合上述定义的集合：

1）当P中元素个数为1时，P对应算法中的第一步，P={S},显然满足。

2）假设P中元素个数为K时，P满足上述定义，下面看算法的的第三步，

   先找出不在P中且带有最小标记的顶点U，标记为L(U), 可以证明从S到U的最短通路中除U外不包含不属于P的元素。

因为若存在除U外其他顶点，则最短通路为SP1P2...PnQ1Q2...QnU(P1,P2..Pn属于P,Q1,Q2,...Qn不属于P),则由性质2）最短通路长度为L(Q1)+PATH(Q1,U)>L(U)

从而大于SP1P2..PnU的通路长度L(U)，不是最短通路，所以从S到U的最短通路中除U外不包含不属于P的元素，从而从S到U的最短通路长度由L(U)给出.

现把U加入P中构成P' ,显然P'满足性质1)。

取V不属于P',显然V也不属于P,那么从S到V的最短通路且满足除V外所有顶点都在P'中的通路有两种可能，i）包含U，ii）不包含U。

对i）SP1P2...PnUV=L(U)+W(U,V)

   ii)SP1P2..PnV=L(V)

显然二者中的最小给出了从S到V的最短通路且满足除V外所有顶点都在P'中的长度。

从而算法第三步给出的P'含K+1个元素且满足1),2)。

又归纳，命题得证！