hdu 1950
来源:互联网 发布:qq飞车改装数据最高 编辑:程序博客网 时间:2024/06/03 13:01
Problem Description
'Oh no, they've done it again', cries the chief designer at the Waferland chip factory. Once more the routing designers have screwed up completely, making the signals on the chip connecting the ports of two functional blocks cross each other all over the place. At this late stage of the process, it is too
expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without rossing each other, is imminent. Bearing in mind that there may be housands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task?
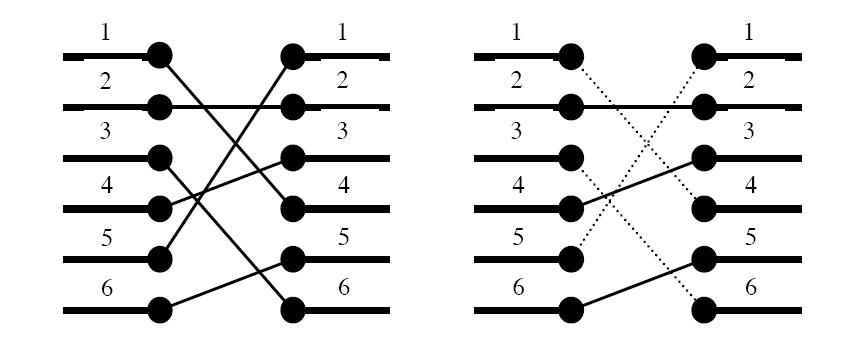
Figure 1. To the left: The two blocks' ports and their signal mapping (4,2,6,3,1,5). To the right: At most three signals may be routed on the silicon surface without crossing each other. The dashed signals must be bridged.
A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers in the range 1 to p, in which the i:th number pecifies which port on the right side should be connected to the i:th port on the left side.
Two signals cross if and only if the straight lines connecting the two ports of each pair do.
expensive to redo the routing. Instead, the engineers have to bridge the signals, using the third dimension, so that no two signals cross. However, bridging is a complicated operation, and thus it is desirable to bridge as few signals as possible. The call for a computer program that finds the maximum number of signals which may be connected on the silicon surface without rossing each other, is imminent. Bearing in mind that there may be housands of signal ports at the boundary of a functional block, the problem asks quite a lot of the programmer. Are you up to the task?

Figure 1. To the left: The two blocks' ports and their signal mapping (4,2,6,3,1,5). To the right: At most three signals may be routed on the silicon surface without crossing each other. The dashed signals must be bridged.
A typical situation is schematically depicted in figure 1. The ports of the two functional blocks are numbered from 1 to p, from top to bottom. The signal mapping is described by a permutation of the numbers 1 to p in the form of a list of p unique numbers in the range 1 to p, in which the i:th number pecifies which port on the right side should be connected to the i:th port on the left side.
Two signals cross if and only if the straight lines connecting the two ports of each pair do.
Input
On the first line of the input, there is a single positive integer n, telling the number of test scenarios to follow. Each test scenario begins with a line containing a single positive integer p<40000, the number of ports on the two functional blocks. Then follow p lines, describing the signal mapping: On the i:th line is the port number of the block on the right side which should be connected to the i:th port of the block on the left side.
Output
For each test scenario, output one line containing the maximum number of signals which may be routed on the silicon surface without crossing each other.
Sample Input
4642631510234567891018876543219589231746
Sample Output
3914
最长上升子序列(LIS)的典型变形,熟悉的n^2的动归会超时。LIS问题可以优化为nlogn的算法。
定义d[k]:长度为k的上升子序列的最末元素,若有多个长度为k的上升子序列,则记录最小的那个最末元素。
注意d中元素是单调递增的,下面要用到这个性质。
首先len = 1,d[1] =a[1],然后对a[i]:若a[i]>d[len],那么len++,d[len] =a[i];
否则,我们要从d[1]到d[len-1]中找到一个j,满足d[j-1]<a[i]<d[j],则根据D的定义,我们需要更新长度为j的上升子序列的最末元素(使之为最小的)即d[j] = a[i];
最终答案就是len
#include <stdio.h>#include <string.h>#include <algorithm>using namespace std;int a[40005],dp[40005],n;int bin(int size,int k){ int l = 1,r = size; while(l<=r) { int mid = (l+r)/2; if(k>dp[mid]) l = mid+1; else r = mid-1; } return l;}int LIS(){ int i,j,ans=1; dp[1] = a[1]; for(i = 2; i<=n; i++) { if(a[i]<=dp[1]) j = 1; else if(a[i]>dp[ans]) j = ++ans; else j = bin(ans,a[i]); dp[j] = a[i]; } return ans;}int main(){ int t,i; scanf("%d",&t); while(t--) { scanf("%d",&n); for(i = 1;i<=n;i++) scanf("%d",&a[i]); printf("%d\n",LIS()); } return 0;} 0 0
- hdu 1950
- hdu 1950
- HDU 1950
- hdu 1950
- HDU 1950 Bridging signals
- hdu 1950 Bridging signals
- hdu-1950-Bridging signals
- HDU 1950 Bridging signals
- hdu 1950 Bridging signals
- hdu-1950 Bridging signals
- Hdu 1950 bridging signals
- HDU 1950 Bridging signals
- hdu 1950,DP
- HDU:1950 Bridging signals
- hdu 1950 Bridging signals
- HDU 1950 Bridging signals
- HDU 1950 Bridging signals
- hdu 1950 java解法
- javaweb+jasperreports报表+struts2
- android基础笔记:内容提供者及访问(ContentProvider、ContentResolver)
- HDU 4737 A Bit Fun
- RSA算法趣解及C实现(代码,实例,验证过程)
- 不要做一个浮躁的程序员
- hdu 1950
- XCode5显示行号
- hdu1394(线段树点更新的应用)
- UVA 10152 (暑期-线性表-E- ShellSort)
- 让你打开眼界的生活小创意!!!!
- 隐藏的你能发现么
- hdu 1711 Number Sequence
- c# winform实现buttom大小的改变
- enctype="multipart/Form-data"取不到值


