A - Nearest Common Ancestors(8.1.1)
来源:互联网 发布:去哪里下载ubuntu 编辑:程序博客网 时间:2024/06/01 13:08
Description
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:
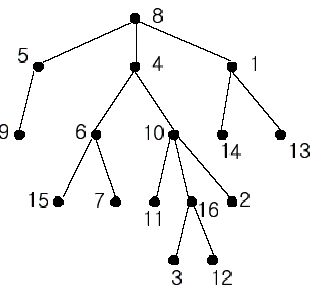
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.

In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2161 148 510 165 94 68 44 101 136 1510 116 710 216 38 116 1216 752 33 43 11 53 5
Sample Output
43
#include <iostream>#include <vector>#include <cstring>using namespace std;const int N = 10005;vector<int> v[N];int f[N], r[N];void dfs( int u, int dep ) //从dep层的u节点出发,通过先根遍历计算每个节点的层次{ r[u] = dep; //节点u为dep层 for( vector<int>::iterator it = v[u].begin(); it != v[u].end(); it++ ) dfs( *it, dep + 1 ); //递归父节点u的每个儿子}int main(){ int cases, i, n, x, y; cin >> cases; while( cases-- ) { cin >> n; v[0].push_back(-1); //为了方便理解,将容器第一个数据节点初始化为-1,此处不用。 for( i = 1; i <= n; i++ ) v[i].clear(); memset( f, 255, sizeof(f) ); for( i = 1; i < n; i++ ) { cin >> x >> y; v[x].push_back(y); //多重链表,将节点y 压入节点x的儿子列表 f[y] = x; //双亲表,将节点y的父节点设为x } for( i = 1; f[i] >= 0; i++ ); //搜索根节点i dfs( i, 1 ); cin >> x >> y; while( x != y ) //若x与y不同,则分析x和y的层次,若x处于较深层次,则取x的父节点为x,否则取y的父节点为y, //直到x = y为止,此时x或者y为最近公共祖先 { if( r[x] > r[y] ) x = f[x]; else y = f[y]; } cout << x << endl; } return 0;} 0 0
- A - Nearest Common Ancestors(8.1.1)
- A - Nearest Common Ancestors(8.1.1)
- (Vedctor经典)A - Nearest Common Ancestors(8.1.1)
- POJ1330(Nearest Common Ancestors)
- poj1330 Nearest Common Ancestors()
- [PKU 1330]Nearest Common Ancestors(LCA)
- poj Nearest Common Ancestors(LCA+Tarjan)
- (简单LCA) Nearest Common Ancestors(P1330)
- Nearest Common Ancestors(最近公共祖先)
- POJ 1330 Nearest Common Ancestors(树)
- poj 1330 Nearest Common Ancestors(LCA)
- POJ 1330 Nearest Common Ancestors (LAC)
- 【POJ 1330】 Nearest Common Ancestors(LCA)
- poj 1330 Nearest Common Ancestors(LCA)
- POJ 1330Nearest Common Ancestors(LCA)
- POJ 1330 Nearest Common Ancestors(Tarjan)
- poj_1330 Nearest Common Ancestors(LCA)
- 【POJ 1330】Nearest Common Ancestors(LCA_trajan)
- 中文字体的英文别名
- 学习笔记:ListView的动态加载。
- MVC页面传值
- TestRunLength
- 函数指针与回调函数
- A - Nearest Common Ancestors(8.1.1)
- 有一种状态,叫 隐身可见!有一种感情,叫 自作多情!
- EBS开发——Form开发积累的常用代码
- CSAPP 书附带的代码中找不到的 config.h 在此给出(坑爹啊。。。)
- Oracle Goldengate添加同步对象到已有的同步队列
- 用JS实现按回车键提交表单----------工作问题005
- java下载 字符串整成的word 文档
- 在iOS中创建静态库
- 操作简便的JPG图片转为PDF转换器


