CodeFroces 445B DZY Loves Chemistry
来源:互联网 发布:python双击闪退 编辑:程序博客网 时间:2024/06/10 06:51
DZY loves chemistry, and he enjoys mixing chemicals.
DZY has n chemicals, and m pairs of them will react. He wants to pour these chemicals into a test tube, and he needs to pour them in one by one, in any order.
Let's consider the danger of a test tube. Danger of an empty test tube is 1. And every time when DZY pours a chemical, if there are already one or more chemicals in the test tube that can react with it, the danger of the test tube will be multiplied by 2. Otherwise the danger remains as it is.
Find the maximum possible danger after pouring all the chemicals one by one in optimal order.
The first line contains two space-separated integers n and m 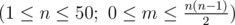 .
.
Each of the next m lines contains two space-separated integers xi and yi (1 ≤ xi < yi ≤ n). These integers mean that the chemical xi will react with the chemical yi. Each pair of chemicals will appear at most once in the input.
Consider all the chemicals numbered from 1 to n in some order.
Print a single integer — the maximum possible danger.
1 012 11 223 21 22 34In the first sample, there's only one way to pour, and the danger won't increase.
In the second sample, no matter we pour the 1st chemical first, or pour the 2nd chemical first, the answer is always 2.
In the third sample, there are four ways to achieve the maximum possible danger: 2-1-3, 2-3-1, 1-2-3 and 3-2-1 (that is the numbers of the chemicals in order of pouring).
题目链接 :http://codeforces.com/problemset/problem/445/B
题目大意 :有n种化学物质和m对反应关系,初始危险系数为1,反应一次危险系数*2,求最大危险系数
题目分析 :两两之间发生反应,则可将有连系的一组放在一个集合中,因此本题是一道并查集问题
#include <cstdio>int const MAX = 55;int father[MAX];void UFset(int n) //初始化并查集{ for(int i = 1; i <= n; i++) father[i] = i;}int Find(int n) //压缩路径{ return n == father[n] ? n : father[n] = Find(father[n]);}void Union(int R1, int R2) //合并{ int r1 = Find(R1); int r2 = Find(R2); father[r1] = r2;}int main(){ int n, m; int x, y; long long ans; //注意数据范围 while(scanf("%d %d",&n, &m) != EOF) { ans = 1; UFset(n); while(m--) { scanf("%d %d",&x, &y); //若x和y不在一个集合中,则合并他们,答案乘2 if(Find(x) != Find(y)) { Union(x,y); ans *= 2; } } printf("%lld\n", ans); }}- CodeFroces 445B DZY Loves Chemistry
- 445B - DZY Loves Chemistry
- Codeforces 445B. DZY Loves Chemistry
- Codeforces 445B DZY Loves Chemistry
- E--DZY Loves Chemistry(CF-445B
- CODEFORCES 445B DZY Loves Chemistry
- Codeforces 445B DZY Loves Chemistry
- CodeForces 445B DZY Loves Chemistry
- codeforces-B. DZY Loves Chemistry
- CodeForces 445B. DZY Loves Chemistry(并查集)
- CF 445B(DZY Loves Chemistry-求连通块)
- Codeforces 445B DZY Loves Chemistry(并查集)
- CodeForces 445B DZY Loves Chemistry(并查集)
- CodeForces 445B DZY Loves Chemistry (并查集)
- CodeForces 445B - DZY Loves Chemistry(并查集)
- 【codeforces 445B - DZY Loves Chemistry 】 + 并查集
- CodeForces 445B DZY Loves Chemistry (并查集)
- codeforces 445 B. DZY Loves Chemistry (并查集)
- poj 3070 Fibonacci (矩阵快速幂求斐波那契数列的第n项)
- Activity 视图相关类 4.4
- UML九类图
- Android调试之tombstone信息的分析
- 双链表&链表合并&多项式相加算法
- CodeFroces 445B DZY Loves Chemistry
- Sort List LeetCode
- iOS音频播放 (一):概述 转
- poj 2540 && uva 10084 Hotter Colder(半平面交)
- 取数游戏_签到积分
- hdu 1010 Tempter of the Bone
- poj 1015 Jury Compromise dp
- 黑马程序员_集合框架工具类
- sizeof小结


