RSA算法学习笔记(未完)

来源：互联网发布：musca linux 编辑：程序博客网时间：2024/06/06 05:01

1 RSA的历史

2 RSA的原理

2.1 欧拉定理

2.2 费马小定理

若p是质数，则对于任意一个整数a，有a^p − a 是p的整数倍，即

a^p \equiv a \pmod p.

若a不能被p整除，则a^p − 1 − 1同样是p的整数倍。

2.3 欧几里得引理

若n是a*b的因子(a*b能被n整除)，且n与a互质，则n是b的因子(b能被n整除)。可以表示为：若n | (a*b)，且gcd(n,a) = 1, 则n | b。

3 RSA应用过程

3.1 密钥生成

RSA算法包括2个密钥：公共密钥(public key)和私有密钥(private key)。一般来讲，如果A和B要实现RSA加密通讯，那么A和B必须将自己的公共密钥告诉对方，当一方需要向另外一方发送加密信息时，则将明文用对方的公共密钥加密为密文，对方在接收到密文后，用自己的私有密钥对密文进行解密得到明文。举个例子：若A向B发送数据，A先用B的公共密钥将明文进行加密得到密文后再将数据发过去，B收到密文后用B的私有密钥进行解密得到了明文。就这么简单。

密钥生成的具体过程如下：

1.随机生成两个不同的质数p和q，由此可知p和q互质。此外，p和q的二进制数的bit位长度要相近；判断两个数是否互质一般使用米勒-拉宾素性检测。

2.计算 n = p * q。

3.计算欧拉函数：φ(n) = φ(p)φ(q) = (p − 1)(q − 1) = n - (p + q -1),φ(n)表示与n为互质的小于等于n的正整数的个数。

4.选取e，满足1 < e < φ(n)且e与φ(n)互质，即gcd(e, φ(n)) = 1。e和n构成公共密钥，e的二进制数bit位长度和汉明重量都不能取得太大（对于二进制数来说，汉明重量指的是1的个数，如11101 0B的汉明重量为4），一般取2^16 + 1 = 65,537，e的值越小安全性越差。

5.选取d满足d ≡ (e^−1) (mod φ(n))，即ed ≡ 1(mod φ(n)), d和n构成私有密钥。

3.2 加密过程

假设整数m为明文，则密文 $c \equiv m^e \pmod{n}$ ，此为模幂运算。

3.3 解密过程

若c是密文，则明文

m \equiv c^d \pmod{n}

，同样是模幂运算。

4 RSA的具体实现过程

其实稍微懂一点数论，上述的应用过程非常容易理解，但是要具体应用在嵌入式编程中，尤其是系统资源不充足时，就是一个比较棘手的问题。尤其在实际应用中，N的二进制位数要达到1024bit才能算是相对安全，那么对于上述的算法来说，基于1024位数的运算绝对是大数运算了，因为目前嵌入式芯片最高也就是32位的。因此，大数运算是难点之一；其次，如何快速实现上述的一些复杂运算，比如求参数d，模幂运算，判断两个大数是否互质等几个问题，因为有现成的一些公式和算法因此相对容易些。

4.1 如何生成随机数？

这个好解决，对于嵌入式系统来说，生成随机数需要一个自然随机的模拟量，比如采集某个置空的AD脚，每次读取时只取bit0的数据(0或1)作为随机数的bit0，每次获取一次随机的0或1都要先将原来的值左移一位，然后将此次的随机值作为bit0，之后，要满足随机数的位数，则可以把最高位置1。

4.2 如何判断一个随机数为质数？

4.2.1 概率性测试

对一个数进行素性检测可以通过多种办法，如费马素性检测、米勒-拉宾素性检测、索尔维-施特拉森素性检测等。这里将详细介绍米勒-拉宾素性检测。

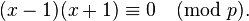首先，在有限域Z/pZ中，如果某个大于2的整数是素数，则对于公式 $x^{2} \equiv 1\pmod{p}$ ，x的解不是1(mod p)就是-1(mode p)。怎么理解？这里我们需要引用欧几里得引理（见上文），公式 $x^{2} \equiv 1\pmod{p}$ 可以转换成 $(x - 1)( x + 1) \equiv 0\pmod{p}.$ 因为p是素数

0 0