支持向量机

转载自：http://www.cnblogs.com/superhuake/archive/2012/07/24/2606298.html

上学的时候，在《模式识别》课程里面接触到支持向量机，但说实话，那时候对它一知半解。虽然当时完成了一个大作业，效果也不错，但终究对它有一种似是而非的感觉。为了不让这种感觉再继续下去，这段时间好好研究一下。接下来会用几篇日志记载这段时间的收获。

    要学习支持向量机，先从我教材《模式识别》（边肇祺，张学工版）出发。这次看书的时候对书上297页的一个地方，也就是最优分类面：

        

 

的分类间隔是 具体怎么推导出来有点不明白，书上的推导过程是放在4.1节即“线性判别函数”那一节。现在来看看具体的推导过程：

    给出两类情况下判别函数为线性的一般表达式：

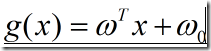            （1）

        式中x是d维特征向量，又称样本向量，w称为权向量， 是阈值权。则可以采用下面的决策规则：

    令

    

如果

       （2）

    方程g(x)实际上定义了一个决策面，将归类为 的点与归类为 的点分割开来。如果g(x)为线性函数，则这个决策面是超平面。假设 和 都是决策面上的点，则有：

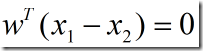             或      （3）

这表明w和超平面上任意向量正交，即w垂直于超平面。

    判别函数g(x)可以看成是特征空间中某点x到超平面的距离的一种代数度量。

    把x表示成：

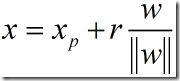           （4）

式中， 是x在H上的投影向量

    r是x到H的垂直距离

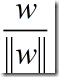         是w方向上的单位向量。

    其实上面的式子就是把一个向量做正交分解，这个我们在高中物理中就学过了，因而这一块是没有问题的。

    将（4）式代入（1）式，可得到：

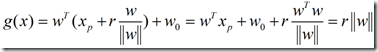           或写作

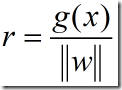               （5）

示意图如下图所示：

        

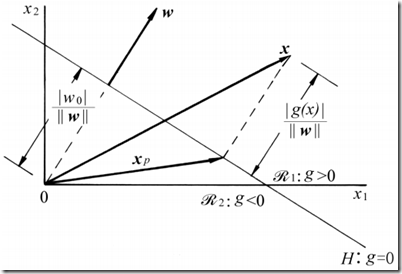
        其实让我有疑问的是公式（5）中的那一长串，原因是我被上面这张图误导了。这张图让我产生了一种错觉，让我以为 是垂直于 向量，那么就应该有。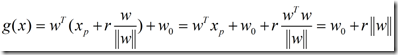

    结果我推来推去老得到超平面经过原点的结论。后来经过仔细阅读书上的文字，突然醒悟。原来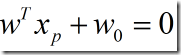 是一个很直观的结论，因为 是x在超平面上的投影，那么就意味着 在超平面上，而超平面上的点必须满足（1）式等于0。 其实，只要将上图中那条斜线看成一个平面，这样的错误就不会产生了，因为这时候能很明显的感觉到 跟超平面是有夹角的。

    一旦把这一关打通，后面就好理解了。

    后记：有时候人一旦陷入一个思维怪圈，就很难走出来。其实看明白之后，会发现自己在纠结一个最简单的问题，但如果没反应过来，那它就越来越复杂。生活中很多事情都是如此。

最近看了张学工老师的《关于统计学习理论与支持向量机》和Vapnik的《Support Vector Networks》两篇文章。张学工老师是国内接触SVM比较早的学者，他的这篇文章算是支持向量机的一个综述；而Vapnik先生是SVM的发明者，SVM大牛中的大牛。他的这篇文章据说是支持向量机的第一篇论文。

    我看文献的习惯是先找一篇国内比较好的综述进行阅读，然后从这篇文章中去找相应的英文文献进行阅读。毕竟现在学术界很多新的理论、技术都来源于西方，因此，要想快速的掌握某个理论及其最新进展，阅读英文文献必不可少；如果想快速形成对所研究事物的初步看法并且想知道应该去找哪些英文文献来阅读的话，阅读国内的综述性文章也很必要。

    支持向量机其实是分类思想发展的必然结果，可以说，从Fisher先生1936年提出Fisher线性判别而导致模式分类技术的诞生开始，就已经注定了终有一天，支持向量机SVM会出现。SVM是一种有监督的机器学习，它的目的是根据训练集给出的样本来求取对系统输入输出关系的估计，当然，这种估计越准确越好。下面就是学习机的一个基本模型。

        

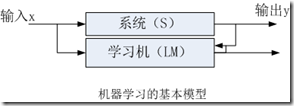
    （1）线性判别函数

    如同上一篇所讲的，对于一个线性可分的两类问题，可以定义一个表达式

             （1）

其中x是d维特征向量，w是权向量， 是阈值权。则可以采用如下的决策规则：

        

分类策略如下：

              （2）

        事实上，g(x)定义了一个决策面，也叫分类面，将 和 中的样本区分开来。通过上一篇中的证明，我们知道g(x)定义的超平面把特征空间分成了两个决策区域，超平面方向由 决定，位置由阈值权 决定，判别函数正比于x到超平面的代数距离，即 。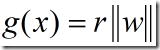

   （2）广义线性判别函数

    线性判别函数虽然简单，但是局限性很大，因为实际问题往往都非常复杂，不可能都是非线性这么简单。因此，对于非线性问题，当然要建立非线性判别函数了。例如对于下面的二阶问题：

        

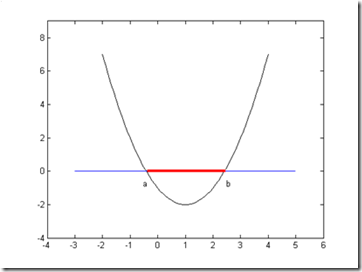
    如上图所示的两类问题，如果x<b或者x>a，则x属于 类；如果b<x<a，则x属于 类。那么定义二次判别函数：

             （3）

就可以很好地解决上面的分类问题，决策规则为：

        

   二次判别函数可以写成：

     （4）

    上面的二次分类器能很好地将数据分开，但我们知道，当判别函数的阶数越高的话，整个系统就越复杂，我们可能根本无法得出这样高阶的模型。但是这里出现了一种新思想，一种对以后分类器设计影响非常大的思想，那就是广义线性判别函数。

    广义线性判别是找到一种适当的 映射，则可以把二次判别函数化为z的线性函数

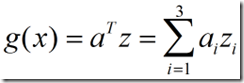      （5）

式中：

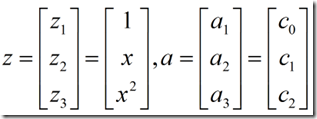
 就是广义线性判别函数，a就是广义权向量。

广义线性判别函数的一般表达式：

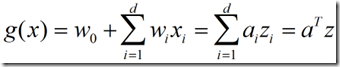     （6）

其中

    

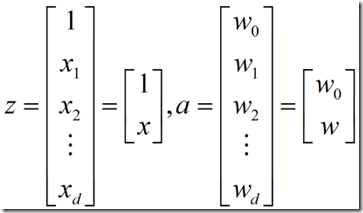
 叫做增广样本向量，a叫做增广权向量，它们是 维向量。因此这是一种将低维上的非线性问题转化到高维上的线性问题的思想。

    （3）最优分类面

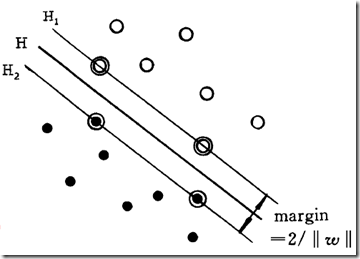
    前面已经说过，线性判别函数或者广义线性判别函数实际上定义了一系列分类面，用来将训练样本无错误地分开。如下图所示：

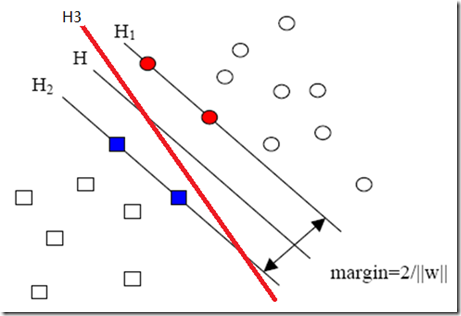
要想将图中的两个类分开，可以有很多分类面H，但是，究竟哪个面最好呢？图中的H3也能将两类分开，难道我们要选它作为分类面吗？

    SVM就是从线性可分情况下的最优分类面（Optimal Hyperplane）提出的。如上图所示，考虑两类线性可分情况，H为把两类没有错误地分开的分类线， , 分别为过各类样本中离分类线最近且平行于分类线的直线， 和 之间的距离叫做两类的分类间隔。

    所谓最优分类面就是要求分类面不但能将两类无错误地分开，而且要使两类的分类间隔最大。很显然，上图中的H3不是一个最优分类面。

    设线性可分样本集为 是类别标号。d维空间中线性判别函数的一般形式是 ，分类面方程为：

                 （7）

将判别函数归一化，则分类间隔变为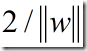 （推导过程见前一节），因此要使间隔最大，则要使 最小或者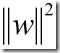 最小。而要求对所有样本正确分类，则要满足：

    （8）

满足上面条件且使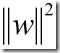最小的分类面就是最优分类面。过两类样本中离分类面最近的点且平行于最优分类面的超平面 和 上的训练样本就是使（8）中等号成立的样本，叫做支持向量。所以对于支持向量这个名字我们要注意，它指的还是训练集中的样本，只不过是特殊的样本。

    最优分类面问题可以转化成下面的约束优化问题，即在（8）的约束下求函数

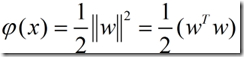             （9）的最小值，为此，可以构造如下的Lagrange函数：

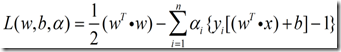            (10)

其中 为Lagrange系数，对w和b求Lagrange函数的最小值。

    通过求偏导和对偶原理，上面的问题转化为在约束

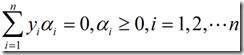              （11）                 这个式子是可以通过对b求偏导得到

之下对 求解下列函数的最大值：

            （12）

若 为最优解，则

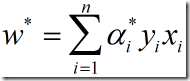             （13）

从（13）中可以看出，最优分类面的权系数向量是训练集样本向量的线性组合。当然，一旦权向量出来了，b就很好求了，只要将支持向量代入表达式（8）使等号成立即可。这是一个约束条件下的二次寻优问题，存在唯一解。根据Kuhn-Tucker条件，这个优化问题必须满足

        

最终得到的最优分类函数可以用一个符号函数来表示：

              （14）

    后记：这里只是简单讨论最简单的支持向量机的诞生过程，支持向量机是统计学习理论发展的集大成，具有很多新的特点，接下来将着重讲述在简单线性可分支持向量机基础上的扩展。

第二篇主要是讲述了SVM中最简单的情况，也就是线性可分的两类问题。在前面给出的公式中，对Lagrange函数的产生过程及接下来的推导还是有一些疑问，后来查了一些资料，终于释放掉心中的疑云，现记录如下。

    有疑问的地方是：

    前文说的最优分类面问题转化成如下的约束优化问题，即在条件

         的约束下，求函数

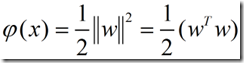     的最小值。这是没问题的，但是紧接着作者通过定义一个Lagrange函数将整个问题转化成了另一个极值问题。那么我们先来看看何为Lagrange乘子法。

    Lagrange乘子法：

    其实在上学的时候肯定学过Lagrange乘子法，但说实话现在的印象已经很朦胧了。通过查阅wiki和《模式识别》，加深了对它的了解。

    Lagrange乘子法是一种在等式约束条件下的优化算法。它将一个有n个变量与k个约束条件的最优化问题转化为一个有n+k个变量的方程组的极值问题，其变量不受任何约束。同时它引入了一个标量未知数--Lagrange乘子 。

    一个简单的例子就是：

    最大化 

    受限于 

    引入新变量拉格朗日乘数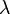，即可求解下列拉格朗日方程

         接下来主要就是通过使偏导的值为0来求出参数。

仿照上面的式子，我们就可以写出自己的Lagrange函数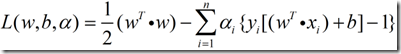：             （1）

接下来进行推导1。

    将（1）式对w和b求偏导，

                 （2）

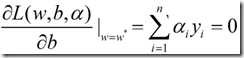                 （3）

由（2），（3）可得

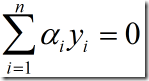               其中     （4）

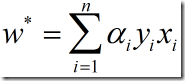              （5）

    将（5）和（4）代入（1），有：

        

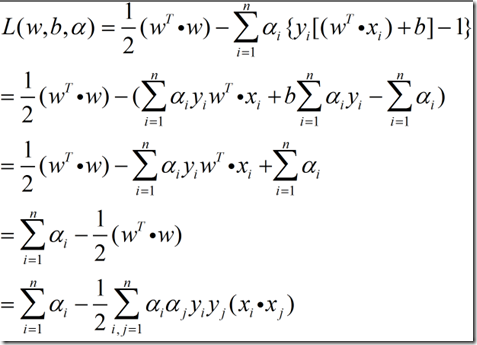
    这样，运算过程基本上就清晰了。