数组、链表、堆栈和队列 (转)
来源:互联网 发布:大话骰软件 编辑:程序博客网 时间:2024/05/05 04:41
数组是随机存储的内存连续的
栈是先进后出内存连续的
队列是先进后先出内存连续的
链表是顺序存储的内存可以不连续
数据结构:是指相互之间存在一种或多种特定关系的数据元素的集合。听起来是不是很抽象,简单理解:数据结构就是描述对象间逻辑关系的学科。比如:队列就是一种先进先出的逻辑结构,栈是一种先进后出的逻辑结构,家谱是一种树形的逻辑结构!(初学数据结构的时候很不理解为什么有“栈”这个东西;队列很容易理解---无论购物就餐都需要排队;栈可以认为就是个栈道---只允许一个人通过的小道,而且只能从一端进入,然后再从这端返回,比如你推了个箱子进去啦,第二个人也推个箱子进去,此时只能等后进来的这个人拉着箱子出去后,你才能退出。)
数据存储结构:它是计算机的一个概念,简单讲,就是描述数据在计算机中存储方式的学科;常用的数据存储方式就两种:顺序存储,非顺序存储!顺序存储就是把数据存储在一块连续的存储介质(比如硬盘或内存)上----举个例子:从内存中拿出第100个字节到1000个字节间的连续位置,存储数据;数组就是典型的顺序存储!非顺序存储就是各个数据不一定存在一个连续的位置上,只要每个数据知道它前面的数据和后面的数据,就能把所有数据连续起来啦;链表就是典型的非顺序存储啦!
数组、链表、堆栈和队列是最基本的数据结构,任何程序都会涉及到其中的一种或多种。
链表的使用不需要知道数据的大小,而数组在创建时必须指明数组的大小。
1数组
数组是最最基本的数据结构,很多语言都内置支持数组。数组是使用一块连续的内存空间保存数据,保存的数据的个数在分配内存的时候就是确定的:

图 1.1包含n个数据的数组
访问数组中第n个数据的时间花费是O(1)但是要在数组中查找一个指定的数据则是O(N)。当向数组中插入或者删除数据的时候,最好的情况是在数组的末尾进行操作,时间复杂度是O(1),但是最坏情况是插入或者删除第一个数据,时间复杂度是O(N)。在数组的任意位置插入或者删除数据的时候,后面的数据全部需要移动,移动的数据还是和数据个数有关所以总体的时间复杂度仍然是O(N)。

图 1.2向数组中插入数据
2链表
链表是在非连续的内存单元中保存数据,并且通过指针将各个内存单元链接在一起,最有一个节点的指针指向NULL。链表不需要提前分配固定大小存储空间,当需要存储数据的时候分配一块内存并将这块内存插入链表中。
在链表中查找第n个数据以及查找指定的数据的时间复杂度是O(N),但是插入和删除数据的时间复杂度是O(1),因为只需要调整指针就可以:

图 2.1链表
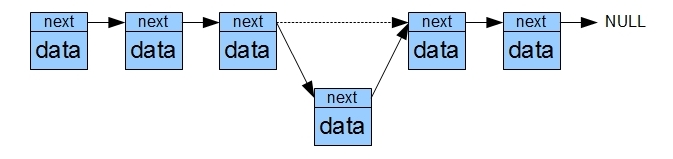
图 2.2向链表中插入一个数据

图 2.3从链表中删除一个数据
向上面这样的链表结构在插入和删除的时候编程会比较困难,因为需要记住当前节点的前一个节点,这样才能完成插入和删除。为了简便通常使用带有头节点的链表:
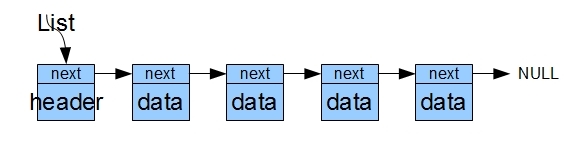
图 2.4带有头节点的单链表
上面的链表是单链表,此外还有双链表,就是节点中包含指向下一个节点的指针和指向上一个节点的指针:
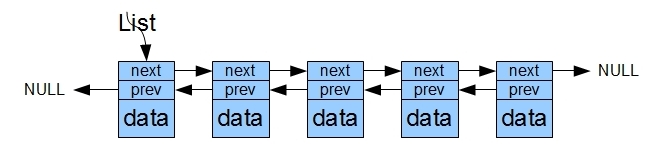
图2.5双向链表
不带有头节点的双向链表在插入和删除数据的时候也不会出现单链表那样的问题。此外还有一种链表是循环链表,它是将双向链表的头尾相接:
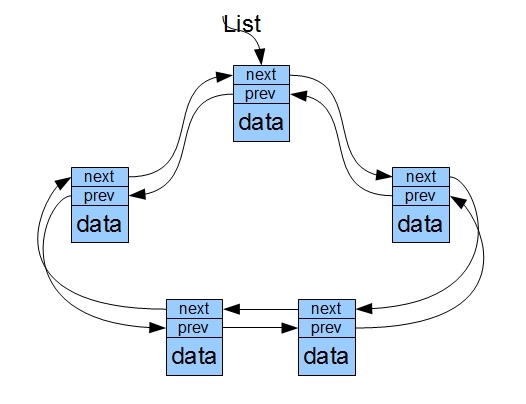
图 2.6双向循环链表
向循环双向链表和循环链表中插入或者从中删除数据只是多移动几个指针。
一个简单结点的结构体表示为:
struct note
{
int data; /*数据成员可以是多个不同类型的数据*/
struct note *next; /*指针变量成员只能是-个*/
};
一个简单的单向链表的图示
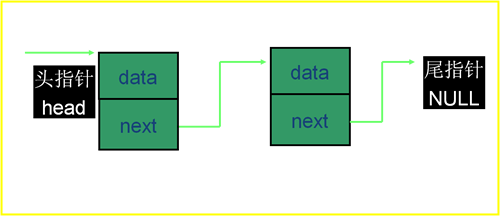
1.链表是结构、指针相结合的-种应用,它是由头、中间、尾多个链环组成的单方向可伸缩的链表,链表上的链环我们称之为结点。
2.每个结点的数据可用-个结构体表示,该结构体由两部分成员组成:数据成员与结构指针变量成员。
3.数据成员存放用户所需数据,而结构指针变量成员则用来连接(指向)下-个结点,由于每-个结构指针变量成员都指向相同的结构体,所以该指针变量称为结构指针变量。
4.链表的长度是动态的,当需要建立-个结点,就向系统申请动态分配-个存储空间,如此不断地有新结点产生,直到结构指针变量指向为空(NULL)。申请动态分配-个存储空间的表示形式为:
(struct note*)malloc(sizeof(struct note))
链表的建立
在链表建立过程中,首先要建立第一个结点,然后不断地
在其尾部增加新结点,直到不需再有新结点,即尾指针指向
NULL为止。
设有结构指针变量 struct note *p,*p1,*head;
head:用来标志链表头;
p:在链表建立过程中,p总是不断先接受系统动态分配的新结点地址。
p1->next:存储新结点的地址。
链表建立的步骤:
第一步:建立第一个结点
struct node
{
int data;
struct node *next;
};
struct note *p,*p1,*head;
head=p1=p=(struct node *)malloc(sizeof(struct node);

第二步:
给第-个结点成员data赋值并产生第二个结点
scanf(“%d”,&p->data); /*输入10*/
p=(struct node *)malloc(sizeof(struct node);

第三步:将第-个结点与第二个结点连接起来
p1-> next=p;
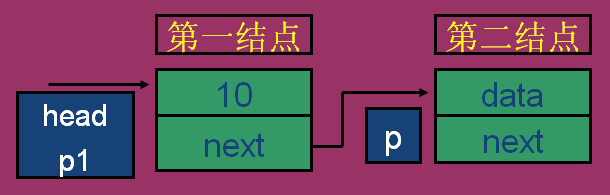
第四步:产生第三个结点
p1=p;
scanf(“%d”,&p->data);/*输入8*/
p=(struct node *)malloc(sizeof(struct node);
以后步骤都是重复第三、四步,直到给出-个结束条件,不再建新的结点时,要有
p->next=NULL;它表示尾结点。
代码
- #include <stdio.h>
- #include<stdlib.h>
- #define LEN sizeof(struct node)
- struct node
- {
- int data;
- struct node *next;
- };
- main()
- { struct node *p, *pl,* head;
- head=p=(struct node * )malloc(LEN);
- scanf("%d",&p->data);/*头结点的数据成员*/
- while(p->data!=0) /*给出0结束条件,退出循环*/
- { pl=p;
- p=(struct node * )malloc(LEN);
- scanf("%d",&p->data);/*中间结点数据成员*/
- pl->next=p;/*中间结点的指针成员值*/
- }
- p-> next=NULL;/*尾结点的指针成员值*/
- p=head;/*链表显示*/
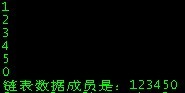
- printf("链表数据成员是:");
- while(p->next!=NULL)
- {
- printf("%d",p->data);
- p=p->next;
- }
- printf("%d\n",p->data);
- }
3堆栈
堆栈实现了一种后进先出的语义(LIFO)。可以使用数组或者是链表来实现它:

图 3.1堆栈
对于堆栈中的数据的所有操作都是在栈的顶部完成的,只可以查看栈顶部的数据,只能够向栈的顶部压入数据,也只能从栈的顶部弹出数据。
4队列
队列实现了先入先出的语义(FIFO)。队列也可以使用数组和链表来实现:

图 4.1队列
队列只允许在队尾添加数据,在队头删除数据。但是可以查看队头和队尾的数据。还有一种是双端队列,在两端都可以插入和删除:
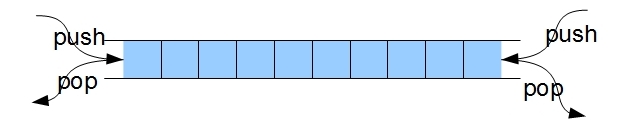
图 4.2双端队列
1.栈
1.1 栈的定义
栈是一种特殊的线性表。其特殊性在于限定插入和删除数据元素的操作只能在线性表的一端进行。如下所示:
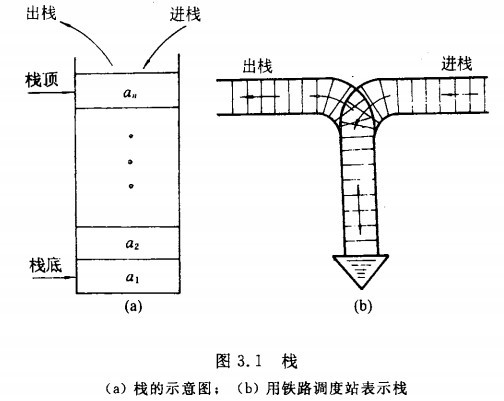
结论:后进先出(Last In First Out),简称为LIFO线性表。
栈的基本运算有六种:
构造空栈:InitStack(S)、
判栈空: StackEmpty(S)、
判栈满: StackFull(S)、
进栈: Push(S,x)、可形象地理解为压入,这时栈中会多一个元素
退栈: Pop(S) 、 可形象地理解为弹出,弹出后栈中就无此元素了。
取栈顶元素:StackTop(S),不同与弹出,只是使用栈顶元素的值,该元素仍在栈顶不会改变。
由于栈也是线性表,因此线性表的存储结构对栈也适用,通常栈有顺序栈和链栈两种存储结构,这两种存储结构的不同,则使得实现栈的基本运算的算法也有所不同。
我们要了解的是,在顺序栈中有"上溢"和"下溢"的概念。顺序栈好比一个盒子,我们在里头放了一叠书,当我们要用书的话只能从第一本开始拿(你会把盒子翻过来吗?真聪明^^),那么当我们把书本放到这个栈中超过盒子的顶部时就放不下了(叠上去的不算,哼哼),这时就是"上溢","上溢"也就是栈顶指针指出栈的外面,显然是出错了。反之,当栈中已没有书时,我们再去拿,看看没书,把盒子拎起来看看盒底,还是没有,这就是"下溢"。"下溢"本身可以表示栈为空栈,因此可以用它来作为控制转移的条件。
链栈则没有上溢的限制,它就象是一条一头固定的链子,可以在活动的一头自由地增加链环(结点)而不会溢出,链栈不需要在头部附加头结点,因为栈都是在头部进行操作的,如果加了头结点,等于要在头结点之后的结点进行操作,反而使算法更复杂,所以只要有链表的头指针就可以了。
1.2 栈的顺序存储
使用c++的面向对象封装:
- // Test.cpp : Defines the entry point for the console application.
- //
- #include "stdafx.h"
- #include <iostream>
- using namespace std;
- #define MAX 10 // MAXIMUM STACK CONTENT
- class stack
- {
- private:
- int arr[MAX];
- int top;
- public:
- stack()
- {
- inItStack();
- }
- /************************************************************************/
- /* 初始化栈 */
- /************************************************************************/
- void inItStack()
- {
- top=-1;
- }
- /************************************************************************/
- /* 入栈 */
- /************************************************************************/
- void push(int a)
- {
- top++;
- if(top < MAX) {
- arr[top]=a;
- } else {
- cout<<"STACK FULL!!"<<top;
- }
- }
- /************************************************************************/
- /* 出栈 */
- /************************************************************************/
- int pop()
- {
- if(isEmpty()) {
- cout<<"STACK IS EMPTY ";
- return NULL;
- } else {
- int data=arr[top];
- arr[top]=NULL;
- top--;
- return data;
- }
- }
- /************************************************************************/
- /* 是否为空 */
- /************************************************************************/
- bool isEmpty()
- {
- if(top == -1) return true;
- else return false;
- }
- };
- int main()
- {
- stack a;
- a.push(3);
- a.push(10);
- a.push(1);
- cout<<"Pop:"<<a.pop();
- return 0;
- }
1.3 栈的链式存储
若是栈中元素的数目变化范围较大或不清楚栈元素的数目,就应该考虑使用链式存储结构。人们将用链式存储结构表示的栈称作"链栈"。链栈通常用一个无头结点的单链表表示。如图所示:
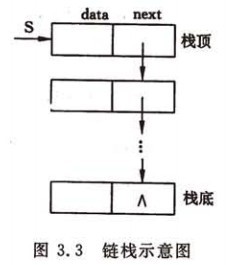
栈的操作是线性表操作的特例。
简单用c实现:
- // Test.cpp : Defines the entry point for the console application.
- //
- #include "stdafx.h"
- #include <stdio.h>
- #include "stdlib.h"
- #include <iostream>
- using namespace std;
- //宏定义
- #define TRUE 1
- #define FALSE 0
- #define OK 1
- #define ERROR 0
- #define INFEASIBLE -1
- #define OVERFLOW -2
- #define STACKEMPTY -3
- #define LT(a,b) ((a)<(b))
- #define N = 100
- typedef int Status;
- typedef int ElemType;
- typedef struct LNode{
- ElemType data;
- struct LNode *next;
- }LNode, *LinkList;
- typedef struct stack{
- LinkList top;
- } STACK;
- /************************************************************************/
- /* 接口:
- */
- /************************************************************************/
- void InitStack(STACK &S);
- void Push(STACK &S,ElemType e);
- void Pop(STACK &S, ElemType *e);
- ElemType GetTop(STACK S,ElemType *e);
- int StackEmpty(STACK S);
- /************************************************************************/
- /*
- */
- /************************************************************************/
- void InitStack(STACK &S)
- {
- S.top=NULL;
- }
- /************************************************************************/
- /* 入栈
- */
- /************************************************************************/
- void Push(STACK &S,ElemType e)
- {
- LinkList p;
- p = (LinkList )malloc(sizeof(LNode));
- if (!p) exit(OVERFLOW);
- p->data = e;
- p->next = S.top;
- S.top = p;
- }
- /************************************************************************/
- /* 出栈
- */
- /************************************************************************/
- void Pop(STACK &S, ElemType *e)
- {
- LinkList p;
- if(StackEmpty(S)) exit(STACKEMPTY);
- *e = S.top->data;
- p = S.top;
- S.top = p->next;
- free(p);
- }
- /************************************************************************/
- /* 获取栈顶元素内容
- */
- /************************************************************************/
- ElemType GetTop(STACK S, ElemType *e)
- {
- if(StackEmpty(S)) exit(STACKEMPTY);
- *e = S.top->data;
- }
- /************************************************************************/
- /* 判断栈S是否空
- */
- /************************************************************************/
- int StackEmpty(STACK S)
- {
- if(S.top==NULL) return TRUE;
- return FALSE;
- }
- void main()
- {
- STACK S;
- InitStack( S);
- Push(S, 3);
- Push(S, 4);
- ElemType e;
- Pop(S,&e);
- cout<<"Pop elem:"<<e;
- }
1.4 栈的应用
1) 数制转换
2)语法词法分析
3)表达式求值等
1.5 栈的递归和实现
汉诺塔的问题:

解决:
1)如果有一个盘子,直接从X移到Z即可。
2)如果有n个盘子要从X移到Z,Y作为辅助。问题可以转化为,先将上面n-1个从X移动到Y,Z作为辅助,然后将第n个从X移动到Z,最后将剩余的n-1个从Y移动到Z,X作为辅助。
完整实现代码,包括栈的实现:
- // Test.cpp : Defines the entry point for the console application.
- //
- #include "stdafx.h"
- #include <stdio.h>
- #include "stdlib.h"
- #include <iostream>
- using namespace std;
- //宏定义
- #define TRUE 1
- #define FALSE 0
- #define OK 1
- #define ERROR 0
- #define INFEASIBLE -1
- #define OVERFLOW -2
- #define STACKEMPTY -3
- #define LT(a,b) ((a)<(b))
- #define N = 100
- typedef int Status;
- typedef int ElemType;
- typedef struct LNode{
- ElemType data;
- struct LNode *next;
- }LNode, *LinkList;
- typedef struct stack{
- LinkList top;
- } STACK;
- /************************************************************************/
- /* 接口:
- */
- /************************************************************************/
- void InitStack(STACK &S);
- void Push(STACK &S,ElemType e);
- void Pop(STACK &S, ElemType *e);
- ElemType GetTop(STACK S,ElemType *e);
- int StackEmpty(STACK S);
- /************************************************************************/
- /*
- */
- /************************************************************************/
- void InitStack(STACK &S)
- {
- S.top=NULL;
- }
- /************************************************************************/
- /* 入栈
- */
- /************************************************************************/
- void Push(STACK &S,ElemType e)
- {
- LinkList p;
- p = (LinkList )malloc(sizeof(LNode));
- if (!p) exit(OVERFLOW);
- p->data = e;
- p->next = S.top;
- S.top = p;
- }
- /************************************************************************/
- /* 出栈
- */
- /************************************************************************/
- void Pop(STACK &S, ElemType *e)
- {
- LinkList p;
- if(StackEmpty(S)) exit(STACKEMPTY);
- *e = S.top->data;
- p = S.top;
- S.top = p->next;
- free(p);
- }
- /************************************************************************/
- /* 获取栈顶元素内容
- */
- /************************************************************************/
- ElemType GetTop(STACK S, ElemType *e)
- {
- if(StackEmpty(S)) exit(STACKEMPTY);
- *e = S.top->data;
- }
- void printStack(STACK S){
- LinkList p;
- p = S.top;
- printf("栈: ");
- while (p) {
- printf("%d ", p->data);
- p = p->next;
- }
- }
- /************************************************************************/
- /* 如果有一个盘子,直接从X移到Z即可。
- 如果有n个盘子要从X移到Z,Y作为辅助。问题可以转化为,先将上面n-1个从X移动到Y,Z作为辅助,然后将第n个从X移动到Z,最后将剩余的n-1个从Y移动到Z,X作为辅助。
- */
- /************************************************************************/
- void move(STACK &Sa,STACK &Sb)
- {
- ElemType e;
- Pop(Sa,&e);
- Push(Sb, e);
- }
- void hanoi(int n,STACK &X,STACK &Y,STACK &Z)
- {
- if(n==1) return move(X, Z); //将圆盘1号直接移到z
- hanoi(n-1,X,Z,Y); //将x上的1大n-1圆盘移到y,z做辅助塔
- move(X, Z); //将编号为n的圆盘移z
- hanoi(n-1,Y,X,Z); //将y上的1大n-1圆盘移到z,x做辅助塔
- }
- /************************************************************************/
- /* 判断栈S是否空
- */
- /************************************************************************/
- int StackEmpty(STACK S)
- {
- if(S.top==NULL) return TRUE;
- return FALSE;
- }
- void main()
- {
- STACK Sx, Sy,Sz;
- InitStack( Sx);
- InitStack( Sy);
- InitStack( Sz);
- int i, n = 10;
- for (i = 10 ; i>=1 ;i--) {
- Push(Sx, i);
- }
- printStack(Sx);
- hanoi(n, Sx,Sy,Sz);
- printStack(Sz);
- }
1.队列
1.1 队列定义
队列(Queue)也是一种运算受限的线性表,它的运算限制与栈不同,是两头都有限制,插入只能在表的一端进行(只进不出),而删除只能在表的另一端进行(只出不进),允许删除的一端称为队尾(rear),允许插入的一端称为队头 (Front)
,队列的操作原则是先进先出的,所以队列又称作FIFO表(First In First Out)
队列的基本运算也有六种:
置空队 :InitQueue(Q)
判队空: QueueEmpty(Q)
判队满: QueueFull(Q)
入队 : EnQueue(Q,x)
出队 : DeQueue(Q)
取队头元素: QueueFront(Q),不同与出队,队头元素仍然保留。
队列也有顺序存储和链式存储两种存储结构,前者称顺序队列,后者为链队。
对于顺序队列,我们要理解"假上溢"的现象。
我们现实中的队列比如人群排队买票,队伍中的人是可以一边进去从另一头出来的,除非地方不够,总不会有"溢出"的现象,相似地,当队列中元素完全充满这个向量空间时,再入队自然就会上溢,如果队列中已没有元素,那么再要出队也会下溢。
那么"假上溢"就是怎么回事呢?
因为在这里,我们的队列是存储在一个向量空间里,在这一段连续的存储空间中,由一个队列头指针和一个尾指针表示这个队列,当头指针和尾指针指向同一个位置时,队列为空,也就是说,队列是由两个指针中间的元素构成的。在队列中,入队和出队并不是象现实中,元素一个个地向前移动,走完了就没有了,而是指针在移动,当出队操作时,头指针向前(即向量空间的尾部)增加一个位置,入队时,尾指针向前增加一个位置,在某种情况下,比如说进一个出一个,两个指针就不停地向前移动,直到队列所在向量空间的尾部,这时再入队的话,尾指针就要跑到向量空间外面去了,仅管这时整个向量空间是空的,队列也是空的,却产生了"上溢"现象,这就是假上溢。
为了克服这种现象造成的空间浪费,我们引入循环向量的概念,就好比是把向量空间弯起来,形成一个头尾相接的环形,这样,当存于其中的队列头尾指针移到向量空间的上界(尾部)时,再加1的操作(入队或出队)就使指针指向向量的下界,也就是从头开始。这时的队列就称循环队列。
通常我们应用的大都是循环队列。由于循环的原因,光看头尾指针重叠在一起我们并不能判断队列是空的还是满的,这时就需要处理一些边界条件,以区别队列是空还是满。方法至少有三种,一种是另设一个布尔变量来判断(就是请别人看着,是空还是满由他说了算),第二种是少用一个元素空间,当入队时,先测试入队后尾指针是不是会等于头指针,如果相等就算队已满,不许入队。第三种就是用一个计数器记录队列中的元素的总数,这样就可以随时知道队列的长度了,只要队列中的元素个数等于向量空间的长度,就是队满。
2.2 队列的顺序存储
顺序存储如图:
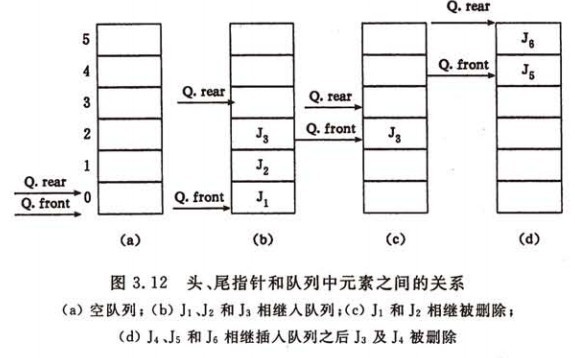
由于是顺序存储结构的存储空间是静态分配的,所以在添加数据的时,有可能没有剩余空间的情况。
解决这种“假溢出”情况,使用循环队列。在c语言中,不能用动态分配的一维数组来实现循环队列。若使用循环队列,必须设置最大队列长度,若无法估计最大长度,就使用链式队列。
c实现:
- // Test.cpp : Defines the entry point for the console application.
- //
- #include "stdafx.h"
- #include <stdio.h>
- #include "stdlib.h"
- #include <iostream>
- using namespace std;
- //宏定义
- #define TRUE 1
- #define FALSE 0
- #define OK 1
- #define ERROR 0
- #define INFEASIBLE -1
- #define OVERFLOW -2
- #define QUEUEEMPTY -3
- #define MAX_QUEUE 10 //队列的最大数据元素数目
- typedef int Status;
- typedef int ElemType;
- typedef struct queue{
- ElemType elem[MAX_QUEUE] ; ///假设当数组只剩下一个单元时认为队满
- int front; //队头指针
- int rear; //队尾指针
- }QUEUE;
- /************************************************************************/
- /* 各项基本操作算法。
- */
- /************************************************************************/
- void InitQueue(QUEUE *&Q);
- void EnQueue(QUEUE *Q,ElemType elem);
- void DeQueue(QUEUE *Q,ElemType *elem);
- int QueueEmpty(QUEUE Q);
- /************************************************************************/
- /*
- 初始化
- 直接使用结构体指针变量,必须先分配内存地址,即地址的指针
- */
- /************************************************************************/
- void InitQueue(QUEUE *&Q)
- {
- Q = (QUEUE *) malloc (sizeof(QUEUE));
- Q->front = Q->rear = -1;
- }
- /************************************************************************/
- /* 入队
- */
- /************************************************************************/
- void EnQueue(QUEUE *Q, ElemType elem)
- {
- if((Q->rear+1)% MAX_QUEUE == Q->front) exit(OVERFLOW);
- Q->rear = (Q->rear + 1)%MAX_QUEUE;
- Q->elem[Q->rear] = elem;
- }
- /************************************************************************/
- /* 出队
- */
- /************************************************************************/
- void DeQueue(QUEUE *Q,ElemType *elem)
- {
- if (QueueEmpty(*Q)) exit(QUEUEEMPTY);
- Q->front = (Q->front+1) % MAX_QUEUE;
- *elem=Q->elem[Q->front];
- }
- /************************************************************************/
- /* 获取队头元素内容
- */
- /************************************************************************/
- void GetFront(QUEUE Q,ElemType *elem)
- {
- if ( QueueEmpty(Q) ) exit(QUEUEEMPTY);
- *elem = Q.elem[ (Q.front+1) % MAX_QUEUE ];
- }
- /************************************************************************/
- /* 判断队列Q是否为空
- */
- /************************************************************************/
- int QueueEmpty(QUEUE Q)
- {
- if(Q.front==Q.rear) return TRUE;
- else return FALSE;
- }
- void main()
- {
- QUEUE *Q;
- InitQueue( Q);
- EnQueue( Q, 1);
- EnQueue( Q, 2);
- ElemType e;
- DeQueue( Q,&e);
- cout<<"De queue:"<<e;
- }
注意:InitQueue(QUEUE *&Q) 传的是指针的地址。
2.3 链式队列:
- // Test.cpp : Defines the entry point for the console application.
- //
- #include "stdafx.h"
- #include <stdio.h>
- #include "stdlib.h"
- #include <iostream>
- using namespace std;
- //宏定义
- #define TRUE 1
- #define FALSE 0
- #define OK 1
- #define ERROR 0
- #define INFEASIBLE -1
- #define OVERFLOW -2
- #define QUEUEEMPTY -3
- typedef int Status;
- typedef int ElemType;
- typedef struct LNode { //链式队列的结点结构
- ElemType elem; //队列的数据元素类型
- struct LNode *next; //指向后继结点的指针
- }LNode, *LinkList;
- typedef struct queue{ //链式队列
- LinkList front; //队头指针
- LinkList rear; //队尾指针
- }QUEUE;
- /************************************************************************/
- /* 各项基本操作算法。
- */
- /************************************************************************/
- void InitQueue(QUEUE *Q);
- void EnQueue(QUEUE *Q,ElemType elem);
- void DeQueue(QUEUE *Q,ElemType *elem);
- void GetFront(QUEUE Q,ElemType *elem) ;
- bool QueueEmpty(QUEUE Q);
- /************************************************************************/
- /*初始化队列Q */
- void InitQueue(QUEUE *Q)
- {
- Q->front = (LinkList)malloc(sizeof(LNode));
- if (Q->front==NULL) exit(ERROR);
- Q->rear= Q->front;
- }
- /*入队 */
- void EnQueue(QUEUE *Q,ElemType elem)
- {
- LinkList s;
- s = (LinkList)malloc(sizeof(LNode));
- if(!s) exit(ERROR);
- s->elem = elem;
- s->next = NULL;
- Q->rear->next = s;
- Q->rear = s;
- }
- /*出队 */
- void DeQueue(QUEUE *Q,ElemType *elem)
- {
- LinkList s;
- if(QueueEmpty(*Q)) exit(ERROR);
- *elem = Q->front->next->elem;
- s = Q->front->next;
- Q->front->next = s->next;
- free(s);
- }
- /*获取队头元素内容 */
- void GetFront(QUEUE Q,ElemType *elem)
- {
- if(QueueEmpty(Q)) exit(ERROR);
- *elem = Q.front->next->elem;
- }
- /*判断队列Q是否为空 */
- bool QueueEmpty(QUEUE Q)
- {
- if(Q.front == Q.rear) return TRUE;
- return FALSE;
- }
- void main()
- {
- QUEUE Q;
- InitQueue( &Q);
- EnQueue( &Q, 1);
- EnQueue( &Q, 2);
- ElemType e;
- DeQueue( &Q,&e);
- cout<<"De queue:"<<e;
- }
【举例1】银行排队
【举例2】模拟打印机缓冲区。
在主机将数据输出到打印机时,会出现主机速度与打印机的打印速度不匹配的问题。这时主机就要停下来等待打印机。显然,这样会降低主机的使用效率。为此人们设想了一种办法:为打印机设置一个打印数据缓冲区,当主机需要打印数据时,先将数据依次写入这个缓冲区,写满后主机转去做其他的事情,而打印机就从缓冲区中按照先进先出的原则依次读取数据并打印,这样做即保证了打印数据的正确性,又提高了主机的使用效率。由此可见,打印机缓冲区实际上就是一个队列结构。
【举例3】CPU分时系统
在一个带有多个终端的计算机系统中,同时有多个用户需要使用CPU运行各自的应用程序,它们分别通过各自的终端向操作系统提出使用CPU的请求,操作系统通常按照每个请求在时间上的先后顺序,将它们排成一个队列,每次把CPU分配给当前队首的请求用户,即将该用户的应用程序投入运行,当该程序运行完毕或用完规定的时间片后,操作系统再将CPU分配给新的队首请求用户,这样即可以满足每个用户的请求,又可以使CPU正常工作。
- 数组、链表、堆栈和队列 (转)
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈和队列
- 数组、链表、堆栈、队列和树
- 链表、数组和堆栈、队列详解
- 数组、链表、堆栈和队列学习
- Unity3D学习之(习题练习)
- HEVC代码追踪(三):encode->compressGOP
- 继承注意的问题
- 第十三周 项目2 输入班级的人数及成绩三种方法(续3)
- MDK-Debug设置之Download to Flash
- 数组、链表、堆栈和队列 (转)
- 技术男与业务男的对话
- log4net配置使用说明
- typedef与define
- winform中axframerControl控件出现System.Reflection.TargetInvocationException
- SunDayApp天气源码
- mysql error table
- MD5
- Manpage: start-stop-daemon


