数据挖掘基础知识-矩阵(分解)
来源:互联网 发布:versions for mac过期 编辑:程序博客网 时间:2024/06/05 03:25
1. 矩阵知识:
//特征值,行列式,秩,对称矩阵,单位矩阵,正定半正定,雅可比等等!!
正交矩阵:
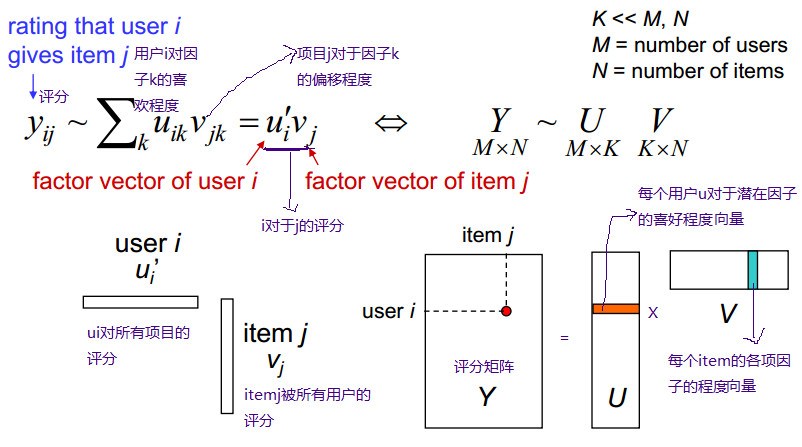
用用户对电影来举例子就是:每个用户看电影的时候都有偏好,这些偏好可以直观理解成:恐怖,喜剧,动作,爱情等。用户——特性矩阵表示的就是用户对这些因素的喜欢程度。同样,每一部电影也可以用这些因素描述,因此特性——物品矩阵表示的就是每一部电影这些因素的含量,也就是电影的类型。这样子两个矩阵相乘就会得到用户对这个电影的喜欢程度。
SVD分解:
matlab code:
>> A
A =
1 2 3 4 5
4 3 2 1 4
>> [u,s,v] = svd(A);
>> u
u =
-0.7456 -0.6664
-0.6664 0.7456
>> s
s =
9.5264 0 0 0 0
0 3.2012 0 0 0
>> v
v =
-0.3581 0.7235 -0.2591 -0.1658 -0.5038
-0.3664 0.2824 0.2663 0.8031 0.2647
-0.3747 -0.1587 0.8170 -0.2919 -0.2858
-0.3830 -0.5998 -0.3560 0.3230 -0.5123
-0.6711 -0.1092 -0.2602 -0.3714 0.5762
SVD与推荐系统:(http://blog.csdn.net/wuyanyi/article/details/7964883)
-------------------------------------------------------------------------------------
直观地说:
假设我们有一个矩阵,该矩阵每一列代表一个user,每一行代表一个item。

如上图,ben,tom....代表user,season n代表item。
矩阵值代表评分(0代表未评分):
如 ben对season1评分为5,tom对season1 评分为5,tom对season2未评分。
机器学习和信息检索:
机器学习的一个最根本也是最有趣的特性是数据压缩概念的相关性。
如果我们能够从数据中抽取某些有意义的感念,则我们能用更少的比特位来表述这个数据。
从信息论的角度则是数据之间存在相关性,则有可压缩性。
SVD就是用来将一个大的矩阵以降低维数的方式进行有损地压缩。
降维:
下面我们将用一个具体的例子展示svd的具体过程。
首先是A矩阵。
A =
5 5 0 5
5 0 3 4
3 4 0 3
0 0 5 3
5 4 4 5
5 4 5 5
(代表上图的评分矩阵)
使用matlab调用svd函数:
[U,S,Vtranspose]=svd(A)
U =
-0.4472 -0.5373 -0.0064 -0.5037 -0.3857 -0.3298
-0.3586 0.2461 0.8622 -0.1458 0.0780 0.2002
-0.2925 -0.4033 -0.2275 -0.1038 0.4360 0.7065
-0.2078 0.6700 -0.3951 -0.5888 0.0260 0.0667
-0.5099 0.0597 -0.1097 0.2869 0.5946 -0.5371
-0.5316 0.1887 -0.1914 0.5341 -0.5485 0.2429
S =
17.7139 0 0 0
0 6.3917 0 0
0 0 3.0980 0
0 0 0 1.3290
0 0 0 0
0 0 0 0
Vtranspose =
-0.5710 -0.2228 0.6749 0.4109
-0.4275 -0.5172 -0.6929 0.2637
-0.3846 0.8246 -0.2532 0.3286
-0.5859 0.0532 0.0140 -0.8085
分解矩阵之后我们首先需要明白S的意义。
可以看到S很特别,是个对角线矩阵。
每个元素非负,而且依次减小,具体要讲明白元素值的意思大概和线性代数的特征向量,特征值有关。
但是可以大致理解如下:
在线性空间里,每个向量代表一个方向。
所以特征值是代表该矩阵向着该特征值对应的特征向量的方向的变化权重。
所以可以取S对角线上前k个元素。
当k=2时候即将S(6*4)降维成S(2*2),
同时U(6*6),Vtranspose(4*4)相应地变为 U(6*2),Vtranspose(4*2).
如下图(图片里的usv矩阵元素值和我自己matlab算出的usv矩阵元素值有些正负不一致,但是本质是相同的):

此时我们用降维后的U,S,V来相乘得到A2
A2=U(1:6,1:2)*S(1:2,1:2)*(V(1:4,1:2))' //matlab语句
A2 =
5.2885 5.1627 0.2149 4.4591
3.2768 1.9021 3.7400 3.8058
3.5324 3.5479 -0.1332 2.8984
1.1475 -0.6417 4.9472 2.3846
5.0727 3.6640 3.7887 5.3130
5.1086 3.4019 4.6166 5.5822
此时我们可以很直观地看出,A2和A很接近,这就是之前说的降维可以看成一种数据的有损压缩。
接下来我们开始分析该矩阵中数据的相关性。
我们将u的第一列当成x值,第二列当成y值。即u的每一行用一个二维向量表示,同理v的每一行也用一个二维向量表示。
如下图:

从图中可以看出:
Season5,Season6特别靠近。Ben和Fred也特别靠近。
同时我们仔细看一下A矩阵可以发现,A矩阵的第5行向量和第6行向量特别相似,Ben所在的列向量和Fred所在的列向量也特别相似。
所以从直观上我们发现U矩阵和V矩阵可以近似来代表A矩阵,换据话说就是将A矩阵压缩成U矩阵和V矩阵,至于压缩比例得看当时对S矩阵取前k个数的k值是多少。
到这里,我们已经完成了一半。
寻找相似用户:
依然用实例来说明:
我们假设,现在有个名字叫Bob的新用户,并且已知这个用户对season n的评分向量为:[5 5 0 0 0 5]。(此向量为列向量)
我们的任务是要对他做出个性化的推荐。
我们的思路首先是利用新用户的评分向量找出该用户的相似用户。

如上图(图中第二行式子有错误,Bob的转置应为行向量)。
对图中公式不做证明,只需要知道结论,结论是得到一个Bob的二维向量,即知道Bob的坐标。
将Bob坐标添加进原来的图中:

然后从图中找出和Bob最相似的用户。
注意,最相似并不是距离最近的用户,这里的相似用余弦相似度计算。(关于相似度还有很多种计算方法,各有优缺点)
即夹角与Bob最小的用户坐标。
可以计算出最相似的用户是ben。
接下来的推荐策略就完全取决于个人选择了。
这里介绍一个非常简单的推荐策略:
找出最相似的用户,即ben。
观察ben的评分向量为:【5 5 3 0 5 5】。
对比Bob的评分向量:【5 5 0 0 0 5】。
然后找出ben评分过而Bob未评分的item并排序,即【season 5:5,season 3:5】。
即推荐给Bob的item依次为 season5 和 season3。
最后还有一些关于整个推荐思路的可改进的地方:
1.
svd本身就是时间复杂度高的计算过程,如果数据量大的情况恐怕时间消耗无法忍受。
不过可以使用梯度下降等机器学习的相关方法来进行近似计算,以减少时间消耗。
2.
相似度计算方法的选择,有多种相似度计算方法,每种都有对应优缺点,对针对不同场景使用最适合的相似度计算方法。
3.
推荐策略:首先是相似用户可以多个,每个由相似度作为权重来共同影响推荐的item的评分。
-----------------------------------------------------------------------------------------------------------------------------------------------------
3. FMF 概率矩阵分解:
为了方便介绍,假设推荐系统中有用户集合有6个用户,即U={u1,u2,u3,u4,u5,u6},项目(物品)集合有7个项目,即V={v1,v2,v3,v4,v5,v6,v7},用户对项目的评分结合为R,用户对项目的评分范围是[0, 5]。R具体表示如下:
推荐系统的目标就是预测出符号“?”对应位置的分值。推荐系统基于这样一个假设:用户对项目的打分越高,表明用户越喜欢。因此,预测出用户对未评分项目的评分后,根据分值大小排序,把分值高的项目推荐给用户。怎么预测这些评分呢,方法大体上可以分为基于内容的推荐、协同过滤推荐和混合推荐三类,协同过滤算法进一步划分又可分为基于基于内存的推荐(memory-based)和基于模型的推荐(model-based),本文介绍的矩阵分解算法属于基于模型的推荐。
矩阵分解算法的数学理论基础是矩阵的行列变换。在《线性代数》中,我们知道矩阵A进行行变换相当于A左乘一个矩阵,矩阵A进行列变换等价于矩阵A右乘一个矩阵,因此矩阵A可以表示为A=PEQ=PQ(E是标准阵)。
矩阵分解目标就是把用户-项目评分矩阵R分解成用户因子矩阵和项目因子矩阵乘的形式,即R=UV,这里R是n×m, n =6, m =7,U是n×k,V是k×m。直观地表示如下:
高维的用户-项目评分矩阵分解成为两个低维的用户因子矩阵和项目因子矩阵,因此矩阵分解和PCA不同,不是为了降维。用户i对项目j的评分r_ij =innerproduct(u_i, v_j),更一般的情况是r_ij =f(U_i, V_j),这里为了介绍方便就是用u_i和v_j内积的形式。下面介绍评估低维矩阵乘积拟合评分矩阵的方法。
首先假设,用户对项目的真实评分和预测评分之间的差服从高斯分布,基于这一假设,可推导出目标函数如下:
最后得到矩阵分解的目标函数如下:
从最终得到得目标函数可以直观地理解,预测的分值就是尽量逼近真实的已知评分值。有了目标函数之后,下面就开始谈优化方法了,通常的优化方法分为两种:交叉最小二乘法(alternative least squares)和随机梯度下降法(stochastic gradient descent)。
首先介绍交叉最小二乘法,之所以交叉最小二乘法能够应用到这个目标函数主要是因为L对U和V都是凸函数。首先分别对用户因子向量和项目因子向量求偏导,令偏导等于0求驻点,具体解法如下:
上面就是用户因子向量和项目因子向量的更新公式,迭代更新公式即可找到可接受的局部最优解。迭代终止的条件下面会讲到。
接下来讲解随机梯度下降法,这个方法应用的最多。大致思想是让变量沿着目标函数负梯度的方向移动,直到移动到极小值点。直观的表示如下:
其实负梯度的负方向,当函数是凸函数时是函数值减小的方向走;当函数是凹函数时是往函数值增大的方向移动。而矩阵分解的目标函数L是凸函数,因此,通过梯度下降法我们能够得到目标函数L的极小值(理想情况是最小值)。
言归正传,通过上面的讲解,我们可以获取梯度下降算法的因子矩阵更新公式,具体如下:
(3)和(4)中的γ指的是步长,也即是学习速率,它是一个超参数,需要调参确定。对于梯度见(1)和(2)。
下面说下迭代终止的条件。迭代终止的条件有很多种,就目前我了解的主要有
1) 设置一个阈值,当L函数值小于阈值时就停止迭代,不常用
2) 设置一个阈值,当前后两次函数值变化绝对值小于阈值时,停止迭代
3) 设置固定迭代次数
另外还有一个问题,当用户-项目评分矩阵R非常稀疏时,就会出现过拟合(overfitting)的问题,过拟合问题的解决方法就是正则化(regularization)。正则化其实就是在目标函数中加上用户因子向量和项目因子向量的二范数,当然也可以加上一范数。至于加上一范数还是二范数要看具体情况,一范数会使很多因子为0,从而减小模型大小,而二范数则不会它只能使因子接近于0,而不能使其为0,关于这个的介绍可参考论文Regression Shrinkage and Selection via the Lasso。引入正则化项后目标函数变为:
(5)中λ_1和λ_2是指正则项的权重,这两个值可以取一样,具体取值也需要根据数据集调参得到。优化方法和前面一样,只是梯度公式需要更新一下。
矩阵分解算法目前在推荐系统中应用非常广泛,对于使用RMSE作为评价指标的系统尤为明显,因为矩阵分解的目标就是使RMSE取值最小。但矩阵分解有其弱点,就是解释性差,不能很好为推荐结果做出解释。
----------------------------------------------------------------------
概率的角度来预测用户的评分,本文假设用户和商品的特征向量矩阵都符合高斯分布,基于这个假设,用户对商品的喜好程度就是一系列概率的组合问题,例如
其中
为期望为μ,方差为σ的高斯分布。Iij=1,如果用户i选择了商品j,否则为0。在此基础上,本文通过对用户的特征向量加以限制,提出了一种新的算法,并且该算法要好于上述提到的算法。
方法:
首先,本文假设预测用户的喜好是一个概率组合问题:
其中用户和商品的特征向量都符合高斯分布:
对上述的预测公式取对数,我们可以得到
优化公式(3)等同于直接优化下列的公式
为了把评分(例如1-5的评分)转换为0-1,本文采用了如下办法:
因此对应的预测公式变为
另外本文通过对用户的特征向量加以限制,即
那么对应的评分预测函数为
其中W为某种权重矩阵,例如可以是相似度矩阵等等,同样的,W也符合高斯分布
实验结果:
上图是本文算法与Netflix系统推荐算法,SVD算法的对比结果。首先,SVD算法overfit比较严重,当epoch超过10时,SVD算法就开始overfit了,其次constrained PMF要好于PMF算法,而且该算法比Netflix系统推荐算法精度高7%左右。
另外本文也对比了,不同评分数目的RMSE的精度,如下图所示:
可以看出,当评分比较少的时候,constrained PMF算法的准确性就更加明显,另外,如果采用电影的平均分来作为用户的预测分值,当评分比较少的情况,这种算法跟PMF和constrained PMF算法差别不大,但是当评分比较多时,算法的准确性差异就很明显了
________________________________________________________________________________________________
4. 其他情况:
由于评分矩阵的稀疏性(因为每一个人只会对少数的物品进行评分),因此传统的矩阵分解技术不能完成矩阵的分解,即使能分解,那样计算复杂度太高,不现实。因此通常的方法是使用已存在评分计算出出预测误差,然后使用梯度下降调整参数使得误差最小。
首先说明一些符号的含义:戴帽子的rui表示预测u对i的打分,qi表示物品i每个特性的归属度向量,pu表示用户u对每个特性的喜欢程度的向量。因此,物品的预测得分为:
下面我们就需要根据已有的数据计算误差并修正q和p使得误差最小,误差的表示方式如下: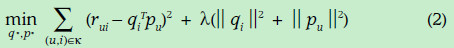
(2)式子可以利用评分矩阵中存在的评分数据,使用随机梯度下降方法进行参数的优化,在此不做介绍。注意第二项是正则式,是为了防止过拟合,具体原理也不太清楚。
计算完阐述后们对于未知的项目就可以使用(1)式子评分。
上面的式子是最基本的矩阵分解思想,但实际情况下,却并不是很好的衡量标准,比如有的网站中的用户偏向评价高分;有一些用户偏向评价高分(有的人比较宽容);有的物品被评价的分数偏高(也许由于等口碑原因)。因此在上面的式子中一般都会加入偏置项,u,bi,bu。综合用下面的式子表示
结果预测式子变成如下:
误差预测变成如下形式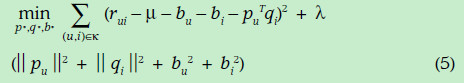
由于现实的评分矩阵特别稀疏,因此,为了使得数据更加稠密,下面加入了历史的引述反馈数据(比如用户浏览过浏览过某个电影就可以当做一定成的喜爱的正反馈),隐式反馈表现出来的偏好用下面的式子表示,其中xi表示历史数据所表现出的偏好的向量,跟前面的向量维度相同。前面的权重表示这一项的可信任程度。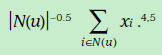
同样,我们也可以使用用户的标签(比如年龄,性别,职业)推测用户对每个因素的喜爱程度,形式化如下,ya表示标签所表现出的偏好向量。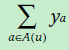
加入上面因素后的评分估计表示如下: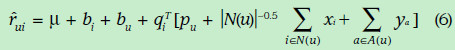
带有时间因素的矩阵分解
现实生活中,我们每个人的爱好可能随着时间的改变而改变,每个项目的平均评分也会改变。因此,项目的偏差(即项目高于平均分还是低于平均分)bi,用户的评分习惯(即偏向于高分还是低分)bu,以及用户的喜好矩阵pu都是时间的函数。为了更加准确的表达评分,都需要表示成为时间的函数形式,如下(这里没有考虑历史标签等数据):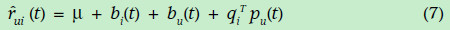
- 数据挖掘基础知识-矩阵(分解)
- 数据挖掘基础知识-矩阵(分解)
- 数据挖掘算法-矩阵分解在推荐系统中的应用
- 数据挖掘 基础知识 收集
- 数据挖掘之基础知识
- 数据挖掘基础知识
- 数据挖掘必备基础知识
- 数据挖掘必备基础知识
- 写给新人数据挖掘基础知识介绍
- 数据挖掘中的矩阵基础(1)
- 数据挖掘中的矩阵基础(2)
- 矩阵分解
- 矩阵分解
- 矩阵分解
- 矩阵分解
- 矩阵分解
- 矩阵分解
- 矩阵分解
- 非负谱分析用于特征选择
- 《云计算架构技术与实践》连载(16):2.4云计算解决方案典型架构组合及落地应用场景之2.4.1桌面云
- HCI层数据包格式
- 《云计算架构技术与实践》连载17:2.4.2 存储云
- 满足条件的整数
- 数据挖掘基础知识-矩阵(分解)
- 计算机原理学习 -- 操作系统发展和程序编译
- 《云计算架构技术与实践》连载18:2.4.3 IDC托管云
- OJ刷题之《函数模板--求n个数之和》
- 关于双向链表的理解
- hdu1506 Largest Rectangle in a Histogram (单调栈)
- UI:UIToolBar的使用
- HTTP Live Streaming直播(iOS直播)技术分析与实现
- Android OTA查分包打包方法






















