监督学习应用与梯度下降

 

文章转载自http://blog.sina.com.cn/s/blog_8e6f1b330101eu3b.html

 

监督学习：告诉算法每个样本的正确答案，学习后的算法对新的输入也能输入正确的答案 。监督指的是在训练样本答案的监督下。

1、 线性回归

例：Alvin汽车，先让人开车，Alvin摄像头观看（训练），而后实现自动驾驶。

本质是一个回归问题，汽车尝试预测行驶方向。

 

例：上一节课的房屋大小与价格数据集

 

引入通用符号：

m = 训练样本数

x = 输入变量（特征）

y = 输出变量（目标变量）

(x,y) – 一个样本

 –第i个训练样本=

 

本例中：m：数据个数，x：房屋大小，y：价格

 

监督学习过程：

1)      将训练样本提供给学习算法

2)      算法生成一个输出函数（一般用h表示，成为假设）

3)      这个函数接收输入，输出结果。（本例中为，接收房屋面积，输出房价）将x映射到y。

如下图所示：

 

 

 

对假设进行线性表示：

 

通常来说，回归问题有多个输入特征。如上例中，我们还已知房屋的卧室数，即有个第二个特征。即表示大小，表示卧室数，则可将假设写成：

 

为了将公式写整洁，定义，则h可写成：

n = 特征数目， ：参数

 

选择的目的，是使h(x)与y的平方差尽量小。又由于有m个训练样本，需要计算每个样本的平方差，最后为了简化结果乘以1/2，即：（最小二乘法的思想，使得预测数据尽量接近训练集给出的答案，剩下的问题是求该函数的最小值时的值。）

我们要做的就是求：min(J())

求min(J())方法：梯度下降和正规方程组

 

2、 梯度下降

梯度下降是一种搜索算法，基本思想：先给出参数向量一个初始值，比如0向量；不断改变，使得J()不断缩小。

维基百科梯度下降法（http://zh.wikipedia.org/wiki/最速下降法）梯度下降法，基于这样的观察：如果实值函数 在点 处可微且有定义，那么函数 在 点沿着梯度相反的方向 下降最快。

因而，如果

对于 为一个够小数值时成立，那么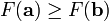

有关梯度的知识参加《高等数学第六版下册（同济大学）》P101

因此沿梯度反方向函数J（ ）减小的最快，以快速收敛到最小值。

改变 的方法：梯度下降

如图所示，水平坐标轴表示，垂直坐标表示J()

 

一开始选择0向量作为初始值，假设该三维图为一个三维地表，0向量的点位于一座“山”上。梯度下降的方法是，你环视一周，寻找下降最快的路径，即为梯度的方向，每次下降一小步，再环视四周，继续下降，以此类推。结果到达一个局部最小值，如下图：

 

 

当然，若初始点不同，则结果可能为另一个完全不同的局部最小值，如下：

 

表明梯度下降的结果依赖于参数初始值。

 

梯度下降算法的数学表示：

 

 为赋值运算符，即表示程序中的的赋值语句。

每一次将减去对求偏导的结果，即沿最陡峭的“山坡”下降（梯度反方向，函数J（）减小的最快）；

 

针对一组训练数据，将偏导数展开分析：

（PS：把后面的（h（x）-y）视为一个整体）;

 

代入上式：

 

 

：学习速度，步长，手动给出的参数。即决定你下山时每一步迈多大。设的过小，收敛时间长，设的过大，可能会超过最小值

 

（1）     批梯度下降算法：

上述为处理一个训练样本的公式，将其派生成包含m个训练样本的算法，循环下式直至收敛：

 

复杂度分析：

对于每个的每次迭代，即上式所示，时间为O(m)

每次迭代（走一步）需要计算n个特征的梯度值，复杂度为O(mn)

 

一般来说，这种二次函数的的三维图形为一个碗状，有一个唯一的全局最小值。其等高线为一个套一个的椭圆形，运用梯度下降会快速收敛到圆心。

 

梯度下降性质：接近收敛时，每次的步子会越来越小。其原因是每次减去乘以梯度，但是梯度会越来越小，所以步子会越来越小。

 

下图为使用梯度下降拟合的上例房屋大小和价格的曲线

 

检测是否收敛的方法：

1)      检测两次迭代的改变量，若不再变化，则判定收敛

2)      更常用的方法：检验，若不再变化，判定收敛

 

批梯度下降算法的优点是能找到局部最优解，但是若训练样本m很大的话，其每次迭代都要计算所有样本的偏导数的和，当训练集合数据量大时效率比较低，需要的时间比较长，于是采用下述另一种梯度下降方法。

 

（2）     随机梯度下降算法（增量梯度下降算法）：

 

每次计算不需要再遍历所有数据，而是只需计算样本i即可。

即批梯度下降中，走一步为考虑m个样本；随机梯度下降中，走一步只考虑1个样本。

每次迭代复杂度为O(n)。当m个样本用完时，继续循环到第1个样本。

增量梯度下降算法可以减少大训练集收敛的时间（比批量梯度下降快很多），但可能会不精确收敛于最小值而是接近最小值。

上述使用了迭代的方法求最小值，实际上对于这类特定的最小二乘回归问题，或者普通最小二乘问题，存在其他方法给出最小值，接下来这种方法可以给出参数向量的解析表达式，如此一来就不需要迭代求解了。

 

3、 正规方程组

给定一个函数J，J是一个关于参数数组的函数，定义J的梯度关于的导数，它自己也是一个向量。向量大小为n+1维（从0到n），如下：

所以，梯度下降算法可写成：

J：关于参数数组的函数；

下三角：梯度

更普遍的讲，对于一个函数f，f的功能是将一个m*n的矩阵映射到实数空间上，即：

假设输入为m*n大小的矩阵A，定义f关于矩阵A的导数为：

导数本身也是个矩阵，包含了f关于A的每个元素的偏导数。

 

如果A是一个方阵，即n*n的矩阵，则将A的迹定义为A的对角元素之和，即：

 

trA即为tr(A)的简化。迹是一个实数。

 

一些关于迹运算符和导数的定理：

1)      trAB = trBA

2)      trABC = trCAB = trBCA

3)      

4)      

5)      若，tra = a

6)      

  

有了上述性质，可以开始推导了：

定义矩阵X，称为设计矩阵，包含了训练集中所有输入的矩阵，第i行为第i组输入数据，即：

则由于，所以可得：

又因为对于向量z，有，则有：

由上述最后一个性质可得：

通过上述6个性质，推导：

倒数第三行中，运用最后一个性质

 

将置为0，则有：

称为正规方程组

可得：（推导过程知识：迹与矩阵求导）