理解迭代法和优化基础

后面介绍的时候结合另一个博客的内容：

http://blog.csdn.net/zouxy09/article/details/8537872

     

    个人理解因为其实无论什么机器学习算法，最终都要求助于计算机解决，它又表现为在特定函数空间按某优化目标去搜索一个解出来。衡量指标就有误差最小还是性能指标最大吧？那你怎么求它的最小还是最大呢？求导，有拉格朗日？是没错，但他们能使用的本质条件是什么？是这些误差函数或者性能函数有解析式的时候。但是世界很多信号都是非平稳的，或者很难知道其统计特性的，这时候就没法得到其准确的解析式了，那这时候怎么找最大或者最小值啊。迭代？什么是迭代？

     这里就这涉及到找最大值和最小值，梯度就是类似于在等高线的位置的垂直方向是上升或者下降最块的方向，沿着这个方向最快达到最大最小值，每一次走的距离就是步长，这里就是梯度上升和梯度下降的算法。一般最小化损失函数利用梯度下降，最大化似然概率利用梯度上升，上升的方法可以类似概率论统计理论。但是如果处理非线性的复杂问题，梯度上升，下降可以带来以下几种情况：

1 靠近极值点的时候迭代次数变慢

2 出现Z字形变化

     如果你在山脚，看到了山顶，你就不管三七二十一了，直接就往山顶那个方向不要命的冲，直到到达山顶。这个

就是牛顿迭代法。

 在数学的含义中可以参见博客：http://www.cnblogs.com/houkai/p/3332520.html

总结来说就是：

要求一个f(x) = 0，首先确定一个初始的解x0，然后获得一个迭代方程，通过Xn-1推导出Xn，然后当这两个值得误差小于一定得数据的时候就可以判断为收敛

在确定收敛方程的时候，有两种思路：一个是利用一阶泰勒展开，一个是几何上的求切线的方法

 如下图，已知(x0,y0) ,我们通过对f(x0)做切线，得到切线与x轴的交点(x1,0)，然后根据(x1,f(x1))继续递推得到(x2,f(x2))：

                                      

 那么对已知的(x0,y0)，我们可以得到斜率：f'(x0)和点(x0,y0)，那么我们可以得到直线：y-f(x0)=f'(x0)(x-x0)。再令y=0，我们可以得到：f(x)=x0-f(x0)/f'(x0)。其实我们已经得到了与泰勒级数展开相同的迭代公式。

对初值的选取要求较高。一般的，Newton迭代法只有局部收敛性，当初值在收敛区间里时，收敛速度很快(平方收敛)。但初值离方程根x*较远时，不能保证Newton迭代法收敛。

这里为了使Xn能够更快进入收敛区间有牛顿下山法

 称为下山因子

具体做法如下：

1. 选取初值 
2. 取下山因子（可修改） 
3. 计算 
4. 计算并比较与的大小： 
若，则 
         1） 当时，取，结束； 
         2） 当时，将作为新的值继续计算； 
若，则取，返回3。

下面结合介绍牛顿法用于最优化的问题：

在最优化的问题中，线性最优化至少可以使用单纯行法求解，但对于非线性优化问题，牛顿法提供了一种求解的办法。假设任务是优化一个目标函数f，求函数f的极大极小问题，可以转化为求解函数f的导数f'=0的问题，这样求可以把优化问题看成方程求解问题（f'=0）。剩下的问题就和第一部分提到的牛顿法求解很相似了。

这次为了求解f'=0的根，把f（x）的泰勒展开，展开到2阶形式：

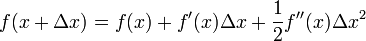
这个式子是成立的，当且仅当 Δx 无线趋近于0。此时上式等价与：

求解：

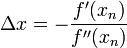
得出迭代公式：

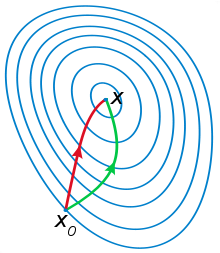
一般认为牛顿法可以利用到曲线本身的信息，比梯度下降法更容易收敛（迭代更少次数），如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。

在上面讨论的是2维情况，高维情况的牛顿迭代公式是：

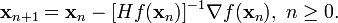
其中H是hessian矩阵，定义为：

 

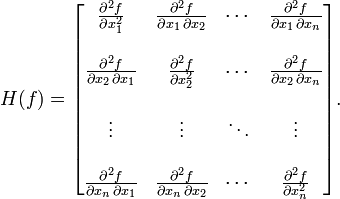
高维情况依然可以用牛顿迭代求解，但是问题是Hessian矩阵引入的复杂性，使得牛顿迭代求解的难度大大增加，但是已经有了解决这个问题的办法就是Quasi-Newton methond，不再直接计算hessian矩阵，而是每一步的时候使用梯度向量更新hessian矩阵的近似。

如果你在山脚开始，每爬一小段，然后下一步的方向你就随便蒙，听天由命，因为你相信，上帝会把你带到山顶的（上帝就是那个操纵概率的手），这个就是随机搜索算法。

       好了，当你历经千辛万苦爬上一个山顶的时候，发现还有更高的山顶，但没办法啊，如果想到那个更高的山顶，你就得先下坡，再爬上那个山顶。这时候，有些人就满足了，看到了他想看到的美景，乐于他的局部最大值，不想折腾了。但有些人就不满足，你渴望那种“山顶绝顶我为峰，一览众山小”的心境，所以你就纵身一跳，滚到了山脚，如果你好运，那你就滚到了那个最高山顶的山脚，这时候，你再往上爬，就可以到达最高峰了。这个就是避免陷于局部最大值，寻找全局最大值的算法，叫模拟退火或者冲量等等。

爬山法是完完全全的贪心法，每次都鼠目寸光的选择一个当前最优解，因此只能搜索到局部的最优值。模拟退火其实也是一种贪心算法，但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以图1为例，模拟退火算法在搜索到局部最优解A后，会以一定的概率接受到E的移动。也许经过几次这样的不是局部最优的移动后会到达D点，于是就跳出了局部最大值A。

模拟退火算法描述：

         若J( Y(i+1) )>= J( Y(i) )  (即移动后得到更优解)，则总是接受该移动

         若J( Y(i+1) )< J( Y(i) )  (即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）

　　这里的“一定的概率”的计算参考了金属冶炼的退火过程，这也是模拟退火算法名称的由来。

　　根据热力学的原理，在温度为T时，出现能量差为dE的降温的概率为P(dE)，表示为：

　　　　P(dE) = exp( dE/(kT) )

　　其中k是一个常数，exp表示自然指数，且dE<0。这条公式说白了就是：温度越高，出现一次能量差为dE的降温的概率就越大；温度越低，则出现降温的概率就越小。又由于dE总是小于0（否则就不叫退火了），因此dE/kT < 0 ，所以P(dE)的函数取值范围是(0,1) 。

　　随着温度T的降低，P(dE)会逐渐降低。

　　我们将一次向较差解的移动看做一次温度跳变过程，我们以概率P(dE)来接受这样的移动。

　　关于爬山算法与模拟退火，有一个有趣的比喻：

　　爬山算法：兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法，它不能保证局部最优值就是全局最优值。

　　模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向高处，也可能踏入平地。但是，它渐渐清醒了并朝最高方向跳去。这就是模拟退火。

模拟退火算法是一种随机算法，并不一定能找到全局的最优解，可以比较快的找到问题的近似最优解。 如果参数设置得当，模拟退火算法搜索效率比穷举法要高。
总结出寻找最优值的三个主要因素是：

1 迭代方向

2 迭代步长

3 局部最大或者是全局最大，其中的转化代价有多大

下面补充讲解一些基础知识：

http://blog.csdn.net/china1000/article/details/38969181

小总结就是：

  1.  凸函数：

              凸函数有很多优良的特性，而且在求解极大值极小值时，十分有用。先看一下凸函数的定义：凸函数：在函数的区间I上，若对任意x1和x2，任意0<t<1，都有

                                    

             或者对任意x1,x2都有：

                                  

             凸函数有很多优良的：

                        1. 凸函数任何极小值也是最小值。

                        2. 一元二阶的函数在区间上是凸的，当且仅当它的二阶倒数是非负的；如果一个函数的二阶导数是正数，那么函数也就是严格凸的。反过来不成立。多元二次可微的连续函数在凸集上是可微的，当且仅当它的hessian矩阵在凸集内部是半正定的（这里还不是很理解，还需要继续加强）。

                        3.   对于凸函数f，水平子集{x| f(x) <=a}和{x|f(x)<=a}是凸集。然而，水平子集是凸集的函数不一定是凸函数；这样的函数被称为拟凸函数。

                        4.  凸函数的求和、最大也是凸函数；如果g(x)是递增的，那么g(f(x))仍然是凸函数。

    2.  hessian矩阵：

              hessian(海瑟矩阵)就是所谓的二阶偏倒矩阵。对于一个临界点有一阶偏导等于零，然而凭借一阶偏导数无法确定这个点是鞍点、局部极大点还是局部极小点。而hessian矩阵可以回答这个问题。

                             

             若x0是f(x)的极值点，如果存在，则进一步设在一个邻域内所有二阶导数连续，H为在点x0的海瑟矩阵。而且

x0是f(x)的极小值点时H>=0，即H的特征根均为非负

x0是f(x)的极大值点，H<=0, 即H的特征根均为非负

H>0，即H为正定矩阵，x0是f(x)的极小值点

H<0，即H为负定矩阵，x0是f(x)的极大值点；

H的特征值有正有负，x0不是f(x)的极值点。

    3.  正定矩阵：

             设M是n阶方阵，如果对任何非零变量z，都有z'Mz>0,其中z'表示z的转置，就称M正定矩阵。

             判定定理1：矩阵A的特征值全为正。

             判定定理2：A的各阶主子式为正。

             判定定理3：A合同于单位阵。

    4.  泰勒展开：

             泰勒公式可以用若干项加一起来表示一个函数。对于正整数n，若函数f(x)在闭区间[a,b]上n阶可导，切在(a,b)上面n+1阶可导数。任取a<=x<=b，则有：

             

            拉格朗日余数：

            

            请注意：泰勒展开在很多地方都有重要的应用，例如开方的计算。这里添加上牛顿迭代和泰勒级数展开求解根号的计算过程。另外我一直以为泰勒级数和牛顿迭代有一定关系，后来发现好像没有，不过可以把牛顿迭代看做仅取泰勒级数的一阶展开。

            1). 使用泰勒级数求解根号2。此时我们可以得到f(x)=x^2-2;

                        取泰勒级数前两项，我们可以得到： f(x)=f(a) + f'(a)(x-a)，令f(x)=0我们可以得到：

                         x=a-f(a)/f'(a); 其实我们可以把x看做是f(x)=0的解，使用这个式子多次迭代就可以得到根号的值。使用x(n+1)替换x，x(n)替换a，我们就可以得到：x(n+1)=x(n)-f(x(n))/f'(x(n))=x(n)-(x(n)^2-2)/2*x(n).

            2). 牛顿迭代法：

                      

     5.  拉格朗日乘子：

             拉格朗日乘子，就是求函数f(x1,x2,....)在g(x1,x2,....)=0的约束条件下的极值的方法。主要思想是通过引入一个新的参数λ，将约束条件和原函数联系到一起，从而求出原函数极值的各个变量的解。假设需要求极值的目标函数f(x,y)，约束条件为φ(x,y)=M，然后我们得到新的函数： F(x,y,λ)=f(x,y)+λg(x,y)，将新函数分别对x,y, λ求解即可得到原函数的极值。