程序博客网 > mac怎么解压zip

蓝桥杯结果填空正六面体染色 Burnside引理

来源：互联网发布：mac怎么解压zip 编辑：程序博客网时间：2024/04/28 14:51

正六面体用4种颜色染色。

共有多少种不同的染色样式？

要考虑六面体可以任意旋转、翻转。

参考答案：

240

可以想象，这道题如果编程的话，代码不会很少，关键是也没啥思路，其实组合数学早就给我们提供了数学工具，就是burnside引理（已下内容参考维基百科）

伯恩赛德引理

伯恩赛德引理（Burnside's lemma），也叫伯恩赛德计数定理（Burnside's counting theorem），柯西-弗罗贝尼乌斯引理（Cauchy-Frobenius lemma）或轨道计数定理（orbit-counting theorem），是群论中一个结果，在考虑对称的计数中经常很有用。该结论被冠以多个人的名字，其中包括威廉·伯恩赛德（William Burnside）、波利亚、柯西和弗罗贝尼乌斯。这个命题不属于伯恩赛德自己，他只是在自己的书中《有限群论 On the Theory of Groups of Finite Order》引用了，而将其归于弗罗贝尼乌斯 (1887)^[1]。

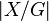下文中，设 $G$ 是一个有限群，作用在集合 $X$ 上。对每个 $g$ 属于 $G$ 令 $X^g$ 表示 $X$ 中在 $g$ 作用下的不动元素。伯恩赛德引理断言轨道数（记作 $|X/G|$ ）由如下公式给出：^[2]

|X/G| = \frac{1}{|G|}\sum_{g \in G}|X^g|.\,

从而轨道数（是一个自然数或无穷）等于被 G 中一个元素保持不动的点个数的平均值（故同样是自然数或无穷）。

也许你并没有看懂到底说的是什么，其实我也看不大懂，群这一部分是在离散数学中学过，不过不是很详细，有个大概的概念，我们需要知道的是下面这个应用：

使用三种颜色对立方体的面染色，旋转后相同的视为一种，染色方式总数可以由这个公式确定。

选取一个定向，设 X 是这个定向立方体所有 3⁶ 种可能面染色组合，立方体的旋转群自然作用在 X 上。则 X 的两个元素属于同一轨道恰好是一个是另一个的旋转。旋转不同的染色数就是轨道数，可以通过数 G 的 24 个元素的不动集合的大小求出来。

这些自同构的详细检验可参见循环指标（Cycle index）一文。六个 90 度面旋转，每一个保持 X 的 3³ 个元素不变。
六个 90 度面旋转，每一个保持 X 的 3³ 个元素不变。
三个 180 度面旋转，每一个保持 X 的 3⁴ 个元素不变。
八个 120 度顶点旋转，每一个保持 X 的 3² 个元素不变。
六个 180 度边旋转，每一个保持 X 的 3³ 个元素不变。

这样，平均不动集合的大小是

\frac{1}{24}\left(3^6+6\times 3^3 + 3 \times 3^4 + 8 \times 3^2 + 6 \times 3^3 \right) = 57.\,

从而有 57 种旋转不同的立方体面 3 色染色方式。一般地，使用 n 种颜色，立方体不同的旋转面染色数是

\frac{1}{24}\left(n^6+3n^4 + 12n^3 + 8n^2\right).\,

<-----千百句话语就是这个公式，将4带入，就可以求出结果

证明

定理的证明利用轨道-中心化子定理以及 X 是轨道的不交并的事实：

\sum_{g \in G}|X^g| = |\{(g,x)\in G\times X \mid g\cdot x = x\}| = \sum_{x \in X} |G_x|

= \sum_{x \in X} \frac{|G|}{|Gx|} = |G| \sum_{x \in X}\frac{1}{|Gx|} = |G|\sum_{A\in X/G}\sum_{x\in A} \frac{1}{|A|}

= |G| \sum_{A\in X/G} 1 = |G| \cdot |X/G|.

0 0

mac怎么解压zip

mac怎么解压zip

原创粉丝点击

热门问题 老师的惩罚人脸识别我在镇武司摸鱼那些年重生之率土为王我在大康的咸鱼生活盘龙之生命进化天生仙种凡人之先天五行春回大明朝姑娘不必设防，我是瞎子康佳电视黑屏怎么办手机error错误怎么办 w10系统卡怎么办 w10系统投屏卡死怎么办 fifaol3停服怎么办幽灵行动死了怎么办 qq登录错误怎么办 qq为什么进不去怎么办全无敌中毒怎么办被执行人在国外怎么办 cass卸载不了怎么办萌钻激码忘了怎么办空中120怎么办保险电脑输入不支持怎么办罐子拧不开怎么办抓包之后怎么办 dnfclient不兼容怎么办 client.exe损坏怎么办爱拍充不进去电怎么办 dnf打团卡掉了怎么办上班总挨骂怎么办喜马拉雅被禁言怎么办褪黑素吃了头疼怎么办 dnf魔战没黄字怎么办喂奶期间痔疮怎么办哺乳期痔疮怎么办哺乳期得痔疮怎么办浦乳期得了痔疮怎么办哺乳期拉肚怎么办哺乳期腱鞘炎怎么办公户里的钱怎么办减肥停药后胸闷怎么办空投掉房顶怎么办空投挂树上怎么办经济危机时怎么办经济不好怎么办家里经济不好怎么办经济危机余额宝怎么办 2018通货膨胀钱怎么办不想实习怎么办遇见残疾乞丐怎么办