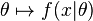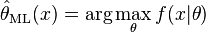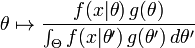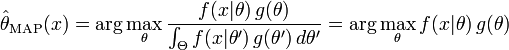特定条件下结构风险最小化等价于最大后验概率估计得证明
来源:互联网 发布:caffe安装windows 编辑:程序博客网 时间:2024/05/17 07:24
机器学习的三要素为模型、策略和算法。其中策略的两种是经验风险最小化和结构风险最小化。李航老师的《统计学习方法》第9页指出“当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时,结构风险最小化就等价于最大后验概率估计。”下面给出证明,不足不对的地方请指正。
首先给出最大后验概率的定义,引用维基百科对其的定义,有:
************************************************************
在贝叶斯统计学中,“最大后验概率估计”是后验概率分布的众数。利用最大后验概率估计可以获得对实验数据中无法直接观察到的量的点估计。它与最大似然估计中的经典方法有密切关系,但是它使用了一个增广的优化目标,进一步考虑了被估计量的先验概率分布。所以最大后验概率估计可以看作是规则化(regularization)的最大似然估计。
假设我们需要根据观察数据  估计没有观察到的总体参数
估计没有观察到的总体参数  ,让
,让  作为
作为  的采样分布,这样
的采样分布,这样 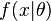 就是总体参数为
就是总体参数为  时
时  的概率。函数
的概率。函数
即为似然函数,其估计
就是  的最大似然估计。
的最大似然估计。
假设  存在一个先验分布
存在一个先验分布  ,这就允许我们将
,这就允许我们将  作为 贝叶斯统计(en:Bayesian statistics)中的随机变量,这样
作为 贝叶斯统计(en:Bayesian statistics)中的随机变量,这样  的后验分布就是:
的后验分布就是:
其中  是
是  的domain,这是贝叶斯定理的直接应用。
的domain,这是贝叶斯定理的直接应用。
最大后验估计方法于是估计  为这个随机变量的后验分布的众数:
为这个随机变量的后验分布的众数:
后验分布的分母与  无关,所以在优化过程中不起作用。注意当前验
无关,所以在优化过程中不起作用。注意当前验  是常数函数时最大后验估计与最大似然估计重合。
是常数函数时最大后验估计与最大似然估计重合。
************************************************************
我们对上式进行一些变换(先加上对数,再将对数展开),则上式等价于:
进一步的,有:
可以发现,等式右边第一部分刚好为最大似然估计的公式,我们将最大似然估计的公式写出:
将最大似然估计的公式代入,然后通过增加负号将最大后验概率分布公式的max改为min。这样,最大后验概率估计的公式可以写成下面这样:
对比结构风险最小化公式:
由于f( | )是模型,可以是条件概率分布模型,那么




- 特定条件下结构风险最小化等价于最大后验概率估计得证明
- 特定条件下经验风险最小化等价于极大似然估计的证明
- 特定条件下经验风险最小化等价于极大似然估计的证明(转载)
- 最大似然估计和最大后验概率估计
- 贝叶斯估计与结构风险最小化
- 最大后验概率估计算法
- 极大似然估计 最大后验概率估计
- 先验概率、后验概率与最大似然估计
- 先验概率、后验概率、最大似然估计
- 先验概率/后验概率/最大似然估计
- 通俗理解最大似然估计,最大后验概率估计,贝叶斯估计
- 先验概率、最大似然估计、贝叶斯估计、最大后验概率
- 先验概率、最大似然估计、贝叶斯估计、最大后验概率
- 最大似然估计和最大后验概率
- 最大似然估计和最大后验概率
- 最大似然估计和最大后验概率
- 最大似然估计与最大后验概率
- 极大似然估计,最大后验概率估计(MAP),贝叶斯估计
- SDOUG--Oracle山东用户组成立了
- ListView 中使用onItemClick和onItemLongClick
- HDU 4749 Parade Show Kmp
- Redis data types
- NSArray,NSSet,NSDictionary 对比总结
- 特定条件下结构风险最小化等价于最大后验概率估计得证明
- 在thinkphp3.2基础上封装上传图片接口
- 注解机制 androidannotations 让编程更随性,更轻松(一)
- 第六周项目一--深复制体验
- HDU 1016 Prime Ring Problem
- 【Cocos2d-x】截屏实现的两种方法RenderTexture和glReadPixel,实现和原理详细分析
- mcc函数实现matlab的m文件转化为c,c++文件。
- scanf()函数探究
- 设计模式之代理模式学习------强制代理-----------《设计模式之禅》学习笔记