分而治之策略
来源:互联网 发布:unity3d创建材质球 编辑:程序博客网 时间:2024/05/29 10:41
- 分而治之的概念
分而治之是一种使用递归解决问题的算法,主要的技巧是将一个大的复杂的问题划分为多个子问题,而这些子问题可以作为终止条件,或者在一个递归步骤中得到解决,所有子问题的解决结合起来就构成了对原问题的解决
2. 分而治之的优点和缺点
分而治之算法通常包括一个或者多个递归方法的调用,当这些调用将数据分隔成为独立的集合从而处理较小集合的时候,分而治之的策略将会有很高的效率,而在数据进行分解的时候,分而治之的策略可能会产生大量的重复计算,从而导致性能的降低。
3. 画标尺程序的分析讲解
画标尺是分而治之的策略的一个简单应用,标尺是由长度为1英寸的单元构成的序列,每个单元的末端有最长的记号,每个寸单元的1/2英寸处的记号要比末端的短,在1/4处的记号比1/2的要短,1/8处比1/4处短,编写一个程序,在一条线上,用规则间隔来绘制标记,在特定位置有特定大小的记号。
分析:在一个直线上,我们可以首先将这条直线一分为二,然后对分出来的二个再进行拆分。直到满足一定的精度要求,比如以最小刻度为1/8英寸为例,drawRuler作为画标尺的第归函数,在drawRuler函数中用一段线段的两端(起点(startPos),终点(endPos)),和变量h作为参数,标记的基础高度为baseHeight,
而标记的高度应该为h*baseHeight,则标尺的画法可以分析如下:
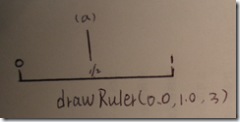
计算间隔(0.0,1.0)的中点:midPos = (startPost+endPos)/2;在中点1/2处画一个标记,高度为3*baseHeight
将中点分隔开的为两条直线,再使用第归函数drawRule,对应的起点,终点为(0.0,0.5)和(0.5,1.0),参数h-1,这样可以使高度相比短些
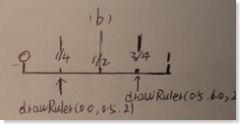
第归步骤2(h=2)
midPos = (0.0+0.5)/2 (1/4处),高度为 2*baseHeight
midPos = (0.5+1.0)/2 (3/4处)高度为 2*baseHeight
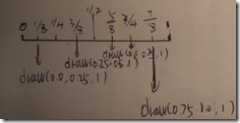
第归步骤(h=1)
分别在1/8处和7/8处标记,计算方法
midPos = (0.0+0.25)/2 (1/8) 高度为baseHeight
midPos = (0.75+1)/2 (7/8) 高度为baseHeight
用图示可以表示如下
我们可以将连续第归产生的记号看作二叉树的节点。树根h为初值。就是1/2处的记号,每个父记号都产生了两个子记号。如下图所示

void drawRuler(float startPos, float endPos, int h)
{
float baseHeight =4;
if (h > 0)
{
float midPos = (startPos + endPos) / 2;
float height = h * baseHeight;
drawMark(midPos, height);
drawRuler(startPos, midPos, h - 1);
drawRuler(midPos, endPos, h - 1);
}
}
void drawMark(float pos, float height)
{
Graphics g = this.CreateGraphics();
{
float xOffset = 100 + pos;
float yOffset = 100-height;
g.setColor(Color.RED);
g.DrawLine(p, xOffset, yOffset, xOffset, 100);
}
}
- 分而治之策略
- 分而治之策略及大数据处理实例讲解
- 分而治之
- 分而治之
- 分而治之
- 归并排序(mergeSort) 与 分而治之策略(divide and conquer)
- 大数据的处理策略,分而治之,多路归并
- 大数据的排序策略,分而治之,多路归并
- 递归策略(减而治之和分而治之)
- 快速排序(分而治之策略及C语言实现)
- 分而治之算法
- 分而治之算法
- 解决之道:分而治之
- 分而治之算法
- 编码 分而治之
- 2.分而治之
- 分而治之算法
- 算法中的分而治之思想
- Effective C++笔记_条款43 学习处理模板化基类内的名称
- Android-SharedPreference
- secureCRT和secureFX真的太方面了!!!
- [授权发表]开源书籍:《C语言编程透视》
- MPI、PThread笔记
- 分而治之策略
- java反射
- 最快最简单的排序---(初级)桶排序
- java编程思想学习
- 一步一步开发sniffer(Winpcap+MFC)(二)掀起你的盖头来,让我来画你的脸——用MFC开发GUI
- openGL ES
- 第六周(深复制)
- 排列组合算法的实现代码
- 两种日志方式


