抽样方法

来自于中科院《统计学习基础》研究生课程第9-13讲 [链接为课程课件与作业答案]
(http://www.jdl.ac.cn/user/lyqing/StatLearning/Statistical09Fall.html)
初学这块内容，若有不对，请多多指教！

1.已知概率密度函数且维数较低时，利用均匀分布直接产生任意分布的采样结果；
2.当密度函数未知且维数较低时，则可以采用基本蒙特卡罗方法、接受-拒绝方法和重要性采样来实现；
3.而维数很高的时候，则需要利用马尔可夫-蒙特卡罗(MCMC)实现，主要有Metropolis-Hasting algorithm(被誉为20世纪最杰出贡献的十大算法之一)、Gibbs算法等。

==================分割线=====================

1.概率积分变换方法

已知随机变量的概率密度函数，对任意分布采样，产生随机样本的步骤：
首先已知f(x)，求得F(x) -> F(x)的逆函数；
然后利用y~Uniform(0, 1)产生随机数y，带入F(x)逆函数中求解x
有效地利用均匀分布采样，得到任意分布采样的随机数。
缺陷：
1)必须已知概率密度函数PDF
2)随机变量的累积概率函数CDF及其逆函数invCDF可求

example 1

matlab code:

clear; clc;pd = makedist('Exponential', 'mu', 3);x = 0:0.1:26;y = cdf(pd, x);plot(x, y,  'r-', 'linewidth', 2)n = 100;yy = rand(n, 1);xx = icdf(pd, yy);hold onplot(xx, yy, 'bo', 'linewidth', 2)legend('original pdf', 'sampling points')

结果

2.basic monte carlo method

20世纪40年代，在冯·诺伊曼，斯塔尼斯拉夫·乌拉姆和尼古拉斯·梅特罗波利斯在洛斯阿拉莫斯国家实验室为核武器计划工作时，发明了蒙特卡罗方法。是一种以概率统计理论为指导的一类非常重要的数值计算方法。以赌城的名字–蒙特卡罗而被人熟记。

basic monte carlo method（蒙特卡罗）基本思想：利用大量采样的方法来求解一些难以直接计算得到的积分。而在连续随机变量中，CDF往往是通过PDF积分得到的，所以蒙特卡罗方法常被用于随机模拟采样中。

example 2：估算π值：假想你有一袋豆子，把豆子均匀地朝这个图形上撒，然后数这个图形之中有多少颗豆子，这个豆子的数目就是图形的面积。当你的豆子越小，撒的越多的时候，结果就越精确。借助计算机程序可以生成大量均匀分布坐标点，然后统计出图形内的点数，通过它们占总点数的比例和坐标点生成范围的面积就可以求出图形面积。
matlab code：

N = 30000;x = rand(1, N);y = rand(1, N);count = 0;for i = 1 : N    if (x(i)^2 + y(i)^2) <= 1        count = count + 1;    endendpi_my = 4 * count / N;error = abs(pi_my - pi) / pi;

实验结果：放置30000个随机点后,π的估算值与真实值相差0.07%.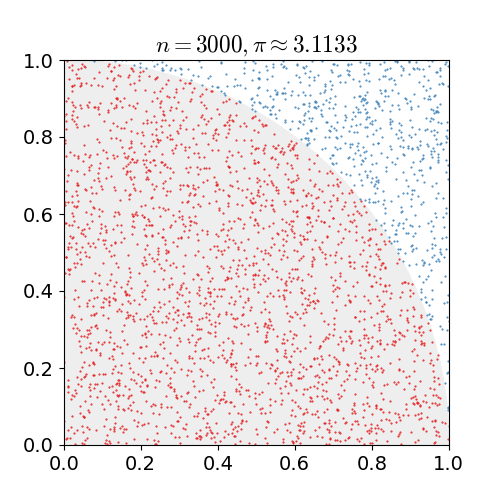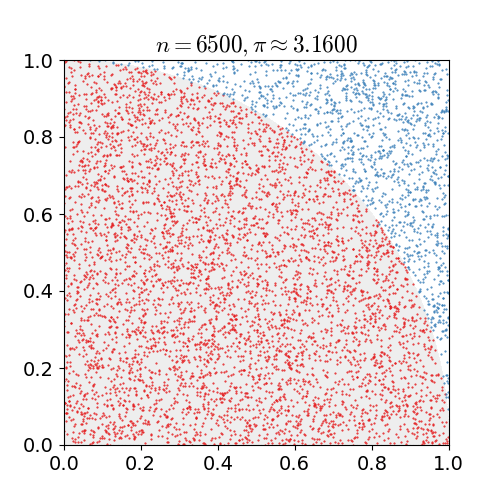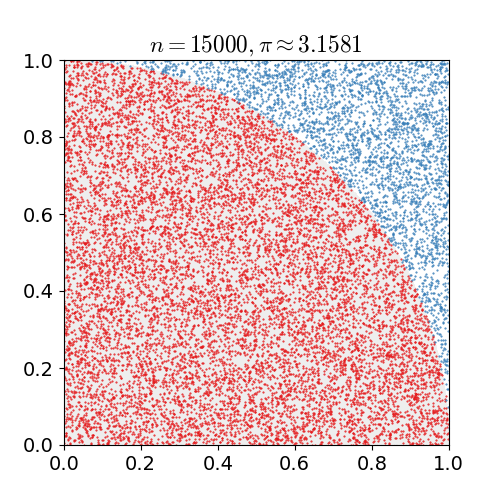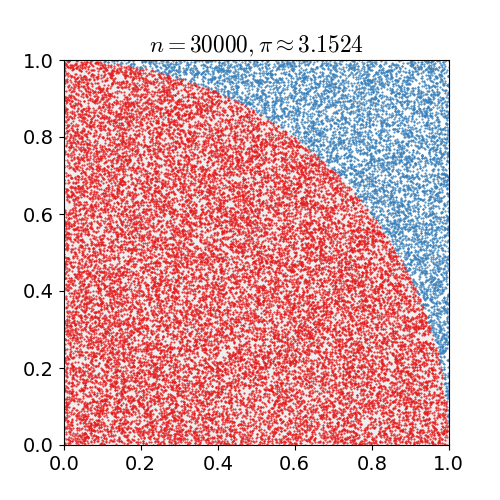

3.acceptance-rejection method

当随机变量的概率密度函数太复杂的时候，通常可以用建议分布来简化抽样过程

上图中p(z)（另一个课件中称为π(x)）是随机变量的PDF，q(z)是建议分布，利用建议分布逼近真实分布求解。其中建议分布需要具备以下条件：

采样过程为：

那么随机点必然会出现两种情况：
1）数据点在真实分布曲线（红色）内，那么该点就会被接受；
2）数据点在建议分布曲线（蓝色）内，却不在真实分布曲线内，即灰色部分，那么该点就会被拒绝；
从而出现了一个新的名次——接收率=红色曲线的面积/蓝色曲线的面积。这个概念在一定程度上描述了采样的效率。
接收率的理论值为：
那么，对于高维空间中，M非常大，那么拒绝率就会非常高。

常用的建议分布有：均匀分布、正态分布等。
对于一个复杂的PDF，可以有多个建议分布，只是每个分布的效率并不相同而已。

example 3

注：这里的公式多了一个分母2，其他都是对的
matlab code：

%% 三角分布采样[-1, 1], c=0 均匀分布->建议分布clear; clc;fx = @(x)(x < 0).*(x + 1) + (x >= 0).*(1 - x); % p(x)g = -1:.1:1;y = fx(g);figure(1),clfplot(g, y, 'r-', 'linewidth', 2)% 建议分布q(x) 服从于 uniform(-1, 1)k = 2;y2 = ones(size(g))*0.5*k;hold onplot(g, y2, 'y-', 'linewidth', 2)% sampling pointsn = 10000;xx = zeros(n, 1);yy = zeros(n, 1);i = 1;count = 0;while(1)    if i <= n        xx(i) = rand*2 - 1; % [-1,1]随机数        uu = rand;        yy(i) = k*0.5*uu;        count = count + 1;        if yy(i) <= fx(xx(i))            i = i + 1;                    end    else        break;    endendhold onplot(xx, yy, 'bo')acceptance = n / count;gtext(num2str(acceptance));legend('p(x)', 'q(x)', 'sampling points')

结果：

example 4: 对截断正态分布采样（有待补充 PS：建议分布可以为均匀分布、正态分布和指数分布）

4.重要性采样

当p(x)不太好采样的时候，利用建议分布q(x)来近似积分：

那么积分可以由下列式子近似：

上述式子的积分估计为无偏估计，但是实际应用中建议用带权重的公式（这是一个有偏估计，用很小的偏差来换来方差的减小）代替：

注意：
1)与接受/拒绝采样中类似，这里的建议分布q(x)也是任意的。只是当q(x)与p(x)更接近 并且 q(x)尾部较厚的时候 方差更小，建议分布采样效率更高。（这里不再需要满足π(x)<=M*q(x)）
2)当q(x)与p(x)更接近：w(x)的取值范围会小一些，否则会很大，不利。

重要性采样和接受/拒绝采样都只有建议分布与真实分布近似时才表现很好；
在高维空间中，通常很难找到合适的建议分布，因而上述两种方法将不再奏效。

============分割线================

5.MCMC(Markov chain Monte carlo)

MCMC是一种利用一定范围内的均匀分布的随机数，对高维空间概率进行采样的通用技术。其基本思想：设计一个马尔可夫链，使得其稳定概率为目标分布π(x)
markov chain: 现在只与过去有关，与未来没有关系。相关概念有转移概率、状态空间。
齐次马尔可夫链：
要求状态空间中每个状态都是互通的，不存在吸收态。

稳定的马尔可夫链：
π(n)=π(n-1)P 其中π(0)为任意的初始状态，n=1,2,…,n
经过n次迭代之后，若能够达到π=πP，那么π称为马尔可夫链的稳定状态。
若x = [1, 0, 0, 0, 0];

x(1) = [0.4 0.6 0 0 0];
x(10) = [0.1845646996 0.2055241914 0.13880994 0.267643677 0.203457492]
x(20) = [0.171327920728781 0.205193237057640 0.130988811098497 0.281358951140206 0.211131079974876]
已经基本上不变了，趋于稳定分布。

设计马尔可夫链：只需要计算得到P即可。若状态数目R，概率转移矩阵P，那么已知2R个方程，
1)R个方程：P的行和为1；
2)R个方程：π=πP；
求解P的R^2个未知数。

下面将介绍几种MCMC算法，其区别就在于不同的思路设计马尔可夫链的概率转移矩阵P。

5.1 Metropolis-Hasting algorithm

Metropolis最初提出的概率转移矩阵是对称的，Hasting对其进行了改进。现在广泛应用于高维空间中。
该算法利用必要条件设计概率转移矩阵P：若f满足细致平衡，那么f必定是马尔可夫链的一个平稳分布的，也就是说该马尔可夫链必定是平衡的。
细致平衡的定义：

高维空间中P就不再是二维矩阵的形式，因而通常不再存储该稀疏矩阵。

构建平稳的马尔可夫链步骤：

接收/拒绝操作：若希望提高接收率，那么会希望两者比较对称，使得min{}中左边式子较大。（teacher一直在举例：如果中国与日本做贸易，那么肯定是希望双方都是贸易平衡的，才会愿意继续进行贸易。）

以中心为central，局部均匀移动。重点是选取合适的建议分布q(x)，太宽，会导致拒绝得太多；而太窄也不好，相当于每一个假设都接受了。

5.2 Gibbs sampling

由于我们比较熟悉一维分布采样，Gibbs就是将高维空间采样转化为多个一维空间的采样。

条件分布的形式看着比较复杂，实际上是比较简单，因为真正有影响的是相邻值。因而，与马尔科夫随机场等模型比较接近。