EM算法原理详解与高斯混合模型

借助于machine learning cs229和文章【1】中的内容把EM算法的过程顺一遍，加深一下印象。
关于EM公式的推导，一般会有两个证明，一个是利用Jesen不等式，另一个是将其分解成KL距离和L函数，本质是类似的。

下面介绍Jensen EM的整个推导过程。

1. Jensen不等式

   回顾优化理论中的一些概念。设f是定义域为实数的函数，如果对于所有的实数x，f′′(x)≥0，那么f是凸函数。当x是向量时，如果其hessian矩阵H是半正定的（H≥0），那么f是凸函数。如果f′′(x)>0或者H>0，那么称f是严格凸函数。

   Jensen不等式表述如下：

   如果f是凸函数，X是随机变量，那么
   

   E[f(x)]≥f(E[x])
   
   

   特别地，如果f是严格凸函数，那么

   E[f(x)]>f(E[x])
   当且仅当p(X=E(X))=1，也就是说X是常量。

   这里我们将f(E[X])简写为f(EX)。

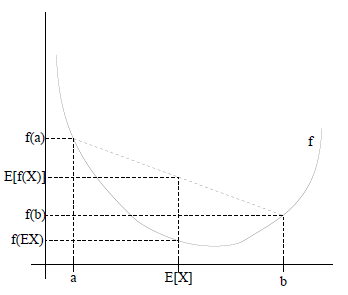
   如果用图表示会很清晰：

   图中，实线f是凸函数，X是随机变量，有0.5的概率是a，有0.5的概率是b。（就像掷硬币一样）。X的期望值就是a和b的中值了，图中可以看到

   E[f(x)]≥f(E[x])
   成立。

   当f是（严格）凹函数当且仅当−f是（严格）凸函数。

   Jensen不等式应用于凹函数时，不等号方向反向，也就是E[f(x)]≤f(E[x])。

---

1. EM算法

   给定的训练样本是{x(1),...,x(m)}，样例间独立，我们想找到每个样例隐含的类别z，能使得p(x,z)最大。p(x,z)的最大似然估计如下：

l(θ)=∑i=1mlog p(x(i);θ)=∑i=1mlog∑zp(x(i),z(i);θ)

第一步是对极大似然取对数，第二步是对每个样例的每个可能类别z求联合分布概率和。但是直接求θ一般比较困难，因为有隐藏变量z存在，但是一般确定了z后，求解就容易了。
EM是一种解决存在隐含变量优化问题的有效方法。既然不能直接最大化l(θ)，我们可以不断地建立l(θ)的下界（E步），然后优化下界（M步）。这句话比较抽象，看下面的。
对于每一个样例i，让Qi表示该样例隐含变量z的某种分布，Qi满足的条件是∑zQi(z)=1,Qi(z)≥1。（如果z是连续性的，那么clip_image032[2]是概率密度函数，需要将求和符号换做积分符号）。比如要将班上学生聚类，假设隐藏变量z是身高，那么就是连续的高斯分布。如果按照隐藏变量是男女，那么就是伯努利分布了。

可以由前面阐述的内容得到下面的公式：

∑i=1mlogp(x;θ)=∑i=1mlog∑z(i)p(x(i),z(i);θ)=∑i=1mlog∑zQi(z(i))p(x(i),z(i);θ)Qi(z(i))≥∑i=1m∑zQi(z(i))logp(x(i),z(i);θ)Qi(z(i))(1)(2)(3)

（1）到（2）比较直接，就是分子分母同乘以一个相等的函数。（2）到（3）利用了Jensen不等式，考虑到log（x）是凹函数（二阶导数小于0），而且

∑zQi(z(i))p(x(i),z(i);θ)Qi(z(i))

就是p(x(i),z(i);θ)Qi(z(i))的期望（回想期望公式中的Lazy Statistician规则）
设Y是随机变量X的函数y=g(x)（g是连续函数），那么
（1） X是离散型随机变量，它的分布律为P(X=xk)=pk,k=1,2,....若∑∞k=1g(xk)pk绝对收敛，则有
E(Y)=E[g(X)]=∑∞k=1g(xk)pk
（2） X是连续型随机变量，它的概率密度为f(x)，若∫∞−∞g(x)f(x)dx绝对收敛，则有
E(Y)=E[g(X)]=∫∞−∞g(x)f(x)dx
对应于上述问题，Y是p(x(i),z(i);θ)Qi(z(i))，X是z(i)，Qi(z(i))是pk，g是z(i)到p(x(i),z(i);θ)Qi(z(i))的映射。这样解释了式子（2）中的期望，再根据凹函数时的Jensen不等式：

f(Ez(i)∼Qi[p(x(i),z(i);θ)Qi(z(i))])≥Ez(i)∼Qi[f(p(x(i),z(i);θ)Qi(z(i)))]

可以得到（3）。
这个过程可以看作是对l(θ)求了下界。对于Qi的选择，有多种可能，那种更好的？假设θ已经给定，那么l(θ)的值就决定于Qi(z(i))和p(x(i),z(i))了。我们可以通过调整这两个概率使下界不断上升，以逼近l(θ)的真实值，那么什么时候算是调整好了呢？当不等式变成等式时，说明我们调整后的概率能够等价于l(θ)了。按照这个思路，我们要找到等式成立的条件。根据Jensen不等式，要想让等式成立，需要让随机变量变成常数值，这里得到：

p(x(i),z(i);θ)Qi(z(i))=c

c为常数，不依赖于z(i)。对此式子做进一步推导，我们知道∑zQi(z(i))=1，那么也就有∑zp(x(i),z(i);θ)=c，（多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是c），那么有下式：

Qi(z(i))=p(x(i),z(i);θ)∑zp(x(i),z(i);θ)=p(x(i),z(i);θ)p(x(i);θ)=p(z(i);x(i)θ)

至此，我们推出了在固定其他参数θ后，Qi(z(i))的计算公式就是后验概率，解决了Qi(z(i))如何选择的问题。这一步就是E步，建立l(θ)的下界。接下来的M步，就是在给定Qi(z(i))后，调整l(θ)，去极大化l(θ)的下界（在固定Qi(z(i))后，下界还可以调整的更大）。那么一般的EM算法的步骤如下：
循环重复直到收敛 {
（E步）对于每一个i，计算

Qi(z(i))=p(z(i);x(i)θ)

（M步）计算

θ=argmaxθ∑i=1m∑zQi(z(i))logp(x(i),z(i);θ)Qi(z(i))

那么究竟怎么确保EM收敛？假定θt和θt+1是EM第t次和t+1次迭代后的结果。如果我们证明了l(θt)≤l(θt+1)，也就是说极大似然估计单调增加，那么最终我们会到达最大似然估计的最大值。下面来证明，选定θ(t)后，我们得到E步
Qi(z(i))=p(z(i);x(i)θ)
这一步保证了在给定θ(t)时，Jensen不等式中的等式成立，也就是

l(θ(t))=∑i=1m∑zQi(z(i))logp(x(i),z(i);θ)Qi(z(i))

然后进行M步，固定Qi(z(i))，并将θ(t)视作变量,由EM的操作可以推导出以下式子成立：

l(θ(t+1))≥∑i=1m∑zQi(z(i))logp(x(i),z(i);θ(t+1))Qi(z(i))≥∑i=1m∑zQi(z(i))logp(x(i),z(i);θ(t))Qi(z(i))=l(θ)(4)(5)(6)

等式（4）成立是由于琴生不等式，等式（5）成立是由于我们在M步取得是max操作。
如果我们定义

J(Q,θ)=∑i=1m∑z(i)Qi(z(i))logp(x(i),z(i);θ)Qi(z(i))

从前面的推导中我们知道l(θ)≥J(Q,θ)，EM可以看作是J的坐标上升法，E步固定θ，优化Q，M步固定Q优化θ。

1. 重新审视混合高斯模型

   我们已经知道了EM的精髓和推导过程，再次审视一下混合高斯模型。之前提到的混合高斯模型的参数Φ和μ，为了简单，这里在M步只给出Φ和μ的推导方法。

E步很简单，按照一般EM公式得到：

w(i)j=Qi(z(i)=j)=P(z(i)=j|x(i);ϕ,μ,Σ)=ϕjp(x(i)|z(i)=j;ϕ,μ,Σ)Σj=1kϕjp(x(i)|z(i)=j;ϕ,μ,Σ)

简单解释就是每个样例i的隐含类别z(i)为j的概率可以通过后验概率计算得到。ϕ是每个类的概率。
在M步中，我们需要在固定Qi(z(i))后最大化最大似然估计，也就是

==∑i=1m∑z(i)Qi(z(i))logp(x(i),z(i);ϕ,μ,Σ)Qi(z(i))∑i=1m∑j=1kQi(z(i)=j)logp(x(i)|z(i)=j;ϕ,μ,Σ)p(z(i)=j;ϕ)Qi(z(i))∑i=1m∑j=1kw(i)jlog1(2π)n/2|Σj|1/2exp(−12(x(i)−μj)TΣ−1j(x(i)−μj)).ϕjw(i)j

这是将z(i)的k种情况展开后的样子，未知参数ϕj,μj和Σj。
固定ϕj,和Σj，对μj求导得

===∇μj∑i=1m∑z(i)Qi(z(i))logp(x(i),z(i);ϕ,μ,Σ)Qi(z(i))−∇μj∑i=1m∑j=1kw(i)j12(x(i)−μj)TΣ−1j(x(i)−μj))12∑i=1mw(i)j∇μj(2μTjΣ−1jx(i)−μTjΣ−1μj)∑i=1mw(i)j(Σ−1jx(i)−Σ−1μj)

等于0时，得到
μj=∑mi=1w(i)jx(i)Σmi=1w(i)j
这就是我们之前模型中的μ的更新公式。
然后推导ϕ的更新公式。看之前得到的

∑i=1m∑j=1kw(i)jlog1(2π)n/2|Σj|1/2exp(−12(x(i)−μj)TΣ−1j(x(i)−μj)).ϕjw(i)j

分子和分母上与ϕ无关的常数都可以通过log提取出来，，实际上需要优化的公式是：

∑i=1m∑j=1kw(i)jlogϕj

需要知道的是，ϕj还需要满足一定的约束条件就是Σkj=1ϕj=1。
这个优化问题我们很熟悉了，直接构造拉格朗日乘子。

L(ϕ)=∑i=1m∑j=1kw(i)jlogϕj+β(∑j=1kϕj−1)

还有一点就是ϕj>0，但这一点会在得到的公式里自动满足。
求导得，
∂∂ϕjL(ϕ)=∑mi=1w(i)jϕj+β
等于0，得到
ϕj=∑mi=1w(i)j−β
也就是说ϕj∝∑mi=1w(i)j再次使用∑kj=1ϕj=1，得到
−β=∑mi=1∑kj=1w(i)j=Σmi=11=m
这样就神奇地得到了β。
那么就顺势得到M步中ϕj的更新公式：
ϕj=1m∑mi=1w(i)j
Σ的推导也类似，不过稍微复杂一些，毕竟是矩阵。结果在之前的混合高斯模型中已经给出。

Σ=∑mi=1w(i)j(x(i)−μj)(x(i)−μj)T∑mi=1w(i)j

关于EM证明的补充，一般情况下可以通过Jensen不等式得到∑mi=1logp(x;θ)的下界来求解，但是将该公式展开似乎更直观一些。
首先是将p(x;θ)拆分开来，我们注意到p(x,z;θ)=p(x;θ)p(z|x;θ)这里有联合概率，x的生成概率，z的后验概率，取log然后做一下变换

lnp(x;θ)=lnp(x,z;θ)−lnp(z|x;θ）=lnp(x,z;θ)−lnq(z)−[lnp(z|x;θ)−lnq(z)]=lnp(x,z;θ)q(z)−lnlnp(z|x;θ)q(z)

同时乘以q(z)并对q(z)求和得到

Σzq(z)lnp(x;θ)=Σz[q(z)(lnp(x,z;θ)q(z)−lnlnp(z|x;θ)q(z))]

由于z与p(x;θ)独立，并且σz(q)=1,所以又

lnp(x;θ)=Σzq(z)np(x,z;θ)q(z)−Σzq(z)lnlnp(z|x;θ)q(z)

写作

lnp(x;θ)=L(q;θ)+KL(q||p)

看到这里应该很明白了，在NG的推导中放缩掉的是这里的KL距离，最后得到的是这里的L(q;θ),当q(z)和p(z;x,θ)相等时KL距离为0，前面的推导的等式成立。

E-step
假设当前的参数为θold,则Estep可以被描述为：固定θold找一个分布q(z),使得L(q,θold)最大
由于lnp(x;θold与z无关则使L(q,θold)最大姐使KL(q||p)最小（=0），也就是说q(z)=p(z;x,θold)

回想高斯混合分布，用p(z;x,μ,σ,π)去求E[z]，这个时候KL（q||p）=0
M-step：固定q(z)找一组参数θnew,使得L(q,θnew)最大，
lnp(x;θ)的增大可能来自两部分L(q,θnew)和KL(q||p)（因为此时p(z;x,θnew)）而q(z;x,θold),p≠q

这里可以看到，L的下届提高了，ln(p(x;θ)的下届也提高了。

参考：
【1】
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html#2831962
【2】http://wenku.baidu.com/view/d5e6973a87c24028915fc361.html
【3】http://cs229.stanford.edu/materials.html
【4】http://freemind.pluskid.org/machine-learning/regularized-gaussian-covariance-estimation/