[BZOJ 3295] CQOI 2011 动态逆序对 · 分块 & 逆序对
来源:互联网 发布:淘宝开茶叶店 编辑:程序博客网 时间:2024/05/17 08:55
最优算法CDQ分治或树套树,并不会做。
分块大法好!
要求每次删除前的逆序对数,可以转化成求每次删除一个数后的逆序对数。
删除之前的对数,减去与当前要删除的数相关的逆序对数,就是每次的答案。
我们可以把原序列a[]分成个块,每个块有
个数。然后维护一个b[],b[]中的每一个块都是一个单调递增的序列。
当前要删除的数为x,所在的块是k,那我们分两种情况做:
1.对于k号块,直接在a[]的k号块中枚举求逆序对,复杂度为。
2.对于除了k号块以外的每一个块,利用b[]二分求x在当前块中产生的逆序对数,复杂度为。
然后删除这个数,把b[]中相对应的数变为0,把这个块重新排序。
因为我们要保证每个块的大小不变,并且每个数所在的块的编号也不变,所以我们在删除的时候不能直接删除。
既然不能直接删除,我们就得搞一些东西来维护。
在计算第一步的时候,我们开一个bool数组f[i],表示i这个数有没有被删掉,然后枚举的时候判断一下。
在计算第二步的时候,我们开一个数组sum[],sum[i]表示第i个块里删除了多少个数。这样的话,如果我们在计算的时候这个块里产生了t对逆序对,而已经被删除的数都变成0,所以每个0都会产生一个逆序对,那么不算上已经被删除的实际只有t-sum[i]个逆序对。
具体细节见注释。
#include <cstdio>#include <cmath>#include <cstdlib>#include <algorithm>#include <cstring>using namespace std;#define ll long long const int N=200050;int n,m,a[N];int tmp[N],t[N];//merge-sortint belong[N],L[N],R[N],cnt,k,x,y;int ad[N]; //i在原数列中的位置为ad[i] int b[N]; //每个块维护有序数列 int sum[N]; //当前块中删除了多少个数 int adx;int i;bool f[N];ll tot; //当前逆序对数 开 long long ! inline int get(){ int p=0;char x=getchar(); while (x<'0' || x>'9') x=getchar(); while (x>='0' && x<='9') p=p*10+x-'0',x=getchar(); return p; } inline void merge_sort(int l,int r){ int mid,p,i,j; mid=(l+r)>>1; i=p=l;j=mid+1; while (i<=mid && j<=r) if (tmp[i]>tmp[j]) t[p++]=tmp[j++],tot+=mid-i+1; else t[p++]=tmp[i++]; while (i<=mid) t[p++]=tmp[i++]; while (j<=r) t[p++]=tmp[j++]; for (i=l;i<=r;i++) tmp[i]=t[i]; return ;} inline void merge(int l,int r){ if (l>=r) return ; int mid=(l+r)>>1; merge(l,mid); merge(mid+1,r); merge_sort(l,r); return ;} void init(){ n=get();m=get(); k=sqrt(n); //块大小 cnt=n/k;if (n%k) cnt++; //块个数 for (int i=1;i<=n;i++) a[i]=get(),ad[a[i]]=i,belong[i]=(i-1)/k+1; for (int i=1;i<=cnt;i++) L[i]=i*k-k+1,R[i]=i*k; R[cnt]=n; memcpy(tmp,a,sizeof tmp); tot=0; merge(1,n); memcpy(b,a,sizeof a); for (int i=1;i<=cnt;i++) sort(b+L[i],b+R[i]+1); memset(f,1,sizeof f); return ;} inline int search(int t,int p){ int l,r,ret; l=L[t]; r=R[t]; ret=R[t]; while (l<=r){ int mid=(l+r)>>1; if (b[mid]<=p) ret=mid,l=mid+1; else r=mid-1; } if (b[ret]>p) ret=L[i]-1; return ret;} int main(){ init(); for (int p=1;p<=m;p++){ printf("%lld\n",tot); y=get();x=ad[y]; //得到在a数列中的位置 所处的块的编号肯定不变 k=belong[x]; //x属于第k个块 for (i=1;i<k;i++) tot-=R[i]-search(i,a[x]); for (i=k+1;i<=cnt;i++) tot-=search(i,a[x])-L[i]+1-sum[i]; for (i=L[k];i<x;i++) if (f[a[i]] && a[i]>a[x]) tot--; for (i=x+1;i<=R[k];i++) if (f[a[i]] && a[i]<a[x]) tot--; adx=search(k,a[x]);b[adx]=0;sum[k]++;f[a[x]]=0; sort(b+L[k],b+R[k]+1); } return 0;}2.对于k号块,直接在a[]的k号块中枚举求逆序对,复杂度为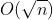
0 0
- [BZOJ 3295] CQOI 2011 动态逆序对 · 分块 & 逆序对
- BZOJ 3295 CQOI 2011 动态逆序对 线段树套Treap
- 【BZOJ 3295】动态逆序对 - 分块+树状数组
- BZOJ 3295: [Cqoi2011]动态逆序对 分块大法好
- BZOJ 3295 动态逆序对
- [BZOJ 3295]动态逆序对
- BZOJ 3295 动态逆序对 CDQ分治
- [BZOJ 3295] Cqoi2011 动态逆序对
- 【BZOJ 3295】 [Cqoi2011]动态逆序对
- BZOJ 3295 [Cqoi2011]动态逆序对
- BZOJ 3295 [CQOI2011] 动态逆序对
- BZOJ 3295: [Cqoi2011]动态逆序对
- 【BZOJ 3295】[Cqoi2011]动态逆序对
- bzoj 3295 动态逆序对 CDQ分治
- bzoj 3295 [Cqoi2011]动态逆序对
- BZOJ 3295 动态逆序对 CDQ分治
- BZOJ 3295 [Cqoi2011]动态逆序对
- [BZOJ]P3295-动态逆序对
- 第一题
- P,V操作的历史背景:信号量机制???
- 第二题
- C++两个队列实现一个栈
- 欢迎使用CSDN-markdown编辑器
- [BZOJ 3295] CQOI 2011 动态逆序对 · 分块 & 逆序对
- 在myeclipse10中安装jad反编译工具
- html5中的问题总结
- 黑马程序员---2015.6.21.java基础笔记---TreeSet---HashSet---HashMap
- DML-数据更新
- struts 2 上传文件的位置
- POJ 1502 MPI Maelstrom (简单最短路,多种算法均可)
- java基础—IO流——转换流的操作
- 轻松搞定面试中的二叉树题目


