hdu5301-multi-university contest 2 -1002

链接：http://acm.hdu.edu.cn/showproblem.php?pid=5301

欢迎参加——BestCoder周年纪念赛（高质量题目+多重奖励）

Buildings

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 923    Accepted Submission(s): 267

Problem Description

Your current task is to make a ground plan for a residential building located in HZXJHS. So you must determine a way to split the floor building with walls to make apartments in the shape of a rectangle. Each built wall must be paralled to the building's sides.

The floor is represented in the ground plan as a large rectangle with dimensions n×m, where each apartment is a smaller rectangle with dimensions a×b located inside. For each apartment, its dimensions can be different from each other. The numbera and b must be integers.

Additionally, the apartments must completely cover the floor without one 1×1 square located on (x,y). The apartments must not intersect, but they can touch.

For this example, this is a sample of n=2,m=3,x=2,y=2.



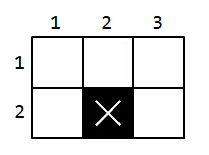
To prevent darkness indoors, the apartments must have windows. Therefore, each apartment must share its at least one side with the edge of the rectangle representing the floor so it is possible to place a window.

Your boss XXY wants to minimize the maximum areas of all apartments, now it's your turn to tell him the answer.

 

Input

There are at most 10000 testcases.
For each testcase, only four space-separated integers, n,m,x,y(1≤n,m≤108,n×m>1,1≤x≤n,1≤y≤m).

 

Output

For each testcase, print only one interger, representing the answer.

 

Sample Input

2 3 2 23 3 1 1

 

Sample Output

12
Hint
Case 1 :You can split the floor into five 1×1 apartments. The answer is 1.Case 2:You can split the floor into three 2×1 apartments and two 1×1 apartments. The answer is 2.If you want to split the floor into eight 1×1 apartments, it will be unacceptable because the apartment located on (2,2) can't have windows.

//题意是求  用矩形来填充大矩形，保证每个小矩形可以与大矩形的边相连//当m==n且x==y且2*x-1==m时(即为正方形且边长为奇数)且黑色方块在中心上）//00000//00000//00x00//00000//00000      答案为m/2//当m<n或者m>n都转化为 m>n//000000000000000//000x00000000000//000000000000000//000000000000000     ans=(n+1)/2,len1=max(x-1,n-x),len2=min(y,m-y+1)//                                       答案即为max(min(len1,len2),ans)#include <iostream>#include "stdio.h"#include "stdlib.h"#include "string.h"#include "math.h"#include <algorithm>using namespace std;int main(){    int n,m,x,y;    while(scanf("%d%d%d%d",&n,&m,&x,&y)!=EOF)    {        if(n==m&&x==y&&2*x-1==n) {printf("%d\n",n/2);  continue; }        if(n>m) {            swap(n,m);swap(x,y);        }        int ans=(n+1)/2,len1=max(x-1,n-x),len2=min(y,m-y+1);        ans=max(min(len1,len2),ans);        printf("%d\n",ans);    }    return 0;}