杭电1022 Train Problem I

Train Problem I

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 25879    Accepted Submission(s): 9771

Problem Description

As the new term comes, the Ignatius Train Station is very busy nowadays. A lot of student want to get back to school by train(because the trains in the Ignatius Train Station is the fastest all over the world ^v^). But here comes a problem, there is only one railway where all the trains stop. So all the trains come in from one side and get out from the other side. For this problem, if train A gets into the railway first, and then train B gets into the railway before train A leaves, train A can't leave until train B leaves. The pictures below figure out the problem. Now the problem for you is, there are at most 9 trains in the station, all the trains has an ID(numbered from 1 to n), the trains get into the railway in an order O1, your task is to determine whether the trains can get out in an order O2.

 

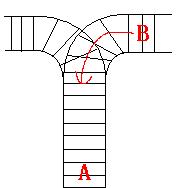
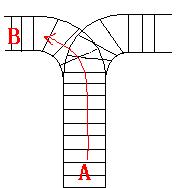
Input

The input contains several test cases. Each test case consists of an integer, the number of trains, and two strings, the order of the trains come in:O1, and the order of the trains leave:O2. The input is terminated by the end of file. More details in the Sample Input.

 

Output

The output contains a string "No." if you can't exchange O2 to O1, or you should output a line contains "Yes.", and then output your way in exchanging the order(you should output "in" for a train getting into the railway, and "out" for a train getting out of the railway). Print a line contains "FINISH" after each test case. More details in the Sample Output.

 

Sample Input

3 123 3213 123 312

 

Sample Output

Yes.inininoutoutoutFINISHNo.FINISH
Hint
Hint
 For the first Sample Input, we let train 1 get in, then train 2 and train 3.So now train 3 is at the top of the railway, so train 3 can leave first, then train 2 and train 1.In the second Sample input, we should let train 3 leave first, so we have to let train 1 get in, then train 2 and train 3.Now we can let train 3 leave.But after that we can't let train 1 leave before train 2, because train 2 is at the top of the railway at the moment.So we output "No.".

 

题目大意：

        一个火车中转站最多可以停放9辆火车，其车辆进站出站符合先进后出原则，给定进站和出站两个字符串，判断其是不是符合题意，如果符合的话输出其过程。

解题思路

        很明显这是一道可以利用栈解答的题目，因为栈的特性也是先进后出，建立两个字符数组存储给定的两个字符串，然后建立一个栈，建立一个数组存储其操作过程，分别定义指向第一个字符串、第二个字符串、操作过程的指针，然后开始循环操作：如果栈空则进栈，字符串A指针+1；如果不空则栈顶元素跟字符串B[字符串B指针]比较，同则出栈且字符串B指针+1，否则字符串A[字符串A指针]入栈且字符串A指针+1，直到字符串B指针跟字符串B长度相等。其中利用过程数组脚码来标记每次操作，进栈则为1，出栈则为0。

#include<stdio.h>#define max 20char in[max],out[max],target[max],stack[max];//进入顺序 步骤 目标顺序 栈 当前在车站里的火车int main(){int n,top,nowpos,head,step;//top栈顶  nowpos达成目标进度  head车队头 step 步骤数 while(~scanf("%d",&n)){scanf("%s %s",in,target);top=nowpos=head=step=0;while(head<n){stack[++top]=in[head++];//stack[1]=int[0]先把车一个个进栈 out[step++]='1';//步骤进去为1出去为0 while(top&&stack[top]==target[nowpos])//循环直到车一个个进栈，最后一辆车的编号和出去第一辆车编号相同进入循环 {top--;//出去一辆栈顶-1 nowpos++;//完成进度加1 out[step++]='0';//出去的步骤加1； }}if(nowpos==n)//如果完成的进度数等于n则可以完成过程 {printf("Yes.\n");for(int i=0;i<step;i++){if(out[i]=='0')printf("out\n");elseprintf("in\n");}printf("FINISH\n");}elseprintf("No.\nFINISH\n");}return 0;}