整数拆分问题(从O(n^2优化到O(n*sqrt(n))

　1. 将n划分成若干正整数之和的划分数。
　　2. 将n划分成k个正整数之和的划分数。
　　3. 将n划分成最大数不超过k的划分数。
　　4. 将n划分成若干奇正整数之和的划分数。
　　5. 将n划分成若干不同整数之和的划分数。

1.将n划分成不大于m的划分法：
　　1).若是划分多个整数可以存在相同的：
　　 dp[n][m]= dp[n][m-1]+ dp[n-m][m] dp[n][m]表示整数 n 的划分中，每个数不大于 m 的划分数。
　　则划分数可以分为两种情况:
　　a.划分中每个数都小于 m，相当于每个数不大于 m- 1, 故划分数为 dp[n][m-1].
　　 b.划分中有一个数为 m. 那就在 n中减去 m ,剩下的就相当于把 n-m 进行划分， 故划分数为 dp[n-m][m];
　　2).若是划分多个不同的整数：
　　dp[n][m]= dp[n][m-1]+ dp[n-m][m-1] dp[n][m]表示整数 n 的划分中，每个数不大于 m 的划分数。
　　 同样划分情况分为两种情况：
　　a.划分中每个数都小于m,相当于每个数不大于 m-1,划分数为 dp[n][m-1].
　　b.划分中有一个数为 m.在n中减去m,剩下相当对n-m进行划分，
　　　并且每一个数不大于m-1，故划分数为 dp[n-m][m-1]
　　2.将n划分成k个数的划分法：
　　　　dp[n][k]= dp[n-k][k]+ dp[n-1][k-1];
　　方法可以分为两类：
　　　　第一类: n 份中不包含 1 的分法，为保证每份都 >= 2，可以先拿出 k 个 1 分
　　到每一份，然后再把剩下的 n- k 分成 k 份即可，分法有: dp[n-k][k]
　　 　　第二类: n 份中至少有一份为 1 的分法，可以先那出一个 1 作为单独的1份，剩
　　下的 n- 1 再分成 k- 1 份即可，分法有：dp[n-1][k-1]
　　
　　3.将n划分成若干奇数的划分法：（不懂）
　　　　g[i][j]:将i划分为j个偶数
　　　　f[i][j]:将i划分为j个奇数
　　 g[i][j] = f[i - j][j];
　　f[i][j] = f[i - 1][j - 1] + g[i - j][j];

以下给出O(n^2)算法

/*对于输入的 n,k; 第一行： 将n划分成若干正整数之和的划分数。 第二行： 将n划分成k个正整数之和的划分数。 第三行： 将n划分成最大数不超过k的划分数。 第四行： 将n划分成若干个 奇正整数之和的划分数。 第五行： 将n划分成若干不同整数之和的划分数。 第六行： 打印一个空行*/  #include<iostream>  #include <cstring>  #include<vector>  #include <cstdio>  using namespace std;  #define N 55+1  int dp[N][N];  int main()  {      //分为若干个正整数和      //memset(dp,0,sizeof(dp));      int n,k;      int out[6];      while(cin>>n>>k)      {          memset(dp,0,sizeof(dp));          //任意个正整数和，则dp[i][j]表示i分解成最大不超过j的个数，          //分为最大是j和最大不是j，则dp[i][j]=dp[i-j][j]+dp[i][j-1];          dp[0][0]=1;          for (int i=0;i<=n;i++)          {              for (int j=1;j<=n;j++)              {                  if(j<=i)                  dp[i][j]=dp[i-j][j]+dp[i][j-1];                  else                  dp[i][j]=dp[i][i];              }          }          out[1]=dp[n][n];          out[3]=dp[n][k];          //分成K个正整数的和 ,分为k个数中没有1，和有1，          //dp[i][j],将i划分为j个dp[i][j]=dp[i-j][j]+dp[i-1][j-1];          memset(dp,0,sizeof(dp));          for(int i=1;i<=n;i++)          for (int j=1;j<=i;j++)          {                if(j==1)                dp[i][j]=1;                else                dp[i][j]=dp[i-j][j]+dp[i-1][j-1];           }          out[2]=dp[n][k];         //奇数和dp[i][j]为划分最大的奇数不超过j的数，         //则dp[i][j]=dp[i-n(j)][j]+dp[i][j-2];n(j)为不超过j的最大奇数         //初始条件，dp[i][1]=1,j为偶数时候dp[i][j]=dp[i][j-1];当i==n(j) ,         //出现dp[0][j]，也就是当i为奇数时候，dp[0][j]=1;         memset(dp,0,sizeof(dp));         for(int i=0;i<=n;i++)         {             dp[i][1]=1;             if(i&1)             dp[0][i]=1;          }          for (int i=1;i<=n;i++)          {              for (int j=1;j<=n;j++)              {                  if(j&1)                  {                      if(j<=i)                      dp[i][j]=dp[i-j][j]+dp[i][j-1];                      else                       dp[i][j]=dp[i][i];                  }                  else                  dp[i][j]=dp[i][j-1];              }          }          out[4]=dp[n][n];  //不同正整数和，dp[i][j]是不超过j的不同的整数和，dp[i][j]=dp[i-j][j-1]+dp[i][j-1];初始状态dp[1][1]=1;  //当i==j时，出现dp[0][j-1],表示先拿出一个j出来，这时候就应该是1中情况。          memset(dp,0,sizeof(dp));          dp[0][0]=1;          for (int i=0;i<=n;i++)          {                for (int j=1;j<=n;j++)                {                     if(j<=i)                     dp[i][j]=dp[i-j][j-1]+dp[i][j-1];                      else                      dp[i][j]=dp[i][i];                }          }          out[5]=dp[n][n];          for (int i=1;i<=5;i++)              {                  cout<<out[i]<<endl;              }              cout<<endl;         }  }     

但我在做51nod的时候发现数据给的范围很大(5*10^4)，这种方法不仅内存存不下，而且还TLE

下面给出n个数拆成不同数的方案的O(nsqrt(n))算法

dp[i][j]代表i个数相加等于j
由于有不同的数最多不超过O(sqrt(n))算法个，则可以优化

dp[i][j] = dp[i-1][j-i] + dp[i][j-i]

这个递推方程的转移含义是i-1个数每个数都加1,最后再添上一个1，就从dp[i-1][j-i]转到dp[i][j],还有就是i个数每个数都加1，就从dp[i][j-i]转到dp[i][j]

#include <iostream>#include <cstdio>#include <algorithm>#include <string>#include <cmath>int dp[600][51000];int const mod = 1e9+7;using namespace std;int main(){  int n;  while(scanf("%d",&n) != EOF){     dp[0][0] = 1;      for(int i =1; i <= 2*(int)sqrt(n); i++ )      {          for(int j = 0; j <= n; j++)          {              dp[i][j] = (dp[i-1][j-i] + dp[i][j-i])%mod;          }      }      int ans = 0;      for(int i =1; i <= 2*(int)sqrt(n); i++ )      {          ans += dp[i][n];          ans %= mod;      }          printf("%d\n",ans);  }  return 0;}

那么当将n划分成若干正整数之和的划分数呢？
可以相同，那么上面那个方法就不行了
可以用5边形数来求
参考资料
https://en.wikipedia.org/wiki/Partition_(number_theory)

用一个公式就行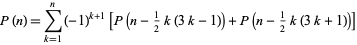

其中n-k*(3*k-1)/2>=0,n-k*(3*k+1)/2>=0；
注意两个条件要分开判断，有大于0的就加上相应的f，不是两个同时成立或者不成立

这个公式的时间复杂度是O(n^1.5)

#include <iostream>#include <cstring>#include <cmath>using namespace std;long long tar[100002];const int MOD=1000000007;void init(){    memset(tar,0,sizeof(tar));    tar[0]=1;    for(int i=1;i<=50000;i++)    {        int nbit;        for(int j=1;;j++)        {            int element1,element2;            element1=i-j*(3*j-1)/2;            element2=i-j*(3*j+1)/2;            if(j&1)                nbit=1;            else if(j%2==0)                nbit=-1;            if(element2<0 && element1<0)                break;            if(element1>=0)            {                tar[i]=(tar[i]+nbit*tar[element1])%MOD;            }            if(element2>=0)            {                tar[i]=(tar[i]+nbit*tar[element2])%MOD;            }        }        tar[i]=(tar[i]+MOD)%MOD;    }}int main(){    init();    int rat;    while(cin>>rat)    {        cout<<tar[rat]<<endl;    }    return 0;}

计算机是人造学科，数学是神造学科！！！orz….