HDU 5434 Peace small elephant
来源:互联网 发布:从来不想谈恋爱 知乎 编辑:程序博客网 时间:2024/06/15 02:07
Problem Description
Xiao Ming likes playing the international chess ,especially like the elephant(it can move by slant while no barrier),
but he think the big elephant of the chess is cruel,and a kind of small elephant is not as cruel as the big elephant.
Its attack range is checks on the ramp of the small elephant's check's right angle.Now Ming is going to put many small elephants on his chessboard.
It's interesting that when two small elephants have a common side they'll become one solidarity elephant,
and more than 2 small elephants also can do this if satisfy the condition,and the attack range of solidarity elephants is same as the small elephant.
Now there is a requirement that it's empty on anyone of elephants' attack range(no piece).Xiao Ming has a special chessboard withm∗n checks.
Please figure out the number of all the plans that satisfy the condition.As the number is too big,we need to have a modulo1000000007 .
The following is pictures show the attack range of elephants with different shape,"X"means attack range.
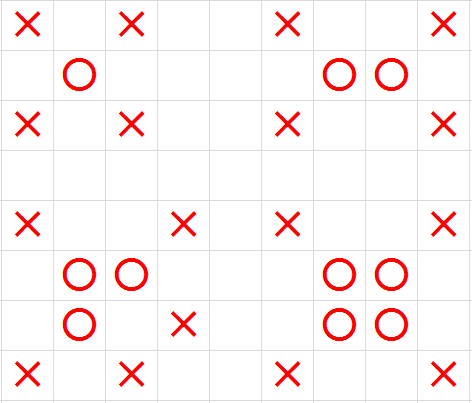
but he think the big elephant of the chess is cruel,and a kind of small elephant is not as cruel as the big elephant.
Its attack range is checks on the ramp of the small elephant's check's right angle.Now Ming is going to put many small elephants on his chessboard.
It's interesting that when two small elephants have a common side they'll become one solidarity elephant,
and more than 2 small elephants also can do this if satisfy the condition,and the attack range of solidarity elephants is same as the small elephant.
Now there is a requirement that it's empty on anyone of elephants' attack range(no piece).Xiao Ming has a special chessboard with
Please figure out the number of all the plans that satisfy the condition.As the number is too big,we need to have a modulo
The following is pictures show the attack range of elephants with different shape,"X"means attack range.

Input
There are at most 5 testcases .
For each testcase contains two integersn,m ,meaning as in the title.
1≤n≤1000000000,1≤m≤7
For each testcase contains two integers
Output
For each testcase print a single integer - the number of all the plans that satisfy the condition.
Sample Input
1 12 3
Sample Output
250递推出矩阵,然后快速幂#include<map>#include<cmath>#include<queue>#include<stack>#include<string>#include<cstdio>#include<vector>#include<cstring>#include<iostream>#include<algorithm>using namespace std;typedef long long LL;const int maxn = 1000000007;LL T, n, m, a[128][128], b[128], ans;bool check(int x, int y){ for (int i = 0; i < n; i++) { int k = 1 << i; if (x&k) { if (y&k) continue; if ((y >> 1)&k) { if (!((x >> 1)&k)) return false; } if ((y << 1)&k) { if (!((x << 1)&k)) return false; } } } return true;}void update(){ LL c[128][128] = { 0 }; for (int i = 0; i < (1 << n); i++) for (int j = 0; j < (1 << n); j++) for (int k = 0; k < (1 << n); k++) (c[i][k] += a[i][j] * a[j][k]) %= maxn; for (int i = 0; i < (1 << n); i++) for (int j = 0; j < (1 << n); j++) a[i][j] = c[i][j];}void get(){ LL c[128] = { 0 }; for (int j = 0; j < (1 << n); j++) for (int k = 0; k < (1 << n); k++) (c[k] += b[j] * a[j][k]) %= maxn; for (int i = 0; i < (1 << n); i++) b[i] = c[i];}int main(){ //scanf("%I64d", &T); //while (T--) while (scanf("%I64d%I64d", &m, &n) != EOF) { for (int i = 0; i < (1 << n); i++) for (int j = 0; j < (1 << n); j++) if (check(i, j)) a[i][j] = 1; else a[i][j] = 0; for (int i = 0; i < (1 << n); i++) b[i] = 1; for (int i = m - 1; i; i >>= 1) { if (i & 1) get(); update(); } ans = 0; for (int i = 0; i < (1 << n); i++) (ans += b[i]) %= maxn; printf("%I64d\n", ans); } return 0;}
0 0
- hdu-5434 Peace small elephant
- HDU 5434 Peace small elephant
- hdu 5434 Peace small elephant
- hdu 5434 Peace small elephant 状压 快速幂
- hdu 5435 Peace small elephant(矩阵快速幂)
- 【矩阵快速幂】 HDOJ 5434 Peace small elephant
- DFS矩阵构造+快速矩阵幂 hdu5434 Peace small elephant
- peace
- peace
- Elephant
- hdu 5980 Find Small A
- HDU 5980 Find Small A
- Hdu-5980-Find Small A
- HDU 5980 Find Small A
- HDU 5980 Find Small A
- hdu 5980 Find Small A
- hdu-5980-Find Small A
- Inner Peace
- 【js】JavaScript中同名标识符优先级
- HDU 5433 Xiao Ming climbing
- Java web实现定时器任务
- eclipse插件
- C++Primer第五版 9.1节练习
- HDU 5434 Peace small elephant
- JAVA一个超级简单的计算器
- input 文本框控制文本输入长度
- Swift第二课 数组与字典
- 各种编程语言的深度学习库收集整理
- 基于OpenSSL自建CA和颁发SSL证书
- 无法注册Parallels Desktop
- Undefined symbols for architecture i386
- Linux下部署web项目


