【Codeforces Round 334 (Div 2)D】【数论 置换群 典型数据特判 附带打表代码】Moodular Arithmetic 满足f(k x)=k f(x)的映射个数

D. Moodular Arithmetic

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

As behooves any intelligent schoolboy, Kevin Sun is studying psycowlogy, cowculus, and cryptcowgraphy at the Bovinia State University (BGU) under Farmer Ivan. During his Mathematics of Olympiads (MoO) class, Kevin was confronted with a weird functional equation and needs your help. For two fixed integers k and p, where p is an odd prime number, the functional equation states that

for some function 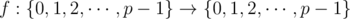. (This equation should hold for any integer x in the range 0 top - 1, inclusive.)

It turns out that f can actually be many different functions. Instead of finding a solution, Kevin wants you to count the number of distinct functions f that satisfy this equation. Since the answer may be very large, you should print your result modulo 10⁹ + 7.

Input

The input consists of two space-separated integers p and k (3 ≤ p ≤ 1 000 000, 0 ≤ k ≤ p - 1) on a single line. It is guaranteed that p is an odd prime number.

Output

Print a single integer, the number of distinct functions f modulo 10⁹ + 7.

Examples

input

3 2

output

3

input

5 4

output

25

#include<stdio.h>#include<iostream>#include<string.h>#include<string>#include<ctype.h>#include<math.h>#include<set>#include<map>#include<vector>#include<queue>#include<bitset>#include<algorithm>#include<time.h>using namespace std;void fre(){freopen("c://test//input.in","r",stdin);freopen("c://test//output.out","w",stdout);}#define MS(x,y) memset(x,y,sizeof(x))#define MC(x,y) memcpy(x,y,sizeof(x))#define MP(x,y) make_pair(x,y)#define ls o<<1#define rs o<<1|1typedef long long LL;typedef unsigned long long UL;typedef unsigned int UI;template <class T1,class T2>inline void gmax(T1 &a,T2 b){if(b>a)a=b;}template <class T1,class T2>inline void gmin(T1 &a,T2 b){if(b<a)a=b;}const int N=1e6+10,M=0,Z=1e9+7,ms63=1061109567;LL p,k;bool e[N];int a[12];int Ans;void dfs(int pos){if(pos==p){bool flag=1;for(int i=0;i<p;++i){if(a[i]*k%p!=a[i*k%p]){flag=0;break;}}if(flag)++Ans;return;}for(int i=0;i<p;++i){a[pos]=i;dfs(pos+1);}}void table(){Ans=0;dfs(0);printf("%d\n",Ans);}int main(){while(~scanf("%lld%lld",&p,&k)){LL ans=1;if(k==0)for(int i=1;i<p;++i)ans=ans*p%Z;else if(k==1)for(int i=0;i<p;++i)ans=ans*p%Z;else{//Way1/*MS(e,0);for(LL i=1;i<p;++i)if(e[i]==0){ans=ans*p%Z;for(LL j=i;e[j]==0;j=j*k%p)e[j]=1;}*///Way2int step=1;for(LL K=k;K!=1;K=K*k%p,++step);step=(p-1)/step;while(step--)ans=ans*p%Z;}printf("%lld\n",ans);//table();}return 0;}/*【trick&&吐槽】这道题一开始就想到，大概答案就是p^(置换群的数量)?写了一发，然而WA掉了TwT，然后写了个对拍找出了问题就AC了。对于这种猜想性比较强的问题，打表又好写，打个表找规律果然是一个绝佳的好办法呀！【题意】让你求出一个映射关系f(x)=y。x和y的取值范围都是[0,p-1]对于每个x，都要满足f[kx%p]==k*f[x]%p恒成立。其中，p是[3,1e6]范围的数，k是[0,p-1]范围的数。数据保证，p为奇数素数。【类型】数论 打表【分析】展开思考过程——首先，k的范围是0base，于是我们一定要好好思考一些特殊数据所对应的情况。1，k==0时，要满足f[0*x]=0*f[x]。我们发现这时必然要满足f[0]=0，其他点都无所谓。所以答案是(p-1)^p2，k==1时，显然f[1*x]=1*f[1]。我们发现这个显然是成立的。所以答案是p^p3，其他情况下，我们找到所有置换群。答案是p^(置换群个数)置换群的个数怎么求呢？方法1——while循环方法2——求循环群大小我们可以设f(x)=v，那么——f(x*k^1%p)=v*k^1*%pf(x*k^2%p)=v*k^2%pf(x*k^3%p)=v*k^3%pf(x*k^4%p)=v*k^4%p我们令m为最小的整数，使得f(x*k^m%p)=v*k^m%p那么显然，对于每个置换群，恰好包含m个数，走过m步后又会回到自己。m也就是循环群大小于是总的置换群的个数=(p-1)/循环群大小。而且，这样写完之后，我们会发现，这个环走过m步后，恰好自变量和因变量都变成了初始值。于是就不会出现前后矛盾的情况。所以这道题就可以顺利AC啦！【时间复杂度&&优化】O(n)*/