PCA原理以及为何要使用协方差矩阵
来源:互联网 发布:seo公司 编辑:程序博客网 时间:2024/05/17 02:22
一、数理统计公式
均值:
 表示样本的平均特征。但是无法表示样本之间的差异,所以就有了。
表示样本的平均特征。但是无法表示样本之间的差异,所以就有了。
方差:
 以及
以及
标准差:

协方差用于表示两个样本参数之间的相似度
协方差:

。从公式上来看,协方差的结果是先求"参数x”与"参数x的均值"之间的之间的差,以及"参数y"和"参数y的均值"之间的差,表达了两个参数xy之间的差异程度。
协方差矩阵:若观测的一个系统有3个参数xyz,而协方差只能计算两个参数之间的差异程度,可以用协方差矩阵来表达参数两两之间的差异程度。

二、PCA原理
PCA是主成分分析。例如对于一个未知的系统,我们假设它有n个参数。我们想要求出那些参数最重要,而把不重要的参数给抹掉,从而降低参数向量的维数。PCA的问题其实是一个基的变换,使得变换后的数据有着最大的方差。


1.假设有2个参数xy,我们通过观察n次,已经得到了n个xy的值。

2.求出xy的协方差矩阵COVMatrix


3.求出COVMatrix的特征向量eigenvectors以及特征值eigenvalues
4.若特征值大,则说明参数空间中的点更接近该特征值对应的特征向量。如图3.2

5.将所求出的特征向量组合成特征向量矩阵如上图。

6.用特征向量矩阵的转置左乘原始参数矩阵的转置 = (原始数据在以特征向量为基的坐标系下的坐标。
7.若FeatureVector不是全部的特征向量,则成为主成分,省去的其余成分都是非主要成分.
三、为什么要计算协方差1、最大方差理论
在信号处理中认为信号具有较大的方差,噪声有较小的方差,信噪比就是信号与噪声的方差比,越大越好。如前面的图,样本在横轴上的投影方差较大,在纵轴上的投影方差较小,那么认为纵轴上的投影是由噪声引起的。
因此我们认为,最好的k维特征是将n维样本点转换为k维后,每一维上的样本方差都很大。
比如下图有5个样本点:(已经做过预处理,均值为0,特征方差归一)
![clip_image026[4] clip_image026[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110513465.png)
下面将样本投影到某一维上,这里用一条过原点的直线表示(前处理的过程实质是将原点移到样本点的中心点)。
![clip_image028[4] clip_image028[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/20110418211051367.jpg)
假设我们选择两条不同的直线做投影,那么左右两条中哪个好呢?根据我们之前的方差最大化理论,左边的好,因为投影后的样本点之间方差最大。
这里先解释一下投影的概念:
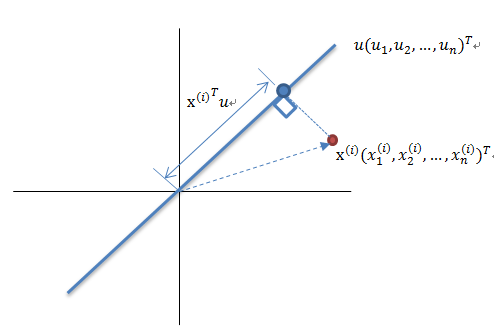
红色点表示样例![]() ,蓝色点表示
,蓝色点表示![]() 在u上的投影,u是直线的斜率也是直线的方向向量,而且是单位向量。蓝色点是
在u上的投影,u是直线的斜率也是直线的方向向量,而且是单位向量。蓝色点是![]() 在u上的投影点,离原点的距离是
在u上的投影点,离原点的距离是![]() (即
(即![]() 或者
或者![]() )由于这些样本点(样例)的每一维特征均值都为0,因此投影到u上的样本点(只有一个到原点的距离值)的均值仍然是0。
)由于这些样本点(样例)的每一维特征均值都为0,因此投影到u上的样本点(只有一个到原点的距离值)的均值仍然是0。
回到上面左右图中的左图,我们要求的是最佳的u,使得投影后的样本点方差最大。
由于投影后均值为0,因此方差为:
![clip_image042[4] clip_image042[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182110578868.png)
中间那部分很熟悉啊,不就是样本特征的协方差矩阵么(![]() 的均值为0,一般协方差矩阵都除以m-1,这里用m)。
的均值为0,一般协方差矩阵都除以m-1,这里用m)。
用![]() 来表示
来表示![]() ,
,![]() 表示
表示![]() ,那么上式写作
,那么上式写作
![]()
由于u是单位向量,即![]() ,上式两边都左乘u得,
,上式两边都左乘u得,![]()
即![]()
We got it!![]() 就是
就是![]() 的特征值,u是特征向量。最佳的投影直线是特征值
的特征值,u是特征向量。最佳的投影直线是特征值![]() 最大时对应的特征向量,其次是
最大时对应的特征向量,其次是![]() 第二大对应的特征向量,依次类推。
第二大对应的特征向量,依次类推。
因此,我们只需要对协方差矩阵进行特征值分解,得到的前k大特征值对应的特征向量就是最佳的k维新特征,而且这k维新特征是正交的。得到前k个u以后,样例![]() 通过以下变换可以得到新的样本。
通过以下变换可以得到新的样本。
![clip_image059[4] clip_image059[4]](http://images.cnblogs.com/cnblogs_com/jerrylead/201104/201104182111061880.png)
其中的第j维就是![]() 在
在![]() 上的投影。
上的投影。
通过选取最大的k个u,使得方差较小的特征(如噪声)被丢弃。
2、最小平方误差理论
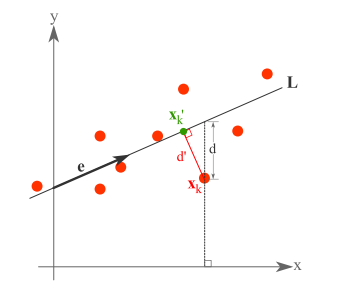
假设有这样的二维样本点(红色点),回顾我们前面探讨的是求一条直线,使得样本点投影到直线上的点的方差最大。本质是求直线,那么度量直线求的好不好,不仅仅只有方差最大化的方法。再回想我们最开始学习的线性回归等,目的也是求一个线性函数使得直线能够最佳拟合样本点,那么我们能不能认为最佳的直线就是回归后的直线呢?回归时我们的最小二乘法度量的是样本点到直线的坐标轴距离。比如这个问题中,特征是x,类标签是y。回归时最小二乘法度量的是距离d。如果使用回归方法来度量最佳直线,那么就是直接在原始样本上做回归了,跟特征选择就没什么关系了。
因此,我们打算选用另外一种评价直线好坏的方法,使用点到直线的距离d’来度量。
现在有n个样本点![]() ,每个样本点为m维(这节内容中使用的符号与上面的不太一致,需要重新理解符号的意义)。将样本点
,每个样本点为m维(这节内容中使用的符号与上面的不太一致,需要重新理解符号的意义)。将样本点![]() 在直线上的投影记为
在直线上的投影记为![]() ,那么我们就是要最小化
,那么我们就是要最小化
![]()
这个公式称作最小平方误差(Least Squared Error)。
而确定一条直线,一般只需要确定一个点,并且确定方向即可。
第一步确定点:
假设要在空间中找一点![]() 来代表这n个样本点,“代表”这个词不是量化的,因此要量化的话,我们就是要找一个m维的点
来代表这n个样本点,“代表”这个词不是量化的,因此要量化的话,我们就是要找一个m维的点![]() ,使得
,使得
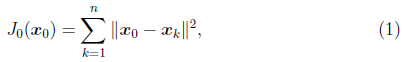
最小。其中![]() 是平方错误评价函数(squared-error criterion function),假设m为n个样本点的均值:
是平方错误评价函数(squared-error criterion function),假设m为n个样本点的均值:

那么平方错误可以写作:

后项与![]() 无关,看做常量,而
无关,看做常量,而![]() ,因此最小化
,因此最小化![]() 时,
时,
![]()
![]() 是样本点均值。
是样本点均值。
第二步确定方向:
我们从![]() 拉出要求的直线(这条直线要过点m),假设直线的方向是单位向量e。那么直线上任意一点,比如
拉出要求的直线(这条直线要过点m),假设直线的方向是单位向量e。那么直线上任意一点,比如![]() 就可以用点m和e来表示
就可以用点m和e来表示
![]()
其中![]() 是
是![]() 到点m的距离。
到点m的距离。
我们重新定义最小平方误差:
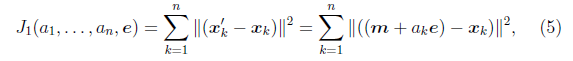
这里的k只是相当于i。![]() 就是最小平方误差函数,其中的未知参数是
就是最小平方误差函数,其中的未知参数是![]() 和e。
和e。
实际上是求![]() 的最小值。首先将上式展开:
的最小值。首先将上式展开:
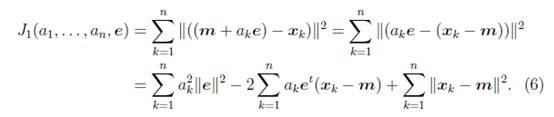
我们首先固定e,将其看做是常量,![]() ,然后对
,然后对![]() 进行求导,得
进行求导,得
![]()
这个结果意思是说,如果知道了e,那么将![]() 与e做内积,就可以知道了
与e做内积,就可以知道了![]() 在e上的投影离m的长度距离,不过这个结果不用求都知道。
在e上的投影离m的长度距离,不过这个结果不用求都知道。
然后是固定![]() ,对e求偏导数,我们先将公式(8)代入
,对e求偏导数,我们先将公式(8)代入![]() ,得
,得
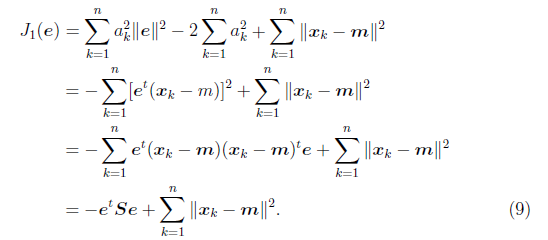
其中![]() 与协方差矩阵类似,只是缺少个分母n-1,我们称之为散列矩阵(scatter matrix)。
与协方差矩阵类似,只是缺少个分母n-1,我们称之为散列矩阵(scatter matrix)。
然后可以对e求偏导数,但是e需要首先满足![]() ,引入拉格朗日乘子
,引入拉格朗日乘子![]() ,来使
,来使![]() 最大(
最大(![]() 最小),令
最小),令
![]()
求偏导
![]()
这里存在对向量求导数的技巧,方法这里不多做介绍。可以去看一些关于矩阵微积分的资料,这里求导时可以将![]() 看作是
看作是![]() ,将
,将![]() 看做是
看做是![]() 。
。
导数等于0时,得
![]()
两边除以n-1就变成了,对协方差矩阵求特征值向量了。
从不同的思路出发,最后得到同一个结果,对协方差矩阵求特征向量,求得后特征向量上就成为了新的坐标,如下图:
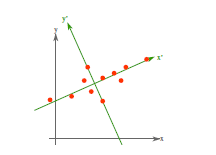
这时候点都聚集在新的坐标轴周围,因为我们使用的最小平方误差的意义就在此。
- PCA原理以及为何要使用协方差矩阵
- PCA为什么使用协方差矩阵
- 协方差矩阵与PCA深入原理剖析
- PCA为什么要用协方差矩阵?
- PCA与协方差矩阵
- 协方差矩阵以及最大方差理论在pca中的应用
- 从协方差矩阵到PCA
- 协方差矩阵和PCA的科普文
- PCA中关于协方差矩阵的问题
- 向量表示,投影,协方差矩阵,PCA
- 从协方差矩阵角度看PCA
- 协方差以及协方差矩阵的理解
- 向量的表示及协方差矩阵 (PCA的理论基础)
- 协方差矩阵与主成分分析(PCA)
- 向量的表示、投影、变换、协方差矩阵及PCA
- 主成分分析PCA之协方差矩阵的理解
- 均值,方差,协方差三者的关系以及协方差矩阵
- Matlab协方差矩阵的计算原理
- 可视化——matplotlib常用api(一)
- Linux kernel crash dumps with crash
- 杭电校赛(ACM组队安排)
- Duplicate files copied in APK META-INF/解决方式
- ubuntu14配置jdk1.7
- PCA原理以及为何要使用协方差矩阵
- 数据库之三大范式
- 反编译APK文件
- SecureCRT 绝佳配色方案, 保护你的眼睛
- Android官方文档翻译 九 2.2Adding Action Buttons
- TeamTalk——ubuntu服务端部署
- C++ 对文件夹的操作
- CSS属性的陷阱
- 单源点最短路径


