codeforces 424D. Biathlon Track（dp+ brute force)

http://codeforces.com/problemset/problem/424/D

Recently an official statement of the world Olympic Committee said that the Olympic Winter Games 2030 will be held in Tomsk. The city officials decided to prepare for the Olympics thoroughly and to build all the necessary Olympic facilities as early as possible. First, a biathlon track will be built.

To construct a biathlon track a plot of land was allocated, which is a rectangle divided inton × m identical squares. Each of the squares has two coordinates: the number of the row (from 1 ton), where it is located, the number of the column (from 1 tom), where it is located. Also each of the squares is characterized by its height. During the sports the biathletes will have to move from one square to another. If a biathlete moves from a higher square to a lower one, he makes a descent. If a biathlete moves from a lower square to a higher one, he makes an ascent. If a biathlete moves between two squares with the same height, then he moves on flat ground.

The biathlon track should be a border of some rectangular area of the allocated land on which biathletes will move in the clockwise direction. It is known that on one move on flat ground an average biathlete spendst_p seconds, an ascent takest_u seconds, a descent takest_d seconds. The Tomsk Administration wants to choose the route so that the average biathlete passes it in as close tot seconds as possible. In other words, the difference between timet_s of passing the selected track andt should be minimum.

For a better understanding you can look at the first sample of the input data. In this samplen = 6, m = 7, and the administration wants the track covering time to be as close tot = 48 seconds as possible, also, t_p = 3, t_u = 6 and t_d = 2. If we consider the rectangle shown on the image by arrows, the average biathlete can move along the boundary in a clockwise direction in exactly48 seconds. The upper left corner of this track is located in the square with the row number4, column number 3 and the lower right corner is at square with row number6, column number 7.

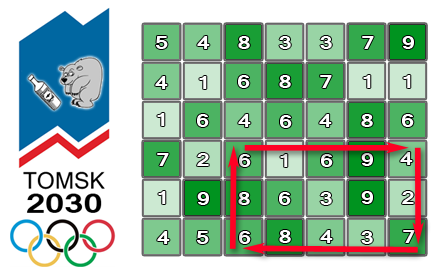
Among other things the administration wants all sides of the rectangle which boundaries will be the biathlon track to consist of no less than three squares and to be completely contained within the selected land.

You are given the description of the given plot of land and all necessary time values. You are to write the program to find the most suitable rectangle for a biathlon track. If there are several such rectangles, you are allowed to print any of them.

Input

The first line of the input contains three integers n,m and t (3 ≤ n, m ≤ 300,1 ≤ t ≤ 10⁹) — the sizes of the land plot and the desired distance covering time.

The second line also contains three integers t_p,t_u andt_d (1 ≤ t_p, t_u, t_d ≤ 100) — the time the average biathlete needs to cover a flat piece of the track, an ascent and a descent respectively.

Then n lines follow, each line containsm integers that set the heights of each square of the given plot of land. Each of the height values is a positive integer, not exceeding10⁶.

Output

In a single line of the output print four positive integers — the number of the row and the number of the column of the upper left corner and the number of the row and the number of the column of the lower right corner of the rectangle that is chosen for the track.

Sample test(s)

Input

6 7 483 6 25 4 8 3 3 7 94 1 6 8 7 1 11 6 4 6 4 8 67 2 6 1 6 9 41 9 8 6 3 9 24 5 6 8 4 3 7

Output

4 3 6 7

分析：

行走的四个方向有不同的分值结果，用dp存储每个点的计算结果（选择四边的点作为计算的起点），然后直接暴力求解（过得很凶险，本来也想用排序后的写法做的但是没过）。

#include <iostream>#include <cstdio>#include <cstring>using namespace std;int gra[305][305];int dp[305][305][4];int n,m,t;int tp,tu,td;  //  平  高  降int work(int a,int b){     if(a==b) return tp;     if(a<b) return tu;     return td;}int abs(int a){    return a<0?-a:a;}int main(){    while(~scanf("%d%d%d",&n,&m,&t)){         memset(dp,0,sizeof(dp));         scanf("%d%d%d",&tp,&tu,&td);         for(int i=1;i<=n;i++){            for(int j=1;j<=m;j++){                scanf("%d",&gra[i][j]);            }         }         for(int j=2;j<=m;j++){            for(int i=1;i<=n;i++){                dp[i][j][0]=dp[i][j-1][0]+work(gra[i][j-1],gra[i][j]);            }         }         for(int j=m-1;j>=1;j--){            for(int i=1;i<=n;i++){                dp[i][j][2]=dp[i][j+1][2]+work(gra[i][j+1],gra[i][j]);            }         }         for(int i=2;i<=n;i++){            for(int j=1;j<=m;j++){                dp[i][j][1]=dp[i-1][j][1]+work(gra[i-1][j],gra[i][j]);            }         }         for(int i=n-1;i>=1;i--){            for(int j=1;j<=m;j++){                dp[i][j][3]=dp[i+1][j][3]+work(gra[i+1][j],gra[i][j]);            }         }         int dtime=0x3f3f3f3f;         int p1x=0,p1y=0,p2x=0,p2y=0;         for(int i=1;i<=n;i++){            for(int j=1;j<=m;j++){                for(int ii=i+2;ii<=n;ii++){                    for(int jj=j+2;jj<=m;jj++){                        int t0=dp[i][jj][0]-dp[i][j][0];                        int t1=dp[ii][jj][1]-dp[i][jj][1];                        int t2=dp[ii][j][2]-dp[ii][jj][2];                        int t3=dp[i][j][3]-dp[ii][j][3];                        int dt=t0+t1+t2+t3;                        int r=abs(dt-t);                        if(r<dtime){                            dtime=r;                            p1x=i;                            p1y=j;                            p2x=ii;                            p2y=jj;                            if(dtime==0){                                goto tag;                            }                        }                    }                }            }         }         tag:             printf("%d %d %d %d\n",p1x,p1y,p2x,p2y);    }    return 0;}