数据结构与算法 LeetCode编程练习--counts Prime

Description:

Count the number of prime numbers less than a non-negative number, n.

Credits:
Special thanks to @mithmatt for adding this problem and creating all test cases.

Hint:

1. Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n²). Could we do better?

2. As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better?

3. Let's write down all of 12's factors:

   2 × 6 = 123 × 4 = 124 × 3 = 126 × 2 = 12

   As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.

   Our total runtime has now improved to O(n^1.5), which is slightly better. Is there a faster approach?

   public int countPrimes(int n) {   int count = 0;   for (int i = 1; i < n; i++) {      if (isPrime(i)) count++;   }   return count;}private boolean isPrime(int num) {   if (num <= 1) return false;   // Loop's ending condition is i * i <= num instead of i <= sqrt(num)   // to avoid repeatedly calling an expensive function sqrt().   for (int i = 2; i * i <= num; i++) {      if (num % i == 0) return false;   }   return true;}

4. The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.

   
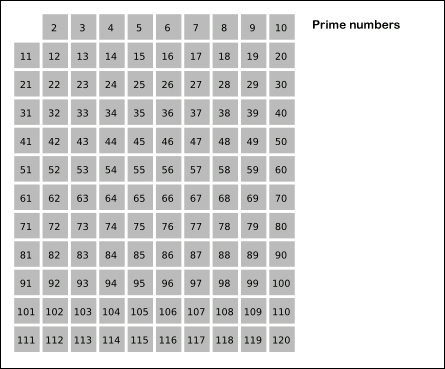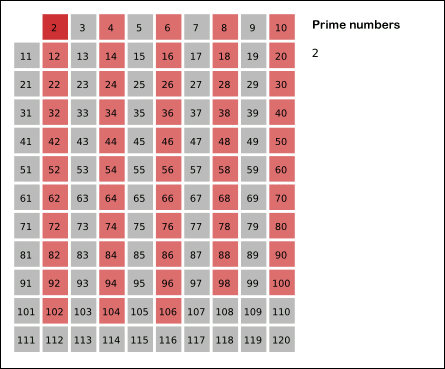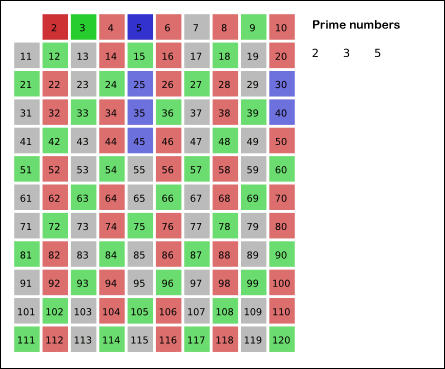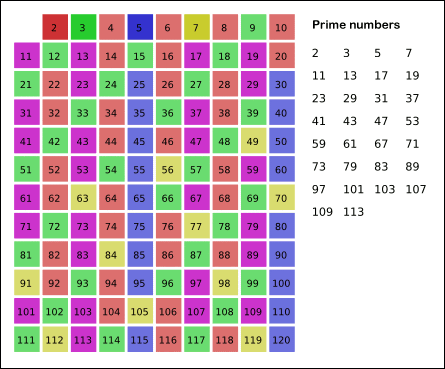
   Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.

   We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well?

5. 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off?

6. In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p², then in increments of p: p² + p, p² + 2p, ... Now what should be the terminating loop condition?

7. It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3?

8. Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.

   The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.

   public int countPrimes(int n) {   boolean[] isPrime = new boolean[n];   for (int i = 2; i < n; i++) {      isPrime[i] = true;   }   // Loop's ending condition is i * i < n instead of i < sqrt(n)   // to avoid repeatedly calling an expensive function sqrt().   for (int i = 2; i * i < n; i++) {      if (!isPrime[i]) continue;      for (int j = i * i; j < n; j += i) {         isPrime[j] = false;      }   }   int count = 0;   for (int i = 2; i < n; i++) {      if (isPrime[i]) count++;   }   return count;}

Subscribe to see which companies asked this question

思路：一开始大概想到用map，set去做，后来想着还可以用动态内存数组去做。大概是这样，遇到一个质素，就把他的倍数标记下，或放到set里面，最后统计没有标记的。

遇到的很多问题：第一个是8 out：3 expected:4,我在vs上运行的结果是对的，提交的测试的结果却不对，后来发现是申请的数组，默认值不一样。所以又重新赋值了一遍。

第二个，越界的错误，显示的是陷入无限循环，其实是在(j*i < n) 其实是相乘后数太大越界为负数了，所以陷入了死循环。

第三个，计算499837（大概就是这个数）的时候少了几个。是我防止越界在后面加了（j*i)>0,导致中间一些较大的值没有测试到，后来又改了（j<根下（n）），还是不对这样就限制了一些虽然j大 但i小的值，虽然i*j<n,但被我排除了。

最后结果：

class Solution {
public:
    bool isPrime(int n)
    {
    for (int i = 2; i <= int(sqrt(double(n))); i++)
    {
    if (n%i == 0)
    return false;
    }
    return true;
    }
    
    int countPrimes(int n) {
int counts = 0;
bool *arr = new bool[n];
{
for (int i = 0; i<n; i++)
arr[i] = true;
}
for (int i = 2; i < n; i++)
{
if (arr[i])
{
for (int j = i;((j*i < n)&&(i < (int(sqrt(n))) + 1)); j++)
{
arr[j*i] = false;
}
}
}
for (int i = 2; i < n ; i++)
{
if ((arr[i]))
counts++;
}
return counts;
    }
};