最短路dijkstra算法详解：dijkstra（图解）（详

来源：互联网发布：centos7.0修改ssh端口编辑：程序博客网时间：2024/05/29 08:32

本人小白，如果有写的不恰当的地方，还请大家指出，共同进步学习。

--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

谈到最短路，对于我来讲最喜欢的算法不过floyd，无脑，简单，好理解。但是面向oj上边解题的方式来讲，floyd的复杂度常常面对超时的可能，这也使得同样好理解的dijkstra算法更受到青睐。很多最短路方面的题目，我个人觉得还是看到dijkstra的题解比较多，所以我这里详解最短路的第一个算法就决定是先说dijkstra了。

镇博图~~~~没错，这位学者就是狄克斯特拉。狄克斯特拉1930年5月11日生于荷兰鹿特丹的一个知识分子家庭，在兄弟姊妹4人中排行第三。他的父亲是一名化学家和发明家，曾担任荷兰化学会主席。他母亲则是一位数学家。他成功地设计并实现了在有障碍物的两个地点之间找出一条最短路径的高效算法，这个算法被命名为“狄克斯特拉算法”，解决了机器人学中的一个十分关键的问题，即运动路径规划问题，至今仍被广泛应用，被认为是利用“贪心法”(greedy method)设计算法的一个成功范例。

既然说是最短路，我们当然要有贪心的思想，这里狄克斯特拉完美的做到了这一点。那在算法当中，是如何利用这个贪心思想的呢？我们这里对应一个图来看。（图不咋好看，轻吐槽T T。）

我们假设2是起点，想要走到终点 4，显然我们有两种走法，而且显而易见，走2-> 1-> 4这条路是最短的。我们不希望走2->4这条路。我们通过1这个点，能把从2->4的路径复杂化（多走一步（多转个弯））但是却能够缩短路径耗时的操作，我们理解为松弛操作，我们完成dijkstra的整个算法的过程，无非就是不断的在松弛的过程。我们希望走的路径短，那我们必然要走很多弯路- -*

我们这里对应完整算法的图来理解：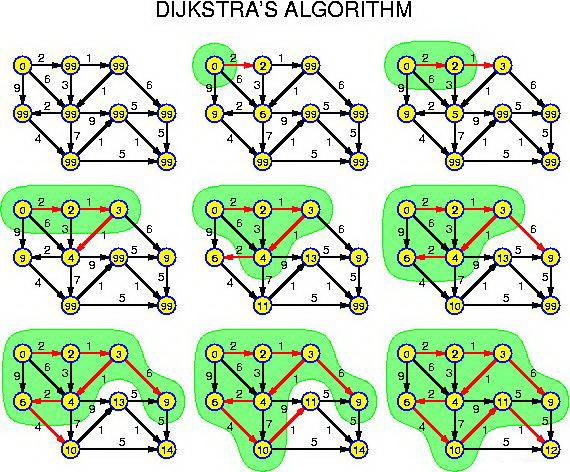

我们这里定义图的编号为：

1 2 3

4 5 6

7 8 9

图1：初始化的图，其中包含边的权值（耗时）。（这里图是有向图）。

图2：确定起点，然后向能直接走到的点走一下，记录此时的估计值：2 6 9.。

图3：找到距离起点最近的点，是正东边的那个点，这时候我们耗费权值为2。然后我们进行松弛操作，从起点到其东南方的点直接到的权值耗费为6，但是我们通过刚刚选定的点，我们找到了到这个点更近的方式，所以这个时候我们说从起点到其东南方向的点的权值更新值从6变成了5。这个时候我们就完成了第一次松弛操作。

图4：依旧是找距离起点最近的点。然后松弛我们发现这个时候从起点到其东南方的点的耗费权值从5又变成了4.这个时候我们完成了第二个松弛。

之后的方式同上：选定距离起点最近的点v。然后通过点v进行松弛操作。我们发现能够通过增加走到目的地方式的复杂度（多转弯）的方式我们能够松弛掉权值，使得耗费的权值更小。

读者请自己跑一遍上边的图，大概的算法思维也就掌握了。

然后我们对应代码和图一起探究：

void Dij()//我们这里起点为1号编码点。我们这里的d[]表示从起点到这个点需要的权值。w[a][b]表示点a到点b这条边的权值.{int i,j,k,v,tmp;memset(vis,0,sizeof(vis));for(i=1;i<=n;i++)    d[i]=w[1][i];//对应图不难理解，对于起点的初始化d[1]=0;vis[1]=1;for(i=1;i<=n;i++)//控制连接点的次数，例如上图，九个点，就循环九次。{tmp=N;//这里N表示无穷大。也就是图上的99.for(j=1;j<=n;j++){if(tmp>d[j]&&!vis[j]){tmp=d[j];v=j;}}//每次我们都找到距离起点最近的点vvis[v]=1;for(k=1;k<=n;k++)//然后进行松弛操作。<pre name="code" class="cpp">我们这里的d[]表示从起点到这个点需要的权值//加以强调其含义。

{if(!vis[k])d[k]=min(d[k],d[v]+w[v][k]);}}}

上图为松弛操作的效果图。其中我加了两个蓝色的中途点，表示我们这三个点并不一定是像最初的图那样的三个点，他们其中是有复杂的行进路程的。这样我们就很容易看的出来，是如何进行松弛操作的了~。

对于dijkstra是否能解无向图的问题，这里答案很明确：可以，因为无向图就是特殊的有向图，也可以理解为双向图。这里我们对应HDU的2544进行练习：

最短路

Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 46167 Accepted Submission(s): 20348

Problem Description

在每年的校赛里，所有进入决赛的同学都会获得一件很漂亮的t-shirt。但是每当我们的工作人员把上百件的衣服从商店运回到赛场的时候，却是非常累的！所以现在他们想要寻找最短的从商店到赛场的路线，你可以帮助他们吗？

Input

输入包括多组数据。每组数据第一行是两个整数N、M（N<=100，M<=10000），N表示成都的大街上有几个路口，标号为1的路口是商店所在地，标号为N的路口是赛场所在地，M则表示在成都有几条路。N=M=0表示输入结束。接下来M行，每行包括3个整数A，B，C（1<=A,B<=N,1<=C<=1000）,表示在路口A与路口B之间有一条路，我们的工作人员需要C分钟的时间走过这条路。输入保证至少存在1条商店到赛场的路线。

Output

对于每组输入，输出一行，表示工作人员从商店走到赛场的最短时间

Sample Input

2 11 2 33 31 2 52 3 53 1 20 0

Sample Output

#include<stdio.h>#include<string.h>#include<iostream>using namespace std;#define N 0x1f1f1f1fint w[151][151];int d[155];int ans,vis[151];int n,m;void Dij(){    int i,j,k,v,tmp;    memset(vis,0,sizeof(vis));    for(i=1;i<=n;i++)        d[i]=w[1][i];    d[1]=0;    vis[1]=1;    for(i=1;i<=n;i++)    {        tmp=N;        for(j=1;j<=n;j++)        {            if(tmp>d[j]&&!vis[j])            {                tmp=d[j];                v=j;            }        }        vis[v]=1;        for(k=1;k<=n;k++)        {            if(!vis[k])            d[k]=min(d[k],d[v]+w[v][k]);        }    }}int main(){    while(~scanf("%d%d",&n,&m))    {        if(n==0&&m==0)break;        for(int i=1;i<=n;i++)        {            for(int j=1;j<=n;j++)            {                w[i][j]=0x1f1f1f1f;            }        }        for(int i=0;i<m;i++)        {            int a,b,dis;            scanf("%d%d%d",&a,&b,&dis);            if(w[a][b]>dis)            w[a][b]=w[b][a]=dis;        }        Dij();        printf("%d\n",d[n]);    }}

0 0