图知识

来源：互联网发布：淘宝网图标图片大全编辑：程序博客网时间：2024/05/18 15:30

图的基本知识

2013-02-05 12:32 1036人阅读评论(0) 收藏举报

 分类：
数据结构

版权声明：本文为博主原创文章，未经博主允许不得转载。

=================================图的定义和术语=============================

图是一种基本的数据结构，表示为，其中，表示图的顶点集；，表示边(弧)集，连接顶点，当为无序对时，表示无向图; 若为有序对，则表示以顶点为起始点指向的一条边，此时的图称为有向图；当每条边关联一个非负权重时，称为加权图。顶点的度： ，表示和顶点相关联的边的权重之和，当是无权图时表示和顶点相关联的边的数目，则图的degree matrix ，为对角阵，对角元素为；在有向图中，顶点的度又分为出度和入度，其中出度表示以顶点为起始点的所有相关联边的权重之和，入度表示以顶点为终点的所有相关联边的权重之和。

子图：若存在图，且，则称是的子图。

完全图：图的任意两个不同顶点之间都存在一条边则称为完全图，无向完全图的边数目为，有向完全图的边数为。

路径、回路：若从顶点到顶点存在一个顶点序列，其中，则称，间存在路径，路径长度就是路径上边的数目。当图是有向图时，顶点序列也必须是有向的。当第一个顶点和最后一个相同时，则称此路径为回路。

连通图：若图中的任意两个顶点都存在路径，则称为联通图，在有向图中，若从到以及从到都存在路径，则称为强连通图

PS.

以下都是按加权图进行介绍，当为无权图时，若则令，否则。

=============================图的存储====================================

1. 邻接矩阵表示

邻接矩阵用表示，是一个的矩阵，其中每个元素表示为。

2. 邻接表

对每个顶点，建立一个单链表，链表中的节点表示和此顶点相关联的边，可有效解决稀疏邻接矩阵的问题。

其基本数据结构：

定义头结点：vexdata | firstarc ，定义邻接点：adjdata | inf | nextarc ：

对于有向图，通常按顶点的出度进行构建的邻接表(每个顶点的链表结点数是顶点的初度)，若按顶点的入度进行构建，则称为逆邻接表。
分别用无向图和有向图构建邻接表，如下图所示：

(1) 无向加权图

对应的邻接表为：

(2) 有向加权图

对应的邻接表为：

逆邻接表为：

3. 十字链表

专门为有向图设计的一种链式存储结构，融合了邻接表和逆邻接表的结构, 可方便的求取某个顶点的出度和入度：

在顶点结点中有三个域：data域存储和顶点相关的信息，如顶点编号等；firstin和firstout为两个链域，分别指向以该结点为弧头和弧尾的第一个结点。

在边结点中有五个域：尾域（tailvex）和头域（headvex）分别表示弧尾和弧头这两个顶点在图中的的编号，inf包含边的信息如权重，链域hlink指向弧头相同的下一条弧，而链域tlink指向弧尾相同的下一条弧。

对于上述的有向加权图，其对应的十字链表表示为：

4. 邻接多重图

邻接多重图是无向图的一种存储结构，类似于有向图的十字链表表示方式，也是采用顶点与边的链表结构进行存储：

在顶点结点中有两个域：data域存储和顶点相关的信息，如顶点编号等；firstedge为链域，指向以和该结点相关联的第一条边。

在边结点中有六个域：mark为标记域，指示此边是否被搜索过，ivex和jvex分别表示和此边关联的两个顶点在图中的的编号，ilink指向和顶点ivex相关联的下一条边，ilink指向和顶点jvex相关联的下一条边，inf包含边的信息如权重。

================================图的遍历===================================

1. 深度优先搜索(Depth Fisrst Search)

从图中某个顶点出发，访问此顶点，然后依次从的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和有路径相通的顶点都被访问到。

[cpp] view plaincopy
//顶点Structure  
struct VexNode{  
   int vexdata;    
   struct EdgeNode *firstarc;   
}EdgeNode;  
  
//邻接点Structure  
struct EdgeNode{  
   int adjdata;    
   float inf;  
   struct EdgeNode *nextarc;   
}EdgeNode;  

采用邻接表表示的无向图的DFS遍历：

[cpp] view plaincopy
void DFSTraverse(Graph *G)  
{  
    int v = 0;  
    for (v = 0;  v < G.vexnum; v++)   
        visited[v] = FALSE; // 访问标志数组初始化  
          
    for (v=0; v<G.vexnum; ++v)   
    {  
        if (!visited[v])    
            DFS_Recursive(G, v) ;    // 对尚未访问的顶点调用DFS_Recursive  
        }  
}  

递归遍历：

[cpp] view plaincopy
//从顶点v出发，递归遍历所有和v连通的顶点  
void DFS_Recursive(Graph *G, int v, bool visited[])  
{  
    VisitFunc(v);   //访问顶点v  
    visited[v] = true;  
      
    EdgeNode *p= G[v].firstarc;  
    while(p != NULL)  
    {  
        if(!visited[p->adjdata])  
            DFS_Recursive(G, p, visited); //访问未被访问的邻接顶点  
        p = p->nextarc;  
    }  
}  

非递归遍历：

[cpp] view plaincopy
//采用辅助栈实现非递归DFS遍历  
void DFS_Non_Recursive(Graph *G,  int v,  bool visited[])  
{  
    stack<int> s;  
    s.push(v);  
      
    while(!s.empty())  
    {  
        int node = s.top();  
        s.pop();  
          
        if(!visited[node])  
        {  
            VisitFunc(node);  
            visited[node] = true;  
              
            EdgeNode *p= G[node].firstarc;  
            while(p != NULL)  
            {  
                if(!visited[p->adjdata]) //将所有未被访问的邻接顶点压栈  
                    s.push(p->adjdata);  
                p = p->nextarc;  
                }  
        }  
    }  
}  

2. 广度优先搜索(Breadth_First Search)

从某个顶点出发，访问此顶点，之后依次访问的所有未被访问过的邻接点，之后按这些顶点被访问的先后次序依次访问它们的邻接点，直至图中所有和有路径相通的顶点都被访问到。

[cpp] view plaincopy
//采用辅助队列实现非递归BFS遍历  
void DFS_Non_Recursive(Graph *G,  int v,  bool visited[])  
{  
    queue <int> q;  
    VisitFunc(v);  
    visited[v] = true;  
    q.push(v);  
      
    while(!q.empty())  
    {  
        int node = q.front();  
        q.pop();  
  
        EdgeNode *p= G[node].firstarc;  
        while(p != NULL)  
        {  
            if(!visited[p->adjdata]) //将所有未被访问的邻接顶点加入队列                
            {  
                VisitFunc(p->adjdata);  
                visited[p->adjdata] = true;  
                q.push(p->adjdata);  
            }  
            p = p->nextarc;  
         }  
    }  
}  

[cpp] view plaincopy
void BFSTraverse(Graph *G)  
{  
    int v = 0;  
    for (v = 0;  v < G.vexnum; v++)   
        visited[v] = FALSE; // 访问标志数组初始化  
          
    for (v=0; v<G.vexnum; ++v)   
    {  
        if (!visited[v])    
            BFS_Non_Recursive(G, v) ;    // 对尚未访问的顶点调用BFS_Non_Recursive  
        }  
}  

参考文献

[1] http://www.xinx.sdnu.edu.cn/sfzx/jpsykc/zzh/zzh07.html#(28)

[2] http://comic.sjtu.edu.cn/thucs/GD_jsj_002b/text/chapter07/

最近看了一些矩阵和谱聚类的知识，特在此简单记录一下。详细可以先看下参考文献。

首先看到的是孟岩写的三篇<理解矩阵>.

一：理解矩阵(一)

1:传统书籍空间的定义：存在一个集合，在这个集合上定义某某概念，然后满足某些性质”，就可以被称为空间。孟的空间包含四点：(1). 由很多（实际上是无穷多个）位置点组成；(2). 这些点之间存在相对的关系；(3). 可以在空间中定义长度、角度；4.这个空间可以容纳运动，这里我们所说的运动是从一个点到另一个点的移动（变换），而不是微积分意义上的“连续”性的运动。其中第四点最为重要，容纳运动时空间的本质。

2：“空间”是容纳运动的一个对象集合，而变换则规定了对应空间的运动。

3：线性空间中的任何一个对象，通过选取基和坐标的办法，都可以表达为向量的形式。

4：在线性空间中，当你选定一组基之后，不仅可以用一个向量来描述空间中的任何一个对象，而且可以用矩阵来描述该空间中的任何一个运动（变换）。而使某个对象发生对应运动的方法，就是用代表那个运动的矩阵，乘以代表那个对象的向量。矩阵的本质是运动的描述。

二：理解矩阵(二)

1：所谓变换，其实就是空间里从一个点（元素/对象）到另一个点（元素/对象）的跃迁。矩阵是线性空间里的变换的描述

2：对于一个线性变换，只要你选定一组基，那么就可以找到一个矩阵来描述这个线性变换。换一组基，就得到一个不同的矩阵。所有这些矩阵都是这同一个线性变换的描述，但又都不是线性变换本身。

3：所谓相似矩阵，就是同一个线性变换的不同的描述矩阵。如同对同一对象的多个引用。

三：理解矩阵(三)

1：对象的变换等价于坐标系的变换。或者说：固定坐标系下一个对象的变换等价于固定对象所处的坐标系变换。

三篇矩阵系列让我们从直觉上再度理解了矩阵，形象深刻。第一篇可以说是初谈空间与矩阵；第二篇相当于矩阵再描述；第三篇则为矩阵等价于坐标系。

四：谱聚类

在谈及谱聚类的问题时，首先需要回顾一些数学知识。

1:正交矩阵。A^TA=E，则A为正交矩阵。也就是A的行或者列向量为两两垂直的单位向量

2：正定矩阵。如果对于任意向量f，都有f^TMf> 0，则称M为正定矩阵。如果为大于等于0，则为半正定矩阵。

3：拉普拉斯矩阵：Laplace矩阵为图的度矩阵-图的邻近矩阵。它也是谱理论的基础。

其中：

定义：

方阵的谱：方阵作为线性算子，它的所有特征值的集合成为方阵的谱。

矩阵的谱半径：矩阵和其共轭转置乘积的最大特征值。

谱聚类：是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从而达到对样本数据聚类的目的。

3：谱聚类最初用于解决图的分割为题，图分割的目的是类间相似性最小，类内相似性最大。它是一个NP难解问题，它可以转换为最小化图的Laplace矩阵的特征值的问题，这个可以通过公式进行证明。如果分两类的话，此时最小的特征值所对应的特征向量中大于0的归属于一类，小于0的归属于另一类，就可以将图分割成为两部分了。

如果进行k分类，则需要得到k个最小的特征值所对应的特征向量(N×k)，每列为一个特征向量，每行代表一个样本点，此时对它进行k-means聚类，就可以将N个点聚成k类了。

4：谱聚类用于实际样本空间，只需将每个样本看做图的一个顶点，再将样本点的距离通过高斯核函数(径向基核函数)映射为相似性，每个点与其它点相似和为度就可以进行谱聚类了。

5：优点：(1)谱聚类能在任意形状的样本空间上进行聚类，且收敛于全局最优点。而像k-means算法和EM算法是建立在凸球形的样本空间上，当样本空间不凸时，算法会陷入“局部”最优。

(2) 谱聚类只需要数据之间的相似度矩阵就可以了，而不必像K-means那样要求数据必须是 N 维欧氏空间中的向量。

(3)RatioCut方法只考虑了类间相似性最小，而normalizedCut不仅考虑了类间还考虑了类内的相似性。

五：谱哈希

待续.....

参考文献：

1：理解矩阵(一)http://blog.csdn.net/myan/article/details/647511

2：理解矩阵(二) http://blog.csdn.net/myan/article/details/649018

3：理解矩阵(三) http://blog.csdn.net/myan/article/details/1865397

4：july的http://blog.csdn.net/v_july_v/article/details/40738211从拉普拉斯矩阵说到谱聚类

5：机器学习中谱聚类方法的研究：http://lamda.nju.edu.cn/conf/MLA07/files/YuJ.pdf；

从谱聚类说到拉普拉斯矩阵

0 引言

11月1日上午，机器学习班第7次课，邹博讲聚类（PPT），其中的谱聚类引起了自己的兴趣，他从最基本的概念：单位向量、两个向量的正交、方阵的特征值和特征向量，讲到相似度图、拉普拉斯矩阵，最后讲谱聚类的目标函数和其算法流程。

课后自己又琢磨了番谱聚类跟拉普拉斯矩阵，打算写篇博客记录学习心得，若有不足或建议，欢迎随时不吝指出，thanks。

1 矩阵基础

在讲谱聚类之前，有必要了解一些矩阵方面的基础知识。

1.0 理解矩阵的12点数学笔记

如果对矩阵的概念已经模糊，推荐国内一人写的《理解矩阵by孟岩》系列，其中，抛出了很多有趣的观点，我之前在阅读的过程中做了些笔记，如下：

“1、事实上，简而言之：矩阵是线性空间里的变换的描述，相似矩阵则对同一个线性变换的不同描述。那，何谓空间？本质而言，”空间是容纳运动的一个对象集合，而变换则规定了对应空间的运动”by孟岩。在线性空间选定基后，向量刻画对象的运动，运动则通过矩阵与向量相乘来施加。然，到底什么是基？坐标系也。

2、有了基，那么在(1)中所言的则应是：矩阵是线性空间里的变换的描述，相似矩阵则对同一个线性变换在不同基(坐标系)下的不同描述。出来了两个问题，一者何谓变换，二者不同基(坐标系)如何理解？所谓变换，即空间里从一个点（元素/对象）到另一个(元素对象)的跃迁，矩阵用来描述线性变换。基呢?通过前面已知，矩阵无非不过就是用来描述线性空间中的线性变换的一个东西而已，线性变换为名词，矩阵为描述它的形容词，正如描述同一个人长得好看可以用多个不同形容词"帅”"靓”描述，同一个线性变换也可以由多个不同的矩阵来描述，而由哪一个矩阵描述它，则由基（坐标系）确定。

3、前面说了基，坐标系也，形象表述则为角度，看一个问题的角度不同，描述问题得到的结论也不同，但结论不代表问题本身，同理，对于一个线性变换，可以选定一组基，得到一个矩阵描述它，换一组基，得到不同矩阵描述它，矩阵只是描述线性变换非线性变换本身，类比给一个人选取不同角度拍照。

4、前面都是说矩阵描述线性变换，然，矩阵不仅可以用来描述线性变换，更可以用来描述基(坐标系/角度)，前者好理解，无非是通过变换的矩阵把线性空间中的一个点给变换到另一个点上去，但你说描述基(把一个坐标系变换到另一个坐标系)，这可又是何意呢?实际上，变换点与变换坐标系，异曲同工!
（@坎儿井围脖：矩阵还可以用来描述微分和积分变换。关键看基代表什么，用坐标基就是坐标变换。如果基是小波基或傅里叶基，就可以用来描述小波变换或傅里叶变换）

5、矩阵是线性运动(变换)的描述，矩阵与向量相乘则是实施运动(变换)的过程，同一个变换在不同的坐标系下表现为不同的矩阵，但本质/征值相同，运动是相对的，对象的变换等价于坐标系的变换，如点(1,1)变到(2,3)，一者点动，二者让X轴单位度量长度变成原来1/2，让Y轴单位度量长度变成原来1/3。

6、Ma=b，点动则是向量a经过矩阵M所描述的变换，变成了向量b；变坐标系则是有一个向量，它在坐标系M的度量下结果为a，在坐标系I(I为单位矩阵，主对角为1，其它为0)的度量下结果为b，本质上点运动与变换坐标系两者等价。为何?如(6)所述，同一个变换，不同坐标系下表现不同矩阵，但本质相同。

7、Ib，I在(6)中说为单位坐标系，其实就是我们常说的直角坐标系，如Ma=Ib，在M坐标系里是向量a，在I坐标系里是向量b，本质上就是同一个向量，故此谓矩阵乘法计算无异于身份识别。且慢，什么是向量?放在坐标系中度量，后把度量的结果(向量在各个坐标轴上投影值)按顺序排列在一起，即成向量。

8、b在I坐标系中-〉Ib，a在M坐标系中-〉Ma，故而矩阵乘法MxN，不过是N在M坐标系中度量得到-〉MN，而M本身在I坐标系中度量出。故Ma=Ib，M坐标系中的a转过来在I坐标系中一量，却成了b。如向量(x,y)在单位长度均为1的直角坐标系中一量-〉(1,1)，在X轴单位长度为2.Y轴单位长度为3一量-〉(2,3)。

9、何谓逆矩阵? Ma=Ib，之前已明了点变换a-〉b等价于坐标系变换M-〉I，但具体M如何变为I呢，答曰让M乘以M的逆矩阵。以坐标系

为例，X轴单位度量长度变为原来的1/2，Y轴单位度量长度变为原来的1/3，即与矩阵

相乘，便成直角坐标系I。即对坐标系施加变换，即让其与变换矩阵相乘。 ”

1.1 一堆基础概念

根据wikipedia的介绍，在矩阵中，

n阶单位矩阵，是一个

的方形矩阵，其主对角线元素为1，其余元素为0。单位矩阵以

表示；如果阶数可忽略，或可由前后文确定的话，也可简记为

（或者E）。如下图所示，便是一些单位矩阵：

单位矩阵中的第

列即为单位向量

。单位向量同时也是单位矩阵的特征向量，特征值皆为1，因此这是唯一的特征值，且具有重数

。由此可见，单位矩阵的行列式为1，且迹数为

。

单位向量又是什么呢？数学上，赋范向量空间中的单位向量就是长度为 1 的向量。欧几里得空间中，两个单位向量的点积就是它们之间角度的余弦（因为它们的长度都是 1）。

一个非零向量

的正规化向量（即单位向量）

就是平行于

的单位向量，记作：

这里

是

的范数（长度）。

何谓点积？点积又称内积，两个向量

= [a1, a2,…, an]和

= [b1, b2,…, bn]的点积定义为：

这里的Σ指示求和符号。

例如，两个三维向量[1, 3, -5]和[4, -2, -1]的点积是

：

使用矩阵乘法并把（纵列）向量当作n×1 矩阵，点积还可以写为：

这里的

指示矩阵

的转置。使用上面的例子，将一个1×3矩阵（就是行向量）乘以一个3×1向量得到结果(通过矩阵乘法的优势得到1×1矩阵也就是标量)：

除了上面的代数定义外，点积还有另外一种定义：几何定义。在欧几里得空间中，点积可以直观地定义为：

这里||表示的模（长度），θ表示两个向量之间的角度。根据这个定义式可得：两个互相垂直的向量的点积总是零。若和都是单位向量（长度为1），它们的点积就是它们的夹角的余弦。

正交是垂直这一直观概念的推广，若内积空间中两向量的内积（即点积）为0，则称它们是正交的，相当于这两向量垂直，换言之，如果能够定义向量间的夹角，则正交可以直观的理解为垂直。而正交矩阵（orthogonal matrix）是一个元素为实数，而且行与列皆为正交的单位向量的方块矩阵（方块矩阵，或简称方阵，是行数及列数皆相同的矩阵。）

若数字

和非零向量

满足

，则

为

的一个特征向量，

是其对应的特征值。换句话说，在

这个方向上，

做的事情无非是把

沿其

的方向拉长/缩短了一点（而不是毫无规律的多维变换），

则是表示沿着这个方向上拉伸了多少的比例。简言之，

对

做了手脚，使得向量

变长或变短了，但

本身的方向不变。

矩阵的迹是

矩阵

的对角线元素之和，也是其

个特征值之和。

更多矩阵相关的概念可以查阅相关wikipedia，或《矩阵分析与应用》。

2 拉普拉斯矩阵

2.1 Laplacian matrix的定义

拉普拉斯矩阵（Laplacian matrix)），也称为基尔霍夫矩阵, 是表示图的一种矩阵。给定一个有n个顶点的图

，其拉普拉斯矩阵被定义为:

其中D为图的度矩阵，A为图的邻接矩阵。

举个例子。给定一个简单的图，如下：

则其度矩阵为：

其邻接矩阵为：

根据拉普拉斯矩阵的定义

，可得拉普拉斯矩阵为：

2.2 拉普拉斯矩阵的性质

拉普拉斯矩阵具有如下性质：

L 是对称半正定矩阵；
L 的最小特征值是0，相应的特征向量是
L 有n个非负实特征值
且对于f，有以下式子成立

下面，来证明下上述结论，如下：

更多拉普拉斯矩阵的性质请参考参考文献6：“A Tutorial on Spectral Clustering”。

3 谱聚类

聚类的直观解释是根据样本间各自的相似度，将它们分成不同组。

相当于如果将样本看作顶点，样本间的相似度看作带权的边，便可将聚类问题转换为图分割问题，而谱聚类的思想则是要找到一种图的分割方法，使得连接不同组的边的权重尽可能低（这意味着组间相似度要尽可能低），组内的边的权重尽可能高（这意味着组内相似度要尽可能高）。

简而言之，谱聚类就是要找到图的一个划分，形成若干个组(Group)，使得不同组之间有较低的权值，组内有较高的权值，从而达到常见的聚类目的。

为了更好的把谱聚类问题转换为图论问题，定义如下概念：

无向图G=(V,E)
邻接矩阵W
顶点的度d，形成一个度矩阵D （对角阵）

子图A的指示向量如下：

A组与B租之间所有边的权值之和定义如下：

其中，

定义为节点

到节点

的权值，如果两个节点不是相连的，权值为零。

3.1 目标函数

因此，如何切割图则成为问题的关键。换言之，如何切割才能得到最优的结果呢？

举个例子，如果用一张图片中的所有像素来组成一个图，并把（比如，颜色和位置上）相似的节点连接起来，边上的权值表示相似程度，现在要把图片分割为几个区域（或若干个组），要求是分割所得的 Cut 值最小，相当于那些被切断的边的权值之和最小，而权重比较大的边没有被切断。因为只有这样，才能让比较相似的点被保留在了同一个子图中，而彼此之间联系不大的点则被分割了开来。

为了让分割的Cut值最小，谱聚类便是要最小化下述目标函数：

其中k表示分成k个组，Ai表示第i个组，表示第Ai的补集，W(A,B)表示第A组与第B组之间的所有边的权重之和（换言之，如果要分成K个组，那么其代价就是进行分割时去掉的边的权值的总和）。

为了让被切断边的权值之和最小，便是要让上述目标函数最小化。但很多时候，最小化cut 通常会导致不好的分割。以分成2类为例，这个式子通常会将图分成了一个点和其余的n-1个点。为了让每个类都有合理的大小，目标函数应该显示的要求A1,A2...Ak足够大。

改进后的目标函数为：

其中|A|表示A组中包含的顶点数目。

或：

其中，。

4 参考文献与推荐阅读

孟岩之理解矩阵系列：http://blog.csdn.net/myan/article/details/1865397；
理解矩阵的12点数学笔记：http://www.51weixue.com/thread-476-1-1.html；
一堆wikipedia，比如特征向量：https://zh.wikipedia.org/wiki/%E7%89%B9%E5%BE%81%E5%90%91%E9%87%8F；
wikipedia上关于拉普拉斯矩阵的介绍：http://en.wikipedia.org/wiki/Laplacian_matrix；
邹博之聚类PPT：http://pan.baidu.com/s/1i3gOYJr；
关于谱聚类的一篇非常不错的英文文献，“A Tutorial on Spectral Clustering”：http://engr.case.edu/ray_soumya/mlrg/Luxburg07_tutorial_spectral_clustering.pdf；
知乎上关于矩阵和特征值的两个讨论：http://www.zhihu.com/question/21082351，http://www.zhihu.com/question/21874816；
谱聚类：http://www.cnblogs.com/fengyan/archive/2012/06/21/2553999.html；
谱聚类算法：http://www.cnblogs.com/sparkwen/p/3155850.html；
漫谈 Clustering 系列：http://blog.pluskid.org/?page_id=78；

原文链接:http://blog.csdn.net/v_july_v/article/details/40738211

图的拉普拉斯矩阵(Graph Laplacians)

2013-02-06 10:38 4568人阅读评论(0) 收藏举报

 分类：
图像/视觉（5） 

版权声明：本文为博主原创文章，未经博主允许不得转载。

Definition

如前述文章“图的基本知识”中所述，对于一个具有个顶点的图，用对角阵描述图各顶点的度，矩阵为其邻接矩阵，则定义Laplacian matrix为：

对于一个无向加权图( )，是对称阵且每个元素表示为：

其中为顶点的度，且。

【以下均针对无向加权图进行描述】

Properties

1. 是对称的半正定矩阵；

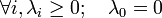2. 具有个非负的实数特征值： $\lambda_0 \le \lambda_1 \le \cdots \le \lambda_{n-1}$ ，且 $\forall i, \lambda_i \ge 0;\quad \lambda_0 = 0$ ，其对应的特征向量 $\mathbf{v_0}=[1,1,\dots,1]$ ；

3. 特征值为0的个数等于图连通分支的数目；

4. 对于任一为的向量，有：

具体证明过程可参见文献[2].

Normalized laplacian matrix

有两种Normalized 拉普拉斯矩阵：

(1) Symmetric normalized Laplacian

(2) Random walk normalized Laplacian

Applications

Spectral graph theory图谱论，就是借助于图的拉普拉斯矩阵的特征值和特征向量来研究图的性质，当前视觉领域的Spectral Clustering， Spectral Hashing，Graph Cut， Normalized Cut, Min-Cut等等技术都是通过Spectral graph theory来实现的。

参考文献

[1] http://en.wikipedia.org/wiki/Laplacian_matrix

[2]http://www.kyb.mpg.de/fileadmin/user_upload/files/publications/attachments/Luxburg07_tutorial_4488%5b0%5d.pdf

谱聚类Spectral Clustering

标签：聚类算法

2013-02-07 13:56 1233人阅读评论(0) 收藏举报

版权声明：本文为博主原创文章，未经博主允许不得转载。

Definition

spectral clustering techniques make use of thespectrum (eigenvalues) of thesimilarity matrix of the data to performdimensionality reduction before clustering in fewer dimensions. The goal of spectral clustering is to partition the dataset into disjoint subsets with high intra-cluster similarity and low inter-cluster similarity.

由此可见，谱聚类就是一个图分割问题。用无向图描述维空间的数据点集，，其中每条边关联一个权值，描述点和之间的相似度，则图的邻接矩阵可用相似度矩阵且表示。

Similarity graph&matrix

在维空间中，用一个相似度函数描述两点之间的相似度，如用高斯核 $G(v_i,v_j)=exp(-(\left \| x_i-x_j \right \|)^{2}/(2\sigma ^{2}))$ 计算相似度。相似度矩阵的构建过程就是描述数据点集中各数据点局部邻域关系图的过程，常用的构建方法有：

1. K-Nearest Neighbor

若是的KNN邻接点，则和之间存在一条边，with=，由于KNN不是相互的，即是的KNN邻接点但不一定是的KNN邻接点，由此产生的图就是一个有向图，为使其变为无向图常采用：(1) 直接忽略边的方向，即和只要存在一个方向的KNN邻接点对，则和就连接一条边，称为KNN-Graph；(2) 只有在和互为KNN邻接点时，和才连接一条边，称为Mutual KNN-Graph。

2. -Neighborhood

用阈值来描述一个点的邻域关系，即当与的距离小于时，和之间就存在一条边。

3. Full connected

任意的两点之间都存在一条边，与边关联的权值能够反映点之间的邻域关系，如高斯核 $G(v_i,v_j)=exp(-(\left \| x_i-x_j \right \|)^{2}/(2\sigma ^{2}))$ 中的就能控制邻域的大小。

基于上述3种邻域图的构建方法，相应的邻接矩阵也可随之产生。

Spectral clustering

基于上述构建的图和相似度矩阵，可采用拉普拉斯矩阵来执行谱聚类，具体过程如下：

(1) Unnormalized spectral clustering
Input: Dataset and the similarity matrix , number k of clusters to construct.

      • Construct a similarity graph by one of the ways described in the above section. Let be its weighted adjacency matrix.
      • Compute the unnormalized Laplacian .
      • Compute the first k eigenvalue of  and the corresponding eigenvectors .
      • Let  be the eigenvector matrix containing the vectors as columns.
      • For , let be the vector corresponding to the i-th row of thus is dimensions.
      • Cluster the points (  )with the k-means algorithm into clusters .

Output: Clusters with

By “the first k eigenvectors” we refer to the eigenvectors corresponding to the k smallest eigenvalues (exclude as it always be zero).

(2) Normalized spectral clustering with
Input: Dataset and the similarity matrix , number k of clusters to construct.

      • Construct a similarity graph by one of the ways described in the above section. Let be its weighted adjacency matrix.
      • Compute the unnormalized Laplacian .
      • Compute the first k generalized eigenvectors of the generalized eigenproblem .
      • Let  be the eigenvector matrix containing the vectors as columns.
      • For , let be the vector corresponding to the i-th row of thus is dimensions.
      • Cluster the points (  )with the k-means algorithm into clusters .

Output: Clusters with

As the normalized Laplacian Matrix , thus====》. So in fact the alogrithm works with normalized Laplacian Matrix .

(3) Normalized spectral clustering with
Input: Dataset and the similarity matrix , number k of clusters to construct.

      • Construct a similarity graph by one of the ways described in the above section. Let  be its weighted adjacency matrix.
      • Compute the normalized Laplacian ,.
      • Compute the first k eigenvalue of  andthe corresponding eigenvectors.

• Let be the eigenvector matrix containing the vectors as columns.

      • Normalize each row of     to norm 1 by
      • For , let  be the vector corresponding to the i-th row of  thus  is  dimensions.
      • Cluster the points ( )with the k-means algorithm into clusters.

Output: Clusters with

参考文献

[1] http://en.wikipedia.org/wiki/Spectral_clustering
[2]http://www.kyb.mpg.de/fileadmin/user_upload/files/publications/attachments/Luxburg07_tutorial_4488%5b0%5d.pdf
[3] http://csustan.csustan.edu/~tom/Lecture-Notes/Clustering/GraphLaplacian-tutorial.pdf
[4] https://cwiki.apache.org/MAHOUT/spectral-clustering.html

谱哈希spectral hashing

2013-02-19 17:35 3860人阅读评论(3) 收藏举报

 分类：
Hashing技术（3） 

版权声明：本文为博主原创文章，未经博主允许不得转载。

请先阅读有关图的基本知识，图的拉普拉斯矩阵分析以及谱聚类相关内容，谱哈希基于上述技术基础。

谱哈希对图像特征向量的编码过程可看做是图分割问题，借助于对相似图的拉普拉斯矩阵特征值和特征向量的分析可对图分割问题提供一个松弛解。由谱聚类可知，相似图拉普拉斯矩阵的特征向量实际上就是原始特征降维后的向量，但其并不是0-1的二值向量，可通过对特征向量进行阈值化产生spectral hashing的二值编码(The bits in spectral hashing are calculated by thresholding a subset of eigenvectors of Laplacians of the similar graph).

若原始特征向量空间用高斯核度量相似度，则令为二值化后的特征向量矩阵即经Spectral Hashing后的二值特征向量，则在低维Hamming空间的平均Hamming距离可表示为。此外，What makes good code?

(1) each bit has 50% chance of being 0 or 1;

(2) the bits are independent of each other(always relaxed to uncorrelated).

因此，spectral hashing的编码过程可描述为下述的优化问题(为了求解问题的方便，将二值中的0表示为-1)：

用Spectral 理论描述为：

若没有二值的约束，则上述优化问题就简化为是拉普拉斯矩阵的个最小特征值所对应的特征向量构成的矩阵，通过简单的Thresholding可获取Binary Code。

但上述的编码过程仅适用于训练集，而我们需要的是能够泛化到任意给定的out-of-example特征向量，因此引入来描述原始特征空间中数据点的概率分布，则上述的优化问题可表述为：

当暂不考虑二值化约束时，上述优化问题的解即是eigenfunctions of weighted Laplace-Beltramician operactor with minimal eigenvalue. And with proper normalization, the eigenvectors of the discrete Laplacian defined by points sampled from coverges to eigenfunctions of as .

因此，就转化为如何利用服从分布的个离散的数据点求取的特征方程的问题：

当是separable distribution时，即，亦即各维之间相互独立时，的特征方程具有outer product 形式：

即若是特征值对应的一维空间的特征方程，则是特征值对应的维空间的特征方程。特别的，针对区间内均匀可分离的分布，一维空间的特征值和特征向量可通过下式求得：

----------function (1)

， ----------function (2)

Summarize the spectral hashing alogrithm:

Input: data points and the hashed bits

Finding the principal components of the data using PCA;
Calculating the smallest single-dimension analytical eigenfunctions of along every PCA direction. This is done by evaluating the smallest eigenvalues for each direction using function (2), thus creating a list of eigenvalues, and then sorting this list to find the smallest eigenvalues; ???
Thresholding the analytical eigenfunctions at zero, to obtain binary codes.

分析:

Step1中PCA的主要作用是align the axes for data points, 也就是使数据点各维之间相互独立，符合seperate distribution;

Step2个人理解应该是先求取维数据点每一维均匀分布区间，然后利用方程(2)求取每一维对应的最小的个特征值，因此总计有个特征值。然后在个特征值中选取最小的个，并记录其所对应的向量维度及其特征值序号，即对；针对选取的各最小特征值，计算其对应的一维特征方程。

Step3是采用符号函数，对选取的特征方程进行二值化，产生二值码

由此可见，对图的次分割，每次都是选取维空间的某一维，并没有利用特征方程的outer-product的特性，paper 中的解释是二值化编码采用的是符号函数，且，因此一个bit的取值可由其它bits确定，失了去独立性。但其前提是建立在每一个bit对应的特征方程是由其它bits对应特征方程的outer-product，若bits之间不包含相同的特征方程，则还会继续保留各bits之间的独立性。因此outer-product的特征方程应该也可以利用。这仅是个人理解，具体效果还有待验证。

训练集的作用主要是产生每维对应的分布区间，利用记录的个最小特征值对应的维度与特征值序号对扩展至out-of-example。

参考文献

[1] http://www.cs.huji.ac.il/~yweiss/SpectralHashing/ 包含了paper和matlab源码

0 0