svm小结

SVM最基本的应用是分类。 求解最优的分类面，然后用于分类。

最优分类面的定义： 

对于SVM，存在一个分类面，两个点集到此平面的最小距离最大，两个点集中的边缘点到此平面的距离最大。

从直观上来看，下图左边的，肯定不是最优分类面；而右边的能让人感觉到其距离更大，使用的支撑点更多，至少使用了三个分类面，应该是最优分类面。

那么，是不是一个最优分类面需要两个或三个以上的点才能确定那？

这个要依据实际情况而定。

如下图，左图是由三个点，来确定的一个最优分类面，不同类别的两个点确定一个中心点，而同类的两个点可以确定方向向量。这个最优分类面，需要三个点。

但对于右图，直接获取不同类别的两个点的垂面，即是最优分类面。这个分类面，则需要两个点。

以上，情况的分析，使得求解最优分类面的思路，模式比较复杂。

若采用穷举法，至少需要以下过程。

先取不同类别的两个点，求解中心连线的垂面。如以上右图模式

然后判断其他点到此垂面的距离，若有更小的距离（或负值，即分类错误），则选取以上左图模式。

穷举所有点。采用最直接的方式处理，则其运算复杂度为 m*n*n， 若n > m.

这个还没有用到高维映射哪，如果再加上高维映射的处理，算法恐怕就更复杂了。所以，穷举法是不太现实的。

2. 从直观到数学推论

由直观到拟合：

直观上，存在一个最优的超平面。

那么，我们就假设这个最优面的公式是：

W * X + b = 0，

那么对于所有的点集x，

都存在平行于最优超平面，的点集的边界面

W * xi + b >= 1 或 W * xi + b <= -1, 这里 yi可以归一化为1，-1

最大化这两个平行超平面的距离。即

max  2 / ||w||

或者说是 最小化w，即 min ||w||

另外一个条件是 W * xi + b >= 1 或 W * xi + b <= -1。

这个有点超出平时用的计算方法了（如果没学过最优化理论），因既有求极值，又有不等式存在。这个是典型的QP（quandratic programming）二次规划问题。

高数里面有有关求极值的理论，采用的是拉格朗日乘子法，但其条件是等式。

所以，需要将不等式，转化为等式的形式。 方法就引入变量。

给每个点配上一个系数α，若是边界点，那么α就为大于0，否则就为0.

则 αi * yi * (W * xi + b) = 0.

从另一方面来讲，αi也可以看做是拉格朗日系数，采用拉格朗日乘子法，求极值。

由于αi也是未知的。所以，又需要求出αi。

即 min ( max L )， max L 是因为后面的超平面公式经过减号后变成了 <= 形式，其求和的最大值为0。

先对min求极值, 对w，和b进行微分。

推导出以下关系

（blog没公式编辑器，想偷懒只要剪贴了）

终于推出简单点的公式了。由min 到 max 也是一个对偶转换的过程，又称dual

求max极值，并且，只有一个等式约束条件，缺点就是未知变量也增加了。

接下来，就是用最优化的方法，求取极值了。

对未知变量，取一个初始值，然后用点集中的点，一个接一个的进行训练。

直至未知变量收敛。

3. SMO 解法

SVM 从简单边界分类思路，到复杂的拉格朗日求解。

其实，对于二次规划问题，有经典的最速下降法，牛顿法等最优化求解方法。而SMO是一个SVM的优化算法，避开了经典的二次规划问题。

消除w，转换为 αi 的求解。这是一个更加有效的求解方法

利用KKT条件，再加上一堆的推论，终于有以下公式：

还是这么多公式和术语，真是令我头疼。只能先记着，后面慢慢消化。

原理理解：

 αi *  αj  * ... 其实仍然是一个多元规划问题，所以，先多做几个假设：

1. 假设除 α1 之外，其他都是定值，那么据∑ni=1αiyi=0，  α1可以直接定下来，就无法进行优化了。

2. 若有 α1，  α2是变量，其他是常量， α2可以由 α1来表示，代入到目标函数中，就形成了一个一元二次函数。这样就能轻易地求极值了。其中，还是要考虑约束条件的：

αiα

i

0 <= ai <= C. 总之，求极值是方便可行多了。

采用此方法，选取不同的 αi,  αj求极值。 然后选取最大的。

SMO就是采用这种原理，只不过它不是依次或随机选取 α，而是采用启发式算法选取最优的两个维度。

 John C. Platt 的那篇论文 Fast Training of Support Vector Machines Using Sequential Minimal Optimization，有原理，有伪代码可以参考。

http://blog.pluskid.org/?page_id=683

介绍的也是比较深入浅出的。

3. SVM种类有哪些，适用场景及优缺点

SVM的空间复杂度：

SVM 是所占内存，是样本数据量的平方。

《A Tutorial on Support Vector Machines for Pattern Recognition》  1998KluwerAcademicPublishers,Boston，训练计算复杂度在O(Nsv^3+LNsv^2+d*L*Nsv)和O(d*L^2)之间，其中Nsv是支持向量的个数，L是训练集样本的个数，d是每个样本的维数(原始的维数，没有经过向高维空间映射之前的维数).

总的来讲，SVM的SMO算法根据不同的应用场景，其算法复杂度为~N 到~N^2.2之间，而chunking scale的复杂度为~N^1.2 到~N^3.4之间。一般SMO比chunking算法有一阶的优势。

线性SVM比非线性SVM的smo算法要慢一些。所以，据原著论文的测试，SMO算法，在线性svm上快1000倍，在非线性上快15倍。

对于SVM的SMO算法的内存需求时线性的，这使得其能适用比较大的训练集。

所以，如果数据量很大，SVM的训练时间就会比较长，如垃圾邮件的分类检测，没有使用SVM分类器，而是使用了简单的naive bayes分类器，或者是使用逻辑回归模型分类。

---------------------

其他观点：

SVM在小样本训练集上能够得到比其它算法好很多的结果。支持向量机之所以成为目前最常用，效果最好的分类器之一，在于其优秀的泛化能力，这是是因为其本身的优化目标是结构化风险最小，而不是经验风险最小，因此，通过margin的概念，得到对数据分布的结构化描述，因此减低了对数据规模和数据分布的要求。

SVM也并不是在任何场景都比其他算法好，对于每种应用，最好尝试多种算法，然后评估结果。如SVM在邮件分类上，还不如逻辑回归、KNN、bayes的效果好。

SVM各个参数的含义？

sigma: rbf核函数的参数，用于生成高维的特征，常用的有几种核函数，如径向核函数，线性核函数，这个也需要凭经验来选择。

C：惩罚因子。在最优化函数中，对离群点的惩罚因子，也是对离群点的重视程度体现。这个也是凭经验和实验来选择。

SVM种类：

C-SVM： 分类型SVM，需要调优的参数有惩罚因子C，核函数参数。 C的取值 10^-4, 10^-3, 10^-2,... 到 1, 5... 依次变大

nu-SVM： 分类型SVM, 在一定程度上与C-SVM相同，将惩罚因子C换成了因子nu。其最优化的函数略有不同。nu的取值是0-1，一般取值从0.1到0.8. 0代表样本落入间隔内的数目最小的情况，1代表样本可以落入间隔可以很多的情况。

wiki上的原话：

The main motivation for the nu versions of SVM is that it has a has a more meaningful interpretation. This is because nu represents an upper bound on the fraction of training samples which are errors (badly predicted) and a lower bound on the fraction of samples which are support vectors. Some users feel nu is more intuitive to use than C or epsilon. 

C-SVR: 用于回归的svm模型

nu-SVR：同上

---------------------------

4. 其他相关概念：

VC维：将N个点进行分类，如分成两类，那么可以有2^N种分法，即可以理解成有2^N个学习问题。若存在一个假设H，能准确无误地将2^N种问题进行分类。那么这些点的数量N，就是H的VC维。 这个定义真生硬，只能先记住。一个实例就平面上3个点的线性划分的VC维是3. 而平面上 VC维不是4，是因为不存在4个样本点，能被划分成2^4 = 16种划分法，因为对角的两对点不能被线性划分为两类。更一般地，在r 维空间中，线性决策面的VC维为r+1。

置信风险： 分类器对 未知样本进行分类，得到的误差。也叫期望风险。

经验风险： 训练好的分类器，对训练样本重新分类得到的误差。即样本误差

结构风险：[置信风险， 经验风险], 如(置信风险 + 经验风险) / 2

置信风险的影响因素有： 训练样本数目和分类函数的VC维。训练样本数目，即样本越多，置信风险就可以比较小；VC维越大，问题的解的种类就越多，推广能力就越差，置信风险也就越大。因此，提高样本数，降低VC维，才能降低置信风险。

而一般的分类函数，需要提高VC维，即样本的特征数据量，来降低经验风险，如多项式分类函数。如此就会导致置信风险变高，结构风险也相应变高。过学习overfit，就是置信风险变高的缘故。

结构风险最小化SRM(structured risk minimize)就是同时考虑经验风险与结构风险。在小样本情况下，取得比较好的分类效果。保证分类精度（经验风险）的同时，降低学习机器的 VC 维，可以使学习机器在整个样本集上的期望风险得到控制，这应该就是SRM的原则。

当训练样本给定时，分类间隔越大，则对应的分类超平面集合的 VC 维就越小。（分类间隔的要求，对VC维的影响）

根据结构风险最小化原则，前者是保证经验风险（经验风险和期望风险依赖于学习机器函数族的选择）最小，而后者使分类间隔最大，导致 VC 维最小，实际上就是使推广性的界中的置信范围最小，从而达到使真实风险最小。

训练样本在线性可分的情况下，全部样本能被正确地分类（咦这个不就是传说中的yi*(w*xi+b)）>=1的条件吗），即经验风险Remp 为 0 的前提下，通过对分类间隔最大化（咦，这个就是Φ（w）＝(1/2)*w*w嘛），使分类器获得最好的推广性能。

对于线性不可分的状况，可以允许错分。即对于离群点降低分类间隔。将距离原来的分类面越远，离群就越严重，这个距离，可以用一个值--松弛变量来表示，只有离群点才有松弛变量。当然，要对这个值加以限制，即在最小化函数里，加入一个惩罚项，里面还有一个可以人为设定的惩罚项C。当C无限的大，那么就退化为硬间隔问题，不允许有离群点，问题可能无解。若C=0，无视离群点。有时C值需要多次尝试，获取一个较好的值。 这个里面可分析还很多，后面再学习。

核函数作用：将完全不可分问题，转换为可分或达到近似可分的状态。

松弛变量：解决近似可分的问题。

一、线性分类器：

首先给出一个非常非常简单的分类问题（线性可分），我们要用一条直线，将下图中黑色的点和白色的点分开，很显然，图上的这条直线就是我们要求的直线之一（可以有无数条这样的直线）

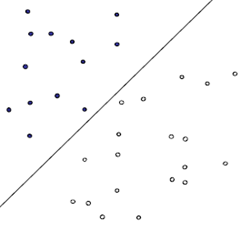假如说，我们令黑色的点 = -1， 白色的点 = +1，直线f(x) = w.x + b，这儿的x、w是向量，其实写成这种形式也是等价的f(x) = w1x1 + w2x2 … + wnxn + b, 当向量x的维度=2的时候，f(x) 表示二维空间中的一条直线， 当x的维度=3的时候，f(x) 表示3维空间中的一个平面，当x的维度=n > 3的时候，表示n维空间中的n-1维超平面。这些都是比较基础的内容，如果不太清楚，可能需要复习一下微积分、线性代数的内容。

刚刚说了，我们令黑色白色两类的点分别为+1, -1，所以当有一个新的点x需要预测属于哪个分类的时候，我们用sgn(f(x))，就可以预测了，sgn表示符号函数，当f(x) > 0的时候，sgn(f(x)) = +1, 当f(x) < 0的时候sgn(f(x)) = –1。

但是，我们怎样才能取得一个最优的划分直线f(x)呢？下图的直线表示几条可能的f(x)

一个很直观的感受是，让这条直线到给定样本中最近的点最远，这句话读起来比较拗口，下面给出几个图，来说明一下：

第一种分法：

第二种分法：

这两种分法哪种更好呢？从直观上来说，就是分割的间隙越大越好，把两个类别的点分得越开越好。就像我们平时判断一个人是男还是女，就是很难出现分错的情况，这就是男、女两个类别之间的间隙非常的大导致的，让我们可以更准确的进行分类。在SVM中，称为Maximum Marginal，是SVM的一个理论基础之一。选择使得间隙最大的函数作为分割平面是由很多道理的，比如说从概率的角度上来说，就是使得置信度最小的点置信度最大（听起来很拗口），从实践的角度来说，这样的效果非常好，等等。这里就不展开讲，作为一个结论就ok了，:)

上图被红色和蓝色的线圈出来的点就是所谓的支持向量(support vector)。

上图就是一个对之前说的类别中的间隙的一个描述。Classifier Boundary就是f(x)，红色和蓝色的线（plus plane与minus plane）就是support vector所在的面，红色、蓝色线之间的间隙就是我们要最大化的分类间的间隙。

这里直接给出M的式子：（从高中的解析几何就可以很容易的得到了，也可以参考后面Moore的ppt）

另外支持向量位于wx + b = 1与wx + b = -1的直线上，我们在前面乘上一个该点所属的类别y（还记得吗?y不是+1就是-1），就可以得到支持向量的表达式为：y(wx + b) = 1，这样就可以更简单的将支持向量表示出来了。

当支持向量确定下来的时候，分割函数就确定下来了，两个问题是等价的。得到支持向量，还有一个作用是，让支持向量后方那些点就不用参与计算了。这点在后面将会更详细的讲讲。

在这个小节的最后，给出我们要优化求解的表达式：

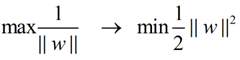
||w||的意思是w的二范数，跟上面的M表达式的分母是一个意思，之前得到，M = 2 / ||w||，最大化这个式子等价于最小化||w||, 另外由于||w||是一个单调函数，我们可以对其加入平方，和前面的系数，熟悉的同学应该很容易就看出来了，这个式子是为了方便求导。

这个式子有还有一些限制条件，完整的写下来，应该是这样的：（原问题）

s.t的意思是subject to，也就是在后面这个限制条件下的意思，这个词在svm的论文里面非常容易见到。这个其实是一个带约束的二次规划(quadratic programming, QP)问题，是一个凸问题，凸问题就是指的不会有局部最优解，可以想象一个漏斗，不管我们开始的时候将一个小球放在漏斗的什么位置，这个小球最终一定可以掉出漏斗，也就是得到全局最优解。s.t.后面的限制条件可以看做是一个凸多面体，我们要做的就是在这个凸多面体中找到最优解。这些问题这里不展开，因为展开的话，一本书也写不完。如果有疑问请看看wikipedia。

二、转化为对偶问题，并优化求解:

这个优化问题可以用拉格朗日乘子法去解，使用了KKT条件的理论，这里直接作出这个式子的拉格朗日目标函数：

求解这个式子的过程需要拉格朗日对偶性的相关知识（另外pluskid也有一篇文章专门讲这个问题），并且有一定的公式推导，如果不感兴趣，可以直接跳到后面用蓝色公式表示的结论，该部分推导主要参考自plukids的文章。

首先让L关于w，b最小化，分别令L关于w，b的偏导数为0，得到关于原问题的一个表达式

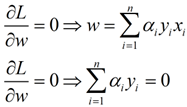
将两式带回L(w,b,a)得到对偶问题的表达式

新问题加上其限制条件是（对偶问题）:

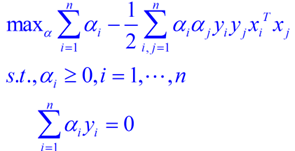
这个就是我们需要最终优化的式子。至此，得到了线性可分问题的优化式子。

求解这个式子，有很多的方法，比如SMO等等，个人认为，求解这样的一个带约束的凸优化问题与得到这个凸优化问题是比较独立的两件事情，所以在这篇文章中准备完全不涉及如何求解这个话题，如果之后有时间可以补上一篇文章来谈谈:)。

三、线性不可分的情况（软间隔）：

接下来谈谈线性不可分的情况，因为线性可分这种假设实在是太有局限性了：

下图就是一个典型的线性不可分的分类图，我们没有办法用一条直线去将其分成两个区域，每个区域只包含一种颜色的点。

要想在这种情况下的分类器，有两种方式，一种是用曲线去将其完全分开，曲线就是一种非线性的情况，跟之后将谈到的核函数有一定的关系：

另外一种还是用直线，不过不用去保证可分性，就是包容那些分错的情况，不过我们得加入惩罚函数，使得点分错的情况越合理越好。其实在很多时候，不是在训练的时候分类函数越完美越好，因为训练函数中有些数据本来就是噪声，可能就是在人工加上分类标签的时候加错了，如果我们在训练（学习）的时候把这些错误的点学习到了，那么模型在下次碰到这些错误情况的时候就难免出错了（假如老师给你讲课的时候，某个知识点讲错了，你还信以为真了，那么在考试的时候就难免出错）。这种学习的时候学到了“噪声”的过程就是一个过拟合（over-fitting），这在机器学习中是一个大忌，我们宁愿少学一些内容，也坚决杜绝多学一些错误的知识。还是回到主题，用直线怎么去分割线性不可分的点：

我们可以为分错的点加上一点惩罚，对一个分错的点的惩罚函数就是这个点到其正确位置的距离：

在上图中，蓝色、红色的直线分别为支持向量所在的边界，绿色的线为决策函数，那些紫色的线表示分错的点到其相应的决策面的距离，这样我们可以在原函数上面加上一个惩罚函数，并且带上其限制条件为：

公式中蓝色的部分为在线性可分问题的基础上加上的惩罚函数部分，当xi在正确一边的时候，ε=0，R为全部的点的数目，C是一个由用户去指定的系数，表示对分错的点加入多少的惩罚，当C很大的时候，分错的点就会更少，但是过拟合的情况可能会比较严重，当C很小的时候，分错的点可能会很多，不过可能由此得到的模型也会不太正确，所以如何选择C是有很多学问的，不过在大部分情况下就是通过经验尝试得到的。

接下来就是同样的，求解一个拉格朗日对偶问题，得到一个原问题的对偶问题的表达式：

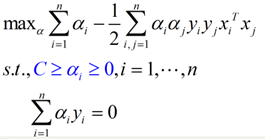
蓝色的部分是与线性可分的对偶问题表达式的不同之处。在线性不可分情况下得到的对偶问题，不同的地方就是α的范围从[0, +∞)，变为了[0, C]，增加的惩罚ε没有为对偶问题增加什么复杂度。

四、核函数：

刚刚在谈不可分的情况下，提了一句，如果使用某些非线性的方法，可以得到将两个分类完美划分的曲线，比如接下来将要说的核函数。

我们可以让空间从原本的线性空间变成一个更高维的空间，在这个高维的线性空间下，再用一个超平面进行划分。这儿举个例子，来理解一下如何利用空间的维度变得更高来帮助我们分类的（例子以及图片来自pluskid的kernel函数部分）：

下图是一个典型的线性不可分的情况

但是当我们把这两个类似于椭圆形的点映射到一个高维空间后，映射函数为：

用这个函数可以将上图的平面中的点映射到一个三维空间（z1,z2,z3)，并且对映射后的坐标加以旋转之后就可以得到一个线性可分的点集了。

用另外一个哲学例子来说：世界上本来没有两个完全一样的物体，对于所有的两个物体，我们可以通过增加维度来让他们最终有所区别，比如说两本书，从(颜色，内容)两个维度来说，可能是一样的，我们可以加上 作者 这个维度，是在不行我们还可以加入 页码，可以加入 拥有者，可以加入 购买地点，可以加入 笔记内容等等。当维度增加到无限维的时候，一定可以让任意的两个物体可分了。

回忆刚刚得到的对偶问题表达式：

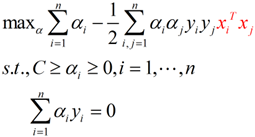
我们可以将红色这个部分进行改造，令：

这个式子所做的事情就是将线性的空间映射到高维的空间,k(x, xj)有很多种，下面是比较典型的两种：

上面这个核称为多项式核，下面这个核称为高斯核，高斯核甚至是将原始空间映射为无穷维空间，另外核函数有一些比较好的性质，比如说不会比线性条件下增加多少额外的计算量，等等，这里也不再深入。一般对于一个问题，不同的核函数可能会带来不同的结果，一般是需要尝试来得到的。

五、一些其他的问题：

1）如何进行多分类问题：

上面所谈到的分类都是2分类的情况，当N分类的情况下，主要有两种方式，一种是1 vs (N – 1)一种是1 vs 1，前一种方法我们需要训练N个分类器，第i个分类器是看看是属于分类i还是属于分类i的补集（出去i的N-1个分类）。

后一种方式我们需要训练N * (N – 1) / 2个分类器，分类器(i,j)能够判断某个点是属于i还是属于j。

这种处理方式不仅在SVM中会用到，在很多其他的分类中也是被广泛用到，从林教授（libsvm的作者）的结论来看，1 vs 1的方式要优于1 vs (N – 1)。

2）SVM会overfitting吗？

SVM避免overfitting，一种是调整之前说的惩罚函数中的C，另一种其实从式子上来看，min ||w||^2这个看起来是不是很眼熟？在最小二乘法回归的时候，我们看到过这个式子，这个式子可以让函数更平滑，所以SVM是一种不太容易over-fitting的方法。

最后简单地介绍一下用于优化 dual 问题的 Sequential Minimal Optimization (SMO) 方法。先回忆一下dual 问题：

maxαs.t.,∑i=1nαi–12∑i,j=1nαiαjyiyjκ(xi,xj)0≤αi≤C,i=1,…,n∑i=1nαiyi=0

对于变量 α 来说，这是一个 quadratic 函数。通常对于优化问题，我们没有办法的时候就会想到最笨的办法——Gradient Descent ，也就是梯度下降。注意我们这里的问题是要求最大值，只要在前面加上一个负号就可以转化为求最小值，所以 Gradient Descent 和 Gradient Ascend 并没有什么本质的区别，其基本思想直观上来说就是：梯度是函数值增幅最大的方向，因此只要沿着梯度的反方向走，就能使得函数值减小得越大，从而期望迅速达到最小值。当然普通的 Gradient Descent 并不能保证达到最小值，因为很有可能陷入一个局部极小值。不过对于 quadratic 问题，极值只有一个，所以是没有局部极值的问题。

另外还有一种叫做 Coordinate Descend 的变种，它每次只选择一个维度，例如 α=(α1,…,αn) ，它每次选取 αi 为变量，而将 α1,…,αi−1,αi+1,…,αn 都看成是常量，从而原始的问题在这一步变成一个一元函数，然后针对这个一元函数求最小值，如此反复轮换不同的维度进行迭代。Coordinate Descend 的主要用处在于那些原本很复杂，但是如果只限制在一维的情况下则变得很简单甚至可以直接求极值的情况，例如我们这里的问题，暂且不管约束条件，如果只看目标函数的话，当 α 只有一个分量是变量的时候，这就是一个普通的一元二次函数的极值问题，初中生也会做，带入公式即可。

然而这里还有一个问题就是约束条件的存在，其实如果没有约束条件的话，本身就是一个多元的 quadratic 问题，也是很好求解的。但是有了约束条件，结果让 Coordinate Descend 变得很尴尬了：比如我们假设 α1 是变量，而 α2,…,αn 是固定值的话，那么其实没有什么好优化的了，直接根据第二个约束条件 ∑ni=1αiyi=0 ，α1 的值立即就可以定下来——事实上，迭代每个坐标维度，最后发现优化根本进行不下去，因为迭代了一轮之后会发现根本没有任何进展，一切都停留在初始值。

所以 Sequential Minimal Optimization (SMO) 一次选取了两个坐标维度来进行优化。例如（不失一般性），我们假设现在选取 α1 和 α2 为变量，其余为常量，则根据约束条件我们有：

∑i=1nαiyi=0⇒α2=1y2(∑i=3nαiyi−α1y1)≜y2(K−α1y1)

其中那个从 3 到 n 的作和由于都是常量，我们统一记作 K ，然后由于 y∈{−1,+1} ，所以 y2 和 1/y2 是完全一样的，所以可以拿到分子上来。将这个式子带入原来的目标函数中，可以消去 α2 ，从而变成一个一元二次函数，具体展开的形式我就不写了，总之现在变成了一个非常简单的问题：带区间约束的一元二次函数极值问题——这个也是初中就学过求解方法的。唯一需要注意一点的就是这里的约束条件，一个就是 α1 本身需要满足 0≤α1≤C ，然后由于 α2也要满足同样的约束，即：

0≤y2(K−α1y1)≤C

也可以得到 α1 的一个可行区间，同 [0,C] 交集即可得到最终的可行区间。这个问题可以从图中得到一个直观的感觉。原本关于 α1 和 α2 的区间限制构成途中绿色的的方块，而另一个约束条件 y1α1+y2α2=K 实际上表示一条直线，两个集合的交集即是途中红颜色的线段，投影到 α1 轴上所对应的区间即是 α1 的取值范围，在这个区间内求二次函数的最大值即可完成 SMO 的一步迭代。

同 Coordinate Descent 一样，SMO 也会选取不同的两个 coordinate 维度进行优化，可以看出由于每一个迭代步骤实际上是一个可以直接求解的一元二次函数极值问题，所以求解非常高效。此外，SMO 也并不是依次或者随机地选取两个坐标维度，而是有一些启发式的策略来选取最优的两个坐标维度，具体的选取方法（和其他的一些细节），可以参见 John C. Platt 的那篇论文 Fast Training of Support Vector Machines Using Sequential Minimal Optimization 。关于 SMO ，我就不再多说了。如果你对研究实际的代码比较感兴趣，可以去看 LibSVM 的实现，当然，它那个也许已经不是原来版本的 SMO 了，因为本来 SVM 的优化就是一个有许多研究工作的领域，在那些主要的优化方法之上，也有各种改进的办法或者全新的算法提出来。

除了 LibSVM 之外，另外一个流行的实现 SVM^light 似乎是用了另一种优化方法，具体可以参考一下它相关的论文 Making large-Scale SVM Learning Practical 。

此外，虽然我们从 dual 问题的推导中得出了许多 SVM 的优良性质，但是 SVM 的数值优化（即使是非线性的版本）其实并不一定需要转化为 dual 问题来完成的，具体做法我并不清楚，不过这方面的文章也不少，比如 2007 年 Neural Computation 的一篇 Training a support vector machine in the primal 。如果感兴趣可以参考一下。 

转载地址：http://blog.csdn.net/viewcode/article/details/12840405

http://blog.csdn.net/sunanger_wang/article/details/7887218

http://blog.pluskid.org/?p=696