【poj3009】curling 2.0——dfs

题目：

Curling 2.0

Time Limit: 1000MS Memory Limit: 65536KTotal Submissions: 16112 Accepted: 6657

Description

On Planet MM-21, after their Olympic games this year, curling is getting popular. But the rules are somewhat different from ours. The game is played on an ice game board on which a square mesh is marked. They use only a single stone. The purpose of the game is to lead the stone from the start to the goal with the minimum number of moves.

Fig. 1 shows an example of a game board. Some squares may be occupied with blocks. There are two special squares namely the start and the goal, which are not occupied with blocks. (These two squares are distinct.) Once the stone begins to move, it will proceed until it hits a block. In order to bring the stone to the goal, you may have to stop the stone by hitting it against a block, and throw again.

Fig. 1: Example of board (S: start, G: goal)

The movement of the stone obeys the following rules:

• At the beginning, the stone stands still at the start square.
• The movements of the stone are restricted to x and y directions. Diagonal moves are prohibited.
• When the stone stands still, you can make it moving by throwing it. You may throw it to any direction unless it is blocked immediately(Fig. 2(a)).
• Once thrown, the stone keeps moving to the same direction until one of the following occurs:
  • The stone hits a block (Fig. 2(b), (c)).
    • The stone stops at the square next to the block it hit.
    • The block disappears.
  • The stone gets out of the board.
    • The game ends in failure.
  • The stone reaches the goal square.
    • The stone stops there and the game ends in success.
• You cannot throw the stone more than 10 times in a game. If the stone does not reach the goal in 10 moves, the game ends in failure.

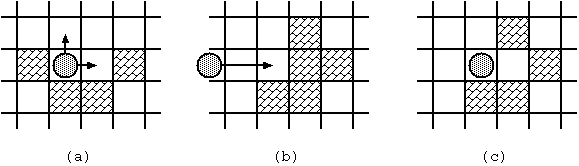
Fig. 2: Stone movements

Under the rules, we would like to know whether the stone at the start can reach the goal and, if yes, the minimum number of moves required.

With the initial configuration shown in Fig. 1, 4 moves are required to bring the stone from the start to the goal. The route is shown in Fig. 3(a). Notice when the stone reaches the goal, the board configuration has changed as in Fig. 3(b).

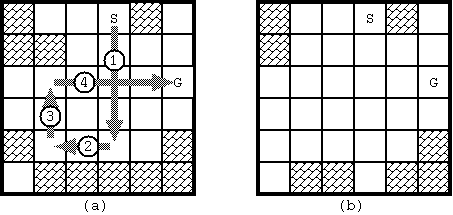
Fig. 3: The solution for Fig. D-1 and the final board configuration

Input

The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets never exceeds 100.

Each dataset is formatted as follows.

the width(=w) and the height(=h) of the board 
First row of the board 
... 
h-th row of the board

The width and the height of the board satisfy: 2 <= w <= 20, 1 <= h <= 20.

Each line consists of w decimal numbers delimited by a space. The number describes the status of the corresponding square.

0vacant square1block2start position3goal position

The dataset for Fig. D-1 is as follows:

6 6 
1 0 0 2 1 0 
1 1 0 0 0 0 
0 0 0 0 0 3 
0 0 0 0 0 0 
1 0 0 0 0 1 
0 1 1 1 1 1

Output

For each dataset, print a line having a decimal integer indicating the minimum number of moves along a route from the start to the goal. If there are no such routes, print -1 instead. Each line should not have any character other than this number.

Sample Input

2 13 26 61 0 0 2 1 01 1 0 0 0 00 0 0 0 0 30 0 0 0 0 01 0 0 0 0 10 1 1 1 1 16 11 1 2 1 1 36 11 0 2 1 1 312 12 0 1 1 1 1 1 1 1 1 1 313 12 0 1 1 1 1 1 1 1 1 1 1 30 0

Sample Output

14-1410-1

Source

Japan 2006 Domestic

描述：迷宫的升级版，首先起点和终点由题目给定，其次对于迷宫中的障碍物碰撞之后就会消失，第三迷宫的走法变成选择了某一方向之后只有碰到障碍物之后才会停下，停在碰撞的前一个然后等待下一次的方向选择。完成迷宫的条件变得更加苛刻，总的步数不能超过十步，走出了迷宫也算失败。

题解：一开始用了bfs，wa好多次发现不行，每次走过之后障碍物就消失了，但是如果是错误的选择就会是这部分的图失去真实性，因此应该选择dfs，在lose之后回溯把障碍物恢复原状再进行下一次尝试。把进行再次递归的条件写好了就没问题了。

代码：

#include<stdio.h>#include<cstring>int x[4] = { -1,0,1,0 };int y[4] = { 0,1,0,-1 };int n, m, i, j, sx, sy, ex, ey, ans;            //起点和终点的横纵坐标int p[21][21];int dfs(int sx, int sy, int ex, int ey, int t){if ((sx == ex) && (sy == ey)){if (t - 1 < ans) ans = t - 1;return 0;}if (t > 10) return 0;                       //记录每次步数int dx, dy;for (int i = 0; i < 4; i++){dx = sx + x[i];dy = sy + y[i];if (p[dx][dy] == 1)                     //旁边要是有障碍物是不能走的continue;while ((p[dx][dy] == 0) && (dx>0) && (dy > 0) && (dx <= n))//不满足条件就不再走了，剪枝{if ((dx == ex) && (dy == ey))       //每走一步都要检查是否满足了条件{if (t < ans) ans = t;           //更新结果return 0;}dx += x[i];dy += y[i];}if ((dx<1) || (dy<1) || (dx>n) || (dy>m))        //越界continue;p[dx][dy] = 0;dfs(dx - x[i], dy - y[i], ex, ey, t + 1);        //dfs一次次数加一，直接作为参数传递在过程中，及时更新答案，就不用开数组了p[dx][dy] = 1;                          //回溯回来要恢复！！！！}return 0;}int main(){scanf("%d %d", &m, &n);while ((n != 0) && (m != 0)){memset(p, 0, sizeof(p));for (i = 1; i <= n; i++)                   //m，n反过来，注意它们的意义for (j = 1; j <= m; j++){scanf("%d", &p[i][j]);if (p[i][j] == 2){sx = i;sy = j;p[i][j] = 0;}if (p[i][j] == 3){ex = i;ey = j;p[i][j] = 0;}}ans = 1000000;dfs(sx, sy, ex, ey, 1);if (ans != 1000000) printf("%d\n", ans);     //改变了，证明到过终点且是合法值else printf("-1\n");scanf("%d%d", &m, &n);}return 0;}