测试点是否在多边形内的方法总结

This is an early draft of the full articlepublished in Graphics Gems IV, the citation is:

     Haines, Eric, "Point in Polygon Strategies," Graphics Gems IV, ed. Paul Heckbert, Academic Press, p. 24-46, 1994.

(The full article is better, but I cannot find the final text on my machine.)The associatedcode for this articleis available online.

Testing whether a point is inside a polygon is a basic operation in computergraphics.Graphics Gems presents an algorithm for testing points againstconvex polygons(Badouel 1990). This Gem provides algorithms which are from1.6 to 9 or more times faster for convex polygons. It also presentsalgorithms for testing non-convex polygons and discusses the advantages anddrawbacks of each. Faster, more memory intensive algorithms are alsopresented, along with an O(log n) algorithm for convex polygons. Code isincluded for the algorithms discussed.

Polygon definition

There are two different types of polygons we will consider in this Gem:convex and non-convex. If a number of points are to be tested against apolygon, it may be worthwhile determining whether the polygon is convex at thestart and so be able to use a faster test. Another Gem (Schorn 1993)in this volume discusses ways of determining convexity.

Inside vs. Outside

One definition of whether a point is inside a region is the JordanCurve Theorem. Essentially, it says that a point is inside a polygon if, for anyray from this point, there is an odd number of crossings of the ray with thepolygon's edges (Figure 1). This definition means that some areas which areenclosed by a polygon are not considered inside. The center pentagonal areainside a star is classified as outside because any ray from this area willalways intersect an even number of edges.

If the entire area enclosed by the polygon is to be considered inside, thenthewinding number is used for testing. This value is the number oftimes the polygon goes around the point. For example, a point in the centerpentagonal area formed by a star has a winding number of two, since theoutline goes around it twice. If the point is outside, the polygon does notwind around it and so the winding number is zero. Winding numbers also have asign, which corresponds to the direction the edges wrap around the point.

Complex polygons can be formed using either polygon definition. A complexpolygon is one that has separate outlines (which can overlap). For example,the letter "R" can be defined by two polygons, one consisting of the exterioroutline, the other the inside hole in the letter. Most point in polygonalgorithms can be easily extended to test multiple outline polygons by simplyrunning each polygon outline through separately and keeping track of the totalparity.

3D to 2D

In ray tracing and other applications the original polygon is defined in threedimensions. To simplify computation it is worthwhile to project the polygonand test point into two dimensions. One way to do this is to simply ignoreone component. The best component to ignore is usually that which, whenignored, gives the largest area polygon. This is easily done by taking theabsolute value of each component of the polygon plane's normal and finding thelargest(Glassner 1989). The corresponding coordinates in thepolygon are then ignored. Precomputing some or all of this information oncefor a polygon uses more memory but increases the speed of the intersectiontest itself.

While the above method is simple and quick, another projection may be usefulwhen the polygon vertices are not guaranteed to lay on a single plane. Whilesuch polygons could be considered ill defined, they do crop up. For example,if a spline surface is tessellated into quadrilaterals instead of triangles,then the quadrilaterals are likely to be ill defined in this way. If acomponent is simply dropped, cracking can occur between such polygons whenthey are cast upon different planes.

One solution is to tessellate such polygons into triangles, but this may beimpractical for a variety of reasons. Another approach is to cast allpolygons tested onto a plane perpendicular to the testing ray's direction. Apolygon might have no area on this plane, but the ray would miss this polygonanyway. Casting a polygon onto an arbitrary plane means having to perform amatrix transformation, but this solution does provide a way around potentialcracking problems.

Bounding Areas

Point in polygon algorithms benefit from having a bounding box aroundpolygons with many edges. The point is first tested against this box beforethe full polygon test is performed; if the box is missed, so is the polygon.Most statistics generated in this Gem assume this bounding box test wasalready passed successfully.

In ray tracing, Worley (Worley 1993a) points out that the polygon's 3D bounding boxcan be treated like a 2D bounding box by throwing away one coordinate, as doneabove for polygons. By analysis of the operations involved, it can be shownto be generally more profitable to first intersect the polygon's plane thentest whether the point is inside the 2D bounding box rather than first testingthe 3D bounding box. Other bounding box variants can be found in Woo(Woo 1992).

Crossings Test

One algorithm for checking a point in any polygon is the crossings test. Theearliest presentation of this algorithm is Shimrat(Shimrat 1962), though it has a bugin it. A ray is shot from the test point along an axis (+X is commonly used)and the number of crossings is computed (Figure 1). Either the Jordan Curveor winding number test can be used to classify the point. What happens whenthe test ray intersects one or more vertices of the polygon? This problem canbe ignored by considering the test ray to be a half-plane divider, with one ofthe half-planes including the ray's points (Preparata 1985,Glassner 1989). In other words, whenever the ray wouldintersect a vertex, the vertex is always classified as being infinitesimallyabove the ray. In this way, no vertices are intersected and the code isboth simpler and speedier.

One way to think about this algorithm is to consider the test point to be atthe origin and to check the edges against this point. If the Y components ofa polygon edge differ in sign, then the edge can cross the test ray. In thiscase, if both X components are positive, the edge and ray must intersect and acrossing is recorded. Else, if the X signs differ, then the X intersectionof the edge and the ray is computed and if positive a crossing is recorded.

MacMartin (MacMartin 1992) pointed out that for polygons with a large number of edgesthere are generally runs of edges which have Y components with the same sign.For example, a polygon representing Brazil might have a thousand edges, butonly a few of these will straddle any given latitude line and there are longruns of contiguous edges on one side of the line. So a faster strategy is toloop through just the Y components as fast as possible; when they differ thenretrieve and check the X components. Compared to the basic crossings test theMacMartin test was up to 1.8 times faster for polygons up to 100 sides, withperformance particularly enhanced for polygons with many edges.

Other optimizations can be done for this test. Preprocessing the edge listinto separate X and Y component lists, with the first vertex added to the end,makes for particularly tight loops in the testing algorithm. This is not donein the code provided so as to avoid any preprocessing or additional memorycosts.

[Addenda: Joseph Samosky and Mark Haigh-Hutchinson submitted (unpublished)articles toGraphics Gems V.One idea these submissions inspired is a somewhat faster crossings test.By turning the division for testing the X axis crossinginto a tricky multiplication test this part of the test became faster,which had the additional effect of making the test for "both to left orboth to right" a bit slower for triangles than simply computing theintersection each time. The main increase is in triangle testing speed,which was about 15% faster; all other polygon complexities were pretty muchthe same as before. On machines where division is very expensive (not thecase on the HP 9000 series on which I tested) this test should be muchfaster overall than the old code. Your mileage may (in fact, will) vary,depending on the machine and the test data, but in general I believe thiscode is both shorter and faster. Related work by Samosky is in:Samosky, Joseph, "SectionView: A system for interactively specifying andvisualizing sections through three-dimensional medical image data",M.S. Thesis, Department of Electrical Engineering and Computer Science,Massachusetts Institute of Technology, 1993. Theroutine online is called the CrossingsMultiplyTest.]

Angle Summation Test

The worst algorithm in the world for testing points is the angle summationmethod. It's simple to describe: sum the signed angles formed at the pointby each edge's endpoints. If the sum is near zero, the point is outside; ifnot, it's inside (Figure 2). The winding number can be computed by findingthe nearest multiple of 360 degrees. The problem with this scheme is that itinvolves a square root, arc-cosine, division, dot and cross product for eachedge tested. In timing tests the MacMartin test was up to 63 times fasterthan the angle summation test for polygons with up to 100 sides. In fairness,the angle algorithm can be sped up in various ways, but it will still alwaysbe faster to use any other algorithm in this Gem.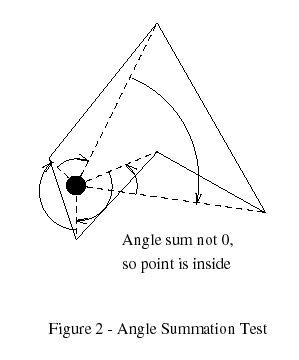

Triangle Tests

In Graphics Gems, Didier Badouel (Badoeul 1990) presents a method of testingpoints against convex polygons. The polygon is treated as a fan of trianglesemanating from one vertex and the point is tested against each triangle bycomputing its barycentric coordinates. As Berlin(Berlin 1985) points out, this testcan also be used for non-convex polygons by keeping a count of the number oftriangles which overlap the point; if odd, the point is inside the polygon(Figure 3). Unlike the convex test, where an intersection means that the testis done, all the triangles must be tested against the point for the non-convextest. Also, for the non-convex test there may be multiple barycentriccoordinates for a given point, since triangles can overlap.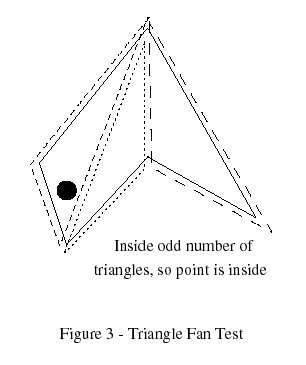

When the number of sides is small, the barycentric test is comparable to theMacMartin test in speed, with the additional bonus of having the barycentriccoordinates computed. As the number of sides approached 100, the MacMartintest becomes 3 to 6 times faster than the barycentric method.

A faster triangle fan tester proposed by Green (Green 1993) is to store a set ofhalf-plane equations for each triangle and test each in turn. If the point isoutside any of the three edges, it is outside the triangle. The half-planetest is an old idea, but storing the half-planes instead of deriving them onthe fly from the vertices gives this scheme its speed at the cost of someadditional storage space. For triangles this scheme is the fastest of all ofthe algorithms discussed so far, being almost twice as fast as the MacMartincrossings test. It is also very simple to code and so lends itself toassembly language translation.

Both the half-plane and barycentric triangle testers can be sped up further bysorting the order of the edge tests. Worley and Haines(Worley 1993b) note that thehalf-plane triangle test is more efficient if the longer edges are testedfirst. Larger edges tend to cut off more exterior area of the polygon'sbounding box, and so can result in earlier exit from testing a given triangle.Sorting in this way makes the test up to 1.6 times faster, rising quickly withthe number of edges in the polygon. However, polygons with a large number ofedges tend to bog down the sorted edge triangle algorithm, with the MacMartintest being from 1.6 to 2.2 times faster for 100 edge polygons.

For the general test a better ordering for each triangle's edges is to sort bythe area of the polygon's bounding box outside the edge, since we are tryingto maximize the amount of area discarded by each edge test. This orderingprovides up to another 10% savings in testing time. Unfortunately, for theconvex test below, this ordering actually loses about 10% for regular polygonsdue to a subtle quirk. As such, this ordering is not presented in thestatistics section or the code.

Convex Polygons

Convex polygons can be intersected faster due to their geometric properties.For example, the crossings test can quit as soon as two Y sign differenceedges are found, since this is the maximum that a convex polygon can have.Also, more polygons can be categorized as "convex" for the crossings test bychecking only the change in the Y direction (and not X and Y as for the fullconvexity test). For example, a block letter "E" has at most two Yintersections for any test point's horizontal line, so it can be treated asconvex when using the crossings test. Convexity is sufficient but notnecessary for all of the algorithms discussed in this section.

The triangle fan tests can exit as soon as any triangle is found to containthe point. This algorithm can be enhanced by both sorting the edges of eachtriangle by length and also sorting the testing order of triangles by theirareas. Larger triangles are more likely to enclose a point and so end testingearlier. Using both of these sorting strategies makes convex testing 1.2times faster for squares and 2.5 times faster for regular 100 sided polygons.

Another strategy is to test the point against each exterior edge in turn. Ifthe point is outside any edge, then the point must be outside the entireconvex polygon. This algorithm uses less additional storage than the trianglefan and is very simple to code.

The order of edges tested affects the speed of the algorithm; testing edgeswhich cut off the most area of the bounding box earliest on is the bestordering. Finding this optimal ordering is non-trivial, but doing the edgesin order is often the worst strategy, since each neighboring edge usually cutsoff little more area than the previous. Randomizing the order of the edgesmakes this algorithm up to 10% faster overall for regular polygons. However,even then the triangle fan algorithm with sorting is up to 1.35 times fasterfor 100 edge regular polygons.

The exterior edge strategy looks for an early exit due to the point beingoutside the polygon, while the triangle fan convex test looks for one due tothe point being inside. For example, for 100 edge polygons if all pointstested are inside the polygon the triangle fan is 1.7 times faster; if allare outside the exterior test is more than 11 times faster (but only 3 timesfaster if the edges are not randomized). So when the polygon/bounding box areais low the exterior edge strategy might be best.

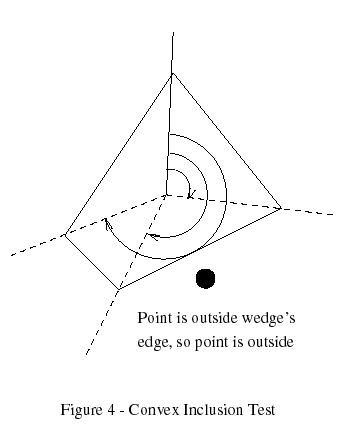
A method with O(log n) performance is discussed by Preparata and Shamos(Preparata 1985). The polygon is preprocessed by adding a central point to it and isthen divided into wedges. The angles from an anchor edge to each wedge'sedges are computed and saved, along with half-plane equations for each wedge'spolygon edge. When a point is tested, the angle from the anchor edge iscomputed and a binary search is used to determine the wedge it is in, then thecorresponding polygon edge is tested against it (Figure 4). This algorithm isslower for polygons with few edges because the startup cost is high, but thebinary search makes for a much faster test when the number of edges is high.

Edge Problems

A problem that is sometimes important is determining if a point is exactly onan edge of a polygon. Being "exactly" on an edge entails computing errorbounds and other issues in numerical analysis. While the "on" condition is ofinterest in CAD and elsewhere, for most computer graphics related operationsthis type of classification is unnecessary.

Problems occur in triangle fan algorithms when the code assumes that a pointthat lies on a triangle edge is inside that triangle. Points on the edgesbetween test triangles will be classified as being inside two triangles, andso will be classified as being outside the polygon. This problem does nothappen with the convex test. However, another problem is common to thisfamily of algorithms. If a point is on the edge between two polygons, it willbe classified as being inside both.

The code presented for these algorithms does not fully address either of theseproblems. In reality, a random point tested against a polygon using eitheralgorithm has an infinitesimal chance of landing exactly on any edge. Forrendering purposes this problem can be ignored, with the result being onemis-shaded pixel once in a great while.

The crossings test does not have these problems when the 2D polygons are inthe same plane. By the nature of the test, all points are consistentlycategorized as being to one side of any given edge or vertex. This means thatwhen a point is somewhere inside a mesh of polygons the point will always bein only one polygon. Points exactly on the unshared edge of a polygon will beclassified as arbitrarily inside or outside the polygon by this method,however. Again, this problem is rarely encountered in rendering and so canusually be ignored.

Faster Tests

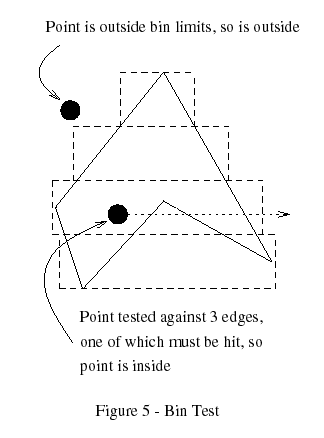
The algorithms presented so far for the general problem have been O(n); theorder of the problem is related to the number of edges. Preparata and Shamos(Preparata 1985) present a fascinating array of solutions which are theoreticallyfaster. However, these algorithms have various limitations and tend to bogdown when actually coded due to expensive operations. In this section aresome practical methods inspired by their presentation that perform well underordinary circumstances. They are still O(n) for pathological cases, but forreasonable polygon data they are quite efficient. These methods use much morememory and have higher initialization times before testing begins, but aremuch faster per tested point.

Bins Method

One method to speed up testing is to classify the edges by their Y componentsand then test only those edges with a chance of intersecting the test point'sX+ test ray. The bounding box surrounding the polygon is split into a numberof horizontal bins and the parts of the edges in a bin are kept in a list,sorted by the minimum X component. The maximum X of the edge is also saved,along with a flag noting whether the edge fully crosses the bin's Y bounds.In addition, the minimum and maximum X components of all the edges in each binare recorded.

When a point is to be classified, the proper bin is retrieved and if the pointis outside the X bounds, it must be outside the polygon. Else, the list istraversed and the edges tested against the point. Essentially, a modifiedcrossings test is done, with additional speed coming from the sorted order andfrom the storage of the "fully crosses" condition (Figure 5).

Grid Method

An even faster, and more memory intensive, method of testing for points insidea polygon is using lookup grids. The idea is to impose a grid inside thebounding box containing the polygon. Each grid cell is categorized as beingfully inside, fully outside, or indeterminate. The indeterminate cells alsohave a list of edges which overlap the cell, and also one corner (or more) isdetermined to be inside or outside using a traditional test. It is quick todetermine the state of these corners by dealing with those on each latitudeline by flipping the state of each corner to the right of the edge's crossingpoint.

To test a point against this structure is extremely quick in most cases. Fora reasonable polygon many of the cells are either inside or outside, sotesting consists of a simple look-up. If the cell contains edges, then a linesegment is formed from the test point to the cell corner and is tested againstall edges in the list (Antonio 1992). Since the state of the corner is known,the state of the test point can be found from the number of intersections(Figure 6).

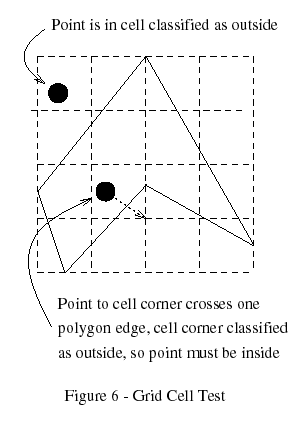
Care must be taken when a polygon edge exactly (or even nearly exactly)crosses a grid corner, as this corner is then unclassifiable. Rather thancoping with the topological and numerical problems involved, one simplesolution is to just start generating the grid from scratch again, givingslightly different dimensions to the bounding box. When testing the linesegment against the edges in a list, exact intersections of an edge endpointmust be counted only once.

One additional speed up is possible. Each grid cell has four sides. If noedges cross a side, then that side will be fully inside or outside thepolygon. A perfectly horizontal or vertical test line segment can then begenerated and the faster crossings test can be used against the edges in thecell. The only test case where this made a significant difference was witha 20x20 grid imposed on a 1000 edge polygon, where the grid cell side testwas 1.3 times faster.

Pixel Based Testing

One interesting case that is related to gridding is that of pixel-limitedpicking. When a dataset is displayed on the screen and a large amount ofpicking is to be done on a still image, a specialized test is worthwhile.Hanrahan and Haeberli(Hanrahan 1990) note that the image can be generated once into aseparate buffer, filling in each polygon's area with an identifying index.When a pixel is picked on this fixed image, the point is looked up in thisbuffer and the polygon selected is known immediately.

Statistics

The following timings were produced on an HP 720 RISC workstation; timings hadsimilar performance ratios on an IBM PC 386 with no FPU. The generalnon-convex algorithms were tested using two sorts of polygons: thosegenerated with random points and regular (i.e. equal length sides and vertexangles) polygons with a random rotation applied. Random polygons tend to besomewhat unlikely (no one ever uses 1000 edge random polygons for anythingexcept testing), while regular polygons are more orderly than a "typical"polygon; normal behavior tends to be somewhere in between. Convex-onlyalgorithms were tested with only regular polygons, and so have a certain biasto them. Test points were generated inside the box bounding the polygon.Timings are in microseconds per test, and appear to be within roughly +-10%accuracy. However, the best way to get true timings is to run the code onthe target machine; the code provided on disk has a test program which can beused to generate timings under various test conditions.

The performance of all the algorithms is practically linear; as such, theratios of times for the 1000 edge polygons are representative of performancefor polygons with a large number of edges.

General Algorithms, Random Polygons:

                       number of edges per polygon                         3       4      10      100    1000MacMartin               2.9     3.2     5.9     50.6    485Crossings               3.1     3.4     6.8     60.0    624Triangle Fan+edge sort  1.1     1.8     6.5     77.6    787Triangle Fan            1.2     2.1     7.3     85.4    865Barycentric             2.1     3.8    13.8    160.7   1665Angle Summation        56.2    70.4   153.6   1403.8  14693Grid (100x100)          1.5     1.5     1.6      2.1      9.8Grid (20x20)            1.7     1.7     1.9      5.7     42.2Bins (100)              1.8     1.9     2.7     15.1    117Bins (20)               2.1     2.2     3.7     26.3    278

General Algorithms, Regular Polygons:

                       number of edges per polygon                         3       4      10      100    1000MacMartin               2.7     2.8     4.0     23.7    225Crossings               2.8     3.1     5.3     42.3    444Triangle Fan+edge sort  1.3     1.9     5.2     53.1    546Triangle Fan            1.3     2.2     7.5     86.7    894Barycentric             2.1     3.9    13.0    143.5   1482Angle Summation        52.9    68.1   158.8   1489.3  15762Grid (100x100)          1.5     1.5     1.5      1.5      1.5Grid (20x20)            1.6     1.6     1.6      1.7      2.5Bins (100)              2.1     2.2     2.6      4.6      3.8Bins (20)               2.4     2.5     3.4      9.3     55.0

Convex Algorithms, Regular Polygons:

                       number of edges per polygon                         3       4      10      100    1000Inclusion               4.82    5.01    6.21     7.12     8.3Sorted Triangle Fan     1.11    1.41    3.75    29.36   289.6Unsorted Triangle Fan   1.25    2.04    6.30    69.18   734.7Unsorted Barycentric*   1.79    2.80    6.94    65.62   668.7Random Exterior Edges   1.11    1.61    3.82    33.44   333.6Ordered Exterior Edges  1.28    1.70    4.15    41.07   408.9Convex MacMartin        2.44    2.48    3.18    17.31   159.8

* The "unsorted barycentric" code is a slightly optimized version of Badouel'scode inGraphics Gems (Badoeul 1990).

Summary

The statistics vary depending on the machine and implementation, but thegeneral trends seem to hold. Avoid the angle summation test like the plague.For a general algorithm there are a few choices. Though it involvespreprocessing and additional storage, the triangle fan test with edges sortedby length is the best for polygons with few edges. The barycentric testworth using for triangles and for when these additional coordinates areneeded. The MacMartin test needs no additional memory or preprocessing and isgood for polygons with a fair number of edges (the break point was around 7 to9 edges vs. the triangle fan test on the HP 720) as is faster than thebarycentric test for all but triangles.

Of the algorithms with efficiency structures, the trapezoid algorithm issomewhere in between the edge based algorithms and the gridding algorithm inspeed. Gridding gives almost constant time performance for most normalpolygons, though like the other crossings test it performs a bit slower whenentirely random polygons are tested. Interestingly, even for polygons withjust a few edges the gridding algorithm outperforms most of the other tests.

Testing times can be noticeably decreased by using an algorithm optimized forconvex testing when possible. For example, the convex sorted triangle fantest is up to 2 times faster than its general case counterpart. For convexpolygons with many edges the inclusion test is extremely efficient because ofits O(log n) behavior. There is a zone from around 8 to 25 or so edges wherethe convex MacMartin test is slightly faster than the others, though notsignificantly so.

In summary, the basic crossings test is generally useful, but we can do better.Testing triangles using the sorted half-plane algorithm was more than twiceas fast; on the other end of the spectrum, the MacMartin optimization madetesting nearly twice as fast for polygons with many edges.

Code for this article is on the web.

from:http://erich.realtimerendering.com/ptinpoly/