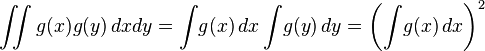机器学习：核函数的一个小题目

题目：给一百万个三角形，再给一个点，判断在不在某个三角形内。

解法1：如果不一样大的三角形，考虑用RTree

解法2：如果是一样大的三角形，可以用核函数映射。使得二维空间线性不可分的情况变为三维或四维空间线性可分的。

既然提到核函数，首先要知道核函数是什么，怎么去用。

----------------------------------------------------------------------

（1）核函数

核函数指所谓径向基函数（Radial Basis Function 简称 RBF），就是某种沿径向对称的标量函数。 

通常定义为空间中任一点x到某一中心xc之间欧氏距离的单调函数 , 可记作 k（||x-xc||）， 其作用往往是局部的 , 即当x远离xc时函数取值很小。

根据模式识别理论，低维空间线性不可分的模式通过非线性映射到高维特征空间则可能实现线性可分，但是如果直接采用这种技术在高维空间进行分类或回归，则存在确定非线性映射函数的形式和参数、特征空间维数等问题，而最大的障碍则是在高维特征空间运算时存在的“维数灾难”。采用核函数技术可以有效地解决这样问题。

设x,z∈X,X属于R（n）空间,非线性函数Φ实现输入空间X到特征空间F的映射,其中F属于R（m）,n<<m。根据核函数技术有：

K(x,z) =<Φ(x),Φ(z) > (1)

其中：<, >为内积,K(x,z)为核函数。 定义了一个n维到n+K维的映射。

简化计算二次规划中间的一步内积计算。也即中间步骤有一步必须求得。然而定义核函数之后，不需要显式计算每一个、甚至不需要知道长什么样的情况下，直接求出的值来。

举个简单多项式核的例子：

我们现在考虑核函数，即“内积平方”。这里面是二维空间中的两个点。

这个核函数对应着一个二维空间到三维空间的映射，它的表达式是：

，// 即映射

  // 即核函数

这里省去了对没一个点的的计算。 //省去对映射的计算

知乎用户王赟根据这个映射给出了一个直观的坐标变换，见下图：

   

文鸿郴的解释：核函数和映射没有关系。核函数只是用来计算映射到高维空间之后的内积的一种简便方法。

但为什么这么多的认知中核函数是一种映射呢：

一来这两件事一般先后进行，所以常常被混为一谈。

二来就像前面所述，核函数让人们不需要知道映射长什么样，不需要知道怎么选取映射，就能够算出内积。

因此这常常被认作是一种implicit mapping。这是由Mercer Theorem保证的，即只要核函数满足一定条件，那么映射空间一定存在。

也可以说，核函数、内积、相似度这三个词是等价的。

具体计算方式：先映射，再写出优化问题，求解过程中用到内积，内积计算时用到核函数简化计算。

如何确定这个内积是否存在呢？有一个牛逼的定理说，只要kernel满足一些条件，就存在这样一个（唯一的）内积结构与之对应。下面是这个定理的具体内容。

----------------------------------------------------------------------

（2）核函数要满足一个必备条件——Mercer's Condition

Mercer定理：任何半正定的函数都可以作为核函数。所谓半正定的函数f(xi,xj)，是指拥有训练数据集合（x1,x2,...xn)，我们定义一个矩阵的元素aij = f(xi,xj)，这个矩阵式n*n的，如果这个矩阵是半正定的，那么f(xi,xj)就称为半正定的函数。

请注意，这个mercer定理不是核函数必要条件，只是一个充分条件，即还有不满足mercer定理的函数也可以是核函数。所谓半正定指的就是核矩阵K的特征值均为非负。

维基百科定义：

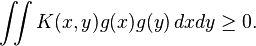
This is analogous to the idea of a positive-semidefinite matrix, which is a matrix M satisfying z^{T}Mz\geq0. The quantity z^{T}Mz can be thought of as a double sum, whereas the above integral is also analogous to a double sum.

例子，假设有一个常量函数

满足 Mercer's condition, 积分可以通过利用 Fubini's theorem 解释为：

且完全非负数，则这个函数满足核函数的条件。

知道了核函数的必备条件，记住一些常用核函数能省去不少功夫。

----------------------------------------------------------------------

（3）常用的核函数

线性核函数，多项式核函数，径向基核函数，Sigmoid核函数和复合核函数。

核函数的确定并不困难,满足Mercer定理的函数都可以作为核函数。

常用的核函数可分为两类，即内积核函数和平移不变核函数。现在设v1，v2为向量，则各个核函数表达式如下：

1) 线性核：                                          // 直接求内积

2) 多项式核：                   // 带参数、偏移、指数的内积

3) 径向基核：                  // 高斯核为典型（带参数）

4) Sigmoid核：        // 多项式核求双曲正切

以两个数为例：X=x, X=xi. 
 1）线性核函数K(x,xi) =x·xi；
 2）多项式核函数K(x,xi)=(x·xi+1)^d, d=1,2,…,N； 
 3）高斯核函数K(x,xi) =exp(-||x-xi||2/2σ2；
 4）感知器核函数K(x,xi) =tanh(βxi+b)；
 5）样条核函数K(x,xi) = B2n+1(x-xi)。

应用中最常见的是RBF核函数与Gaussian核函数，可以映射到无穷维。

核函数介绍完了，那么下面回到开头的问题上去。

----------------------------------------------------------------------

（4）开头给出三角形问题的个人思路

考虑二维到三维的映射。一百万个三角形，假设都是实心的。那么基本上覆盖了平面上的所有点。

采用类似的映射（还没想出来怎么构造）

映射到三维后，将所有三角形，映射到原点附近，一层一层叠起来，构成一个实心立方体（三棱柱）。

那么判断这个点是否在其中一个三角形内的问题，就变成了判断点是否在立方体内的问题。然而这个问题依然线性不可分。

继续高维映射，映射到四维空间，这个立方体被展开，那么问题就转变成判断这个点是否在平面一侧的分类问题。

如果这个面不是平面，而是曲面（对应不规则立方体），那么需要继续映射到五维，根据前述定理，总有一个维度使得这个问题线性可分。

欢迎留言讨论。