hdu1198 Farm Irrigation ----并查集

原题链接： http://acm.hdu.edu.cn/showproblem.php?pid=1198

一：原题内容

Problem Description

Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.


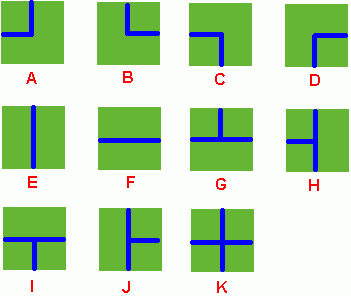
Figure 1

Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map

ADC
FJK
IHE

then the water pipes are distributed like


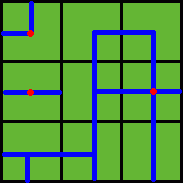
Figure 2

Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn.

Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him?

Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.

 

Input

There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.

 

Output

For each test case, output in one line the least number of wellsprings needed.

 

Sample Input

2 2DKHF3 3ADCFJKIHE-1 -1

Sample Output

23

二：分析理解

有如上图11种土地块，块中的绿色线条为土地块中修好的水渠，现在一片土地由上述的各种土地块组成，需要浇水，问需要打多少口井。能相连的地只需要打一口井。

容易想到并查集。只需要对每个地块与右方和下方的地块进行合并即可。合并之前先判断是否能连通，若能连通则合并，不能连通，则不能合并。能连通的时候就是正常的并查集了。

三：AC代码

#include<iostream>  #include<algorithm>  using namespace std;int type[11][4] = { { 1,1,0,0 },{ 0,1,1,0 },{ 1,0,0,1 },{ 0,0,1,1 },{ 0,1,0,1 },{ 1,0,1,0 },{ 1,1,1,0 },{ 1,1,0,1 },{ 1,0,1,1 },{ 0,1,1,1 },{ 1,1,1,1 }};int pre[55 * 55];char farm[55][55];int cnt;int m, n;int maxx;void init(int n){for (int i = 1; i <= 55*55; i++)pre[i] = i;cnt = n;}int find(int x){if (x == pre[x]) return x;pre[x] = find(pre[x]);return pre[x];}void join(int ax, int ay, int bx, int by, bool dir){if (bx > m || by > n) return;bool flag = false;//标识两块地是否可连int ta, tb;ta = farm[ax][ay] - 'A';tb = farm[bx][by] - 'A';if (dir)//竖直方向判断可连性{if (type[ta][3] && type[tb][1])flag = true;}else//水平方向判断可连性{if (type[ta][2] && type[tb][0])flag = true;}if (flag){int root_a = find(ax*maxx + ay);int root_b = find(bx*maxx + by);if (root_a != root_b){pre[root_a] = root_b;cnt--;}}}int main(){while (~scanf("%d%d", &m, &n) && (m > 0 && n > 0)){init(m*n);maxx = max(m, n) + 1;for (int i = 1; i <= m; i++)scanf("%s", farm[i] + 1);for (int i = 1; i <= m; i++){for (int j = 1; j <= n; j++){join(i, j, i + 1, j, true);join(i, j, i, j + 1, false);}}printf("%d\n", cnt);}return 0;}