最小二乘法

来源：互联网发布：java socket 发送编辑：程序博客网时间：2024/06/02 00:11

概念

最小二乘法多项式曲线拟合，根据给定的m个点,并不要求这条曲线精确地经过这些点，而是曲线y=f(x)的近似曲线y= φ(x)。

原理

[原理部分由个人根据互联网上的资料进行总结，希望对大家能有用]

给定数据点pi(xi,yi)，其中i=1,2,…,m。求近似曲线y= φ(x)。并且使得近似曲线与y=f(x)的偏差最小。近似曲线在点pi处的偏差δi= φ(xi)-y，i=1,2,...,m。

常见的曲线拟合方法:

1.使偏差绝对值之和最小

2.使偏差绝对值最大的最小

3.使偏差平方和最小

按偏差平方和最小的原则选取拟合曲线，并且采取二项式方程为拟合曲线的方法,称为最小二乘法。

推导过程：

1. 设拟合多项式为：

2. 各点到这条曲线的距离之和，即偏差平方和如下：

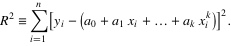
3. 为了求得符合条件的a值，对等式右边求ai偏导数，因而我们得到了：

.......

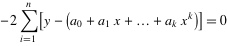
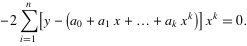
4. 将等式左边进行一下化简，然后应该可以得到下面的等式：

.......

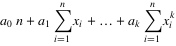
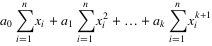
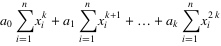
5. 把这些等式表示成矩阵的形式，就可以得到下面的矩阵：

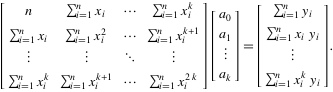
6. 将这个范德蒙得矩阵化简后可得到:

7. 也就是说X*A=Y，那么A = (X'*X)-1*X'*Y，便得到了系数矩阵A，同时，我们也就得到了拟合曲线。

实现

运行前提:

Python运行环境与编辑环境；
Matplotlib.pyplot图形库，可用于快速绘制2D图表，与matlab中的plot命令类似，而且用法也基本相同。

代码:

[python] view plain copy
# coding=utf-8  
  
''''' 
作者:Jairus Chan 
程序:多项式曲线拟合算法 
'''  
import matplotlib.pyplot as plt  
import math  
import numpy  
import random  
  
fig = plt.figure()  
ax = fig.add_subplot(111)  
  
#阶数为9阶  
order=9  
  
#生成曲线上的各个点  
x = numpy.arange(-1,1,0.02)  
y = [((a*a-1)*(a*a-1)*(a*a-1)+0.5)*numpy.sin(a*2) for a in x]  
#ax.plot(x,y,color='r',linestyle='-',marker='')  
#,label="(a*a-1)*(a*a-1)*(a*a-1)+0.5"  
  
#生成的曲线上的各个点偏移一下，并放入到xa,ya中去  
i=0  
xa=[]  
ya=[]  
for xx in x:  
    yy=y[i]  
    d=float(random.randint(60,140))/100  
    #ax.plot([xx*d],[yy*d],color='m',linestyle='',marker='.')  
    i+=1  
    xa.append(xx*d)  
    ya.append(yy*d)  
  
'''''for i in range(0,5): 
    xx=float(random.randint(-100,100))/100 
    yy=float(random.randint(-60,60))/100 
    xa.append(xx) 
    ya.append(yy)'''  
  
ax.plot(xa,ya,color='m',linestyle='',marker='.')  
  
  
#进行曲线拟合  
matA=[]  
for i in range(0,order+1):  
    matA1=[]  
    for j in range(0,order+1):  
        tx=0.0  
        for k in range(0,len(xa)):  
            dx=1.0  
            for l in range(0,j+i):  
                dx=dx*xa[k]  
            tx+=dx  
        matA1.append(tx)  
    matA.append(matA1)  
  
#print(len(xa))  
#print(matA[0][0])  
matA=numpy.array(matA)  
  
matB=[]  
for i in range(0,order+1):  
    ty=0.0  
    for k in range(0,len(xa)):  
        dy=1.0  
        for l in range(0,i):  
            dy=dy*xa[k]  
        ty+=ya[k]*dy  
    matB.append(ty)  
   
matB=numpy.array(matB)  
  
matAA=numpy.linalg.solve(matA,matB)  
  
#画出拟合后的曲线  
#print(matAA)  
xxa= numpy.arange(-1,1.06,0.01)  
yya=[]  
for i in range(0,len(xxa)):  
    yy=0.0  
    for j in range(0,order+1):  
        dy=1.0  
        for k in range(0,j):  
            dy*=xxa[i]  
        dy*=matAA[j]  
        yy+=dy  
    yya.append(yy)  
ax.plot(xxa,yya,color='g',linestyle='-',marker='')  
  
ax.legend()  
plt.show()  

运行效果:

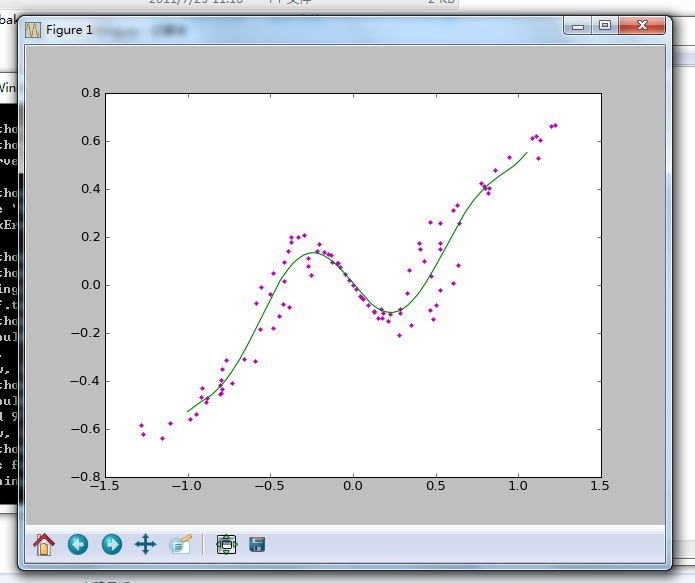
本博客中所有的博文都为笔者（Jairus Chan）原创。

如需转载，请标明出处：http://blog.csdn.net/JairusChan。

如果您对本文有任何的意见与建议，请联系笔者（JairusChan）。

一.背景

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

通过这段描述可以看出来，最小二乘法也是一种优化方法，求得目标函数的最优值。并且也可以用于曲线拟合，来解决回归问题。难怪《统计学习方法》中提到，回归学习最常用的损失函数是平方损失函数，在此情况下，回归问题可以著名的最小二乘法来解决。看来最小二乘法果然是机器学习领域做有名和有效的算法之一。

二. 最小二乘法

我们以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢？监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面...

对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：

        （1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
        （2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
        （3）最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。

　最常用的是普通最小二乘法（ Ordinary Least Square，OLS）：所选择的回归模型应该使所有观察值的残差平方和达到最小。（Q为残差平方和）- 即采用平方损失函数。

　样本回归模型：

其中e_i为样本（X_i,Y_i）的误差

平方损失函数：

则通过Q最小确定这条直线，即确定，以为变量，把它们看作是Q的函数，就变成了一个求极值的问题，可以通过求导数得到。求Q对两个待估参数的偏导数（偏导数存在）：

根据数学知识我们知道，函数的极值点为偏导为0的点。

解得：

这就是最小二乘法的解法，就是求得平方损失函数的极值点。

四. 最小二乘法与梯度下降法

最小二乘法跟梯度下降法都是通过求导来求损失函数的最小值，那它们有什么区别呢。

相同

　　1.本质相同：两种方法都是在给定已知数据（independent & dependent variables）的前提下对dependent variables算出出一个一般性的估值函数。然后对给定新数据的dependent variables进行估算。
　　2.目标相同：都是在已知数据的框架内，使得估算值与实际值的总平方差尽量更小（事实上未必一定要使用平方）

不同
　　1.实现方法和结果不同：最小二乘法是直接对 $\Delta$ 求导找出全局最小，是非迭代法。而梯度下降法是一种迭代法，先给定一个 $\beta$ ，然后向 $\Delta$ 下降最快的方向调整 $\beta$ ，在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢，并且对初始点的选择极为敏感，其改进大多是在这两方面下功夫。

逻辑回归logicalistic regression 本质上仍为线性回归，为什么被单独列为一类？

其存在一个非线性的映射关系，处理的一般是二元结构的0，1问题，是线性回归的扩展，应用广泛，被单独列为一类。

线性回归的损失函数是平方函数，而逻辑回归的损失函数是对数函数。

原文：http://www.cnblogs.com/iamccme/archive/2013/05/15/3080737.html

0 0