哈夫曼树

 一、哈夫曼树的概念和定义

 

什么是哈夫曼树？

让我们先举一个例子。

判定树：

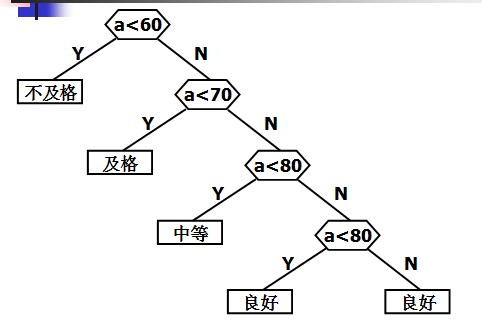
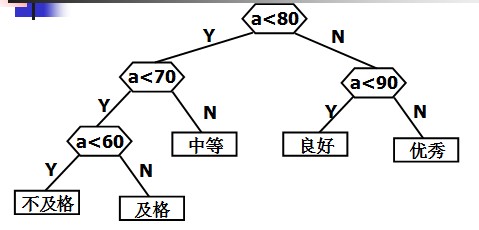
        在很多问题的处理过程中，需要进行大量的条件判断，这些判断结构的设计直接影响着程序的执行效率。例如，编制一个程序，将百分制转换成五个等级输出。大家可能认为这个程序很简单，并且很快就可以用下列形式编写出来：

        if(score<60)cout<<"Bad"<<endl;else if(score<70)cout<<"Pass"<<endlelse if(score<80)cout<<"General"<<endl;else if(score<90)cout<<"Good"<<endl;elsecout<<"Very good!"<<endl;</span>

若考虑上述程序所耗费的时间，就会发现该程序的缺陷。在实际中，学生成绩在五个等级上的分布是不均匀的。当学生百分制成绩的录入量很大时，上述判定过程需要反复调用，此时程序的执行效率将成为一个严重问题。

 

但在实际应用中，往往各个分数段的分布并不是均匀的。下面就是在一次考试中某门课程的各分数段的分布情况： 

 

 

下面我们就利用哈夫曼树寻找一棵最佳判定树，即总的比较次数最少的判定树。

 

 

第一种构造方式：

 

 

 

第二种构造方式：

 

 

 

 

这两种方式，显然后者的判定过程的效率要比前者高。在也没有别地判定过程比第二种方式的效率更高。

 

我们称判定过程最优的二叉树为哈夫曼树，又称最优二叉树

 

 

===================================================================================================

 

 定义哈夫曼树之前先说明几个与哈夫曼树有关的概念：

 

路径： 树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。

 

路径长度：路径上的分枝数目称作路径长度。

 

树的路径长度：从树根到每一个结点的路径长度之和。

 

结点的带权路径长度：在一棵树中，如果其结点上附带有一个权值，通常把该结点的路径长度与该结点上的权值

                                                              之积称为该结点的带权路径长度（weighted path length）

  什么是权值?( From 百度百科 )

    　计算机领域中（数据结构）

　　权值就是定义的路径上面的值。可以这样理解为节点间的距离。通常指字符对应的二进制编码出现的概率。

　　至于霍夫曼树中的权值可以理解为：权值大表明出现概率大！

　　一个结点的权值实际上就是这个结点子树在整个树中所占的比例.

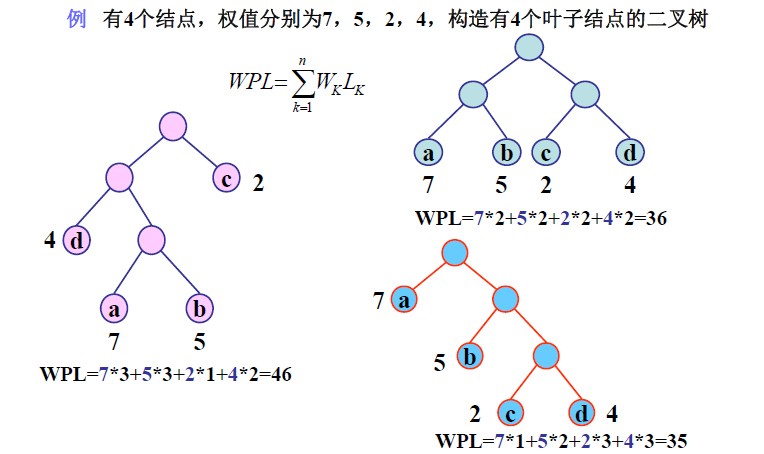
　　abcd四个叶子结点的权值为7,5,2,4. 这个7,5,2,4是根据实际情况得到的,比如说从一段文本中统计出abcd四个字母出现的次数分别为7,5,2,4. 说a结点的权值为7,意思是说a结点在系统中占有7这个份量.实际上也可以化为百分比来表示,但反而麻烦,实际上是一样的.

 

树的带权路径长度：如果树中每个叶子上都带有一个权值，则把树中所有叶子的带权路径长度之和称为树的带

                                   权路径长度。

             设某二叉树有n个带权值的叶子结点，则该二叉树的带权路径长度记为：

                                  

公式中，Wk为第k个叶子结点的权值；Lk为该结点的路径长度。

 

示例：

======================================================================================================

 

一般来说，用n（n>0）个带权值的叶子来构造二叉树，限定二叉树中除了这n个叶子外只能出现度为2的结点。

 

那么符合这样条件的二叉树往往可构造出许多颗，

 

 

其中带权路径长度最小的二叉树就称为哈夫曼树或最优二叉树

 

  二、哈夫曼树的构造

 

根据哈弗曼树的定义，一棵二叉树要使其WPL值最小，必须使权值越大的叶子结点越靠近根结点，而权值越小的叶子结点

越远离根结点。

 

哈弗曼依据这一特点提出了一种构造最优二叉树的方法，其基本思想如下：

 

下面演示了用Huffman算法构造一棵Huffman树的过程：

 

 

 

三、哈夫曼树的在编码中的应用

 

在电文传输中，需要将电文中出现的每个字符进行二进制编码。在设计编码时需要遵守两个原则：

（1）发送方传输的二进制编码，到接收方解码后必须具有唯一性，即解码结果与发送方发送的电文完全一样；

（2）发送的二进制编码尽可能地短。下面我们介绍两种编码的方式。

 

1. 等长编码

            这种编码方式的特点是每个字符的编码长度相同（编码长度就是每个编码所含的二进制位数）。假设字符集只含有4个字符A，B，C，D，用二进制两位表示的编码分别为00，01，10，11。若现在有一段电文为：ABACCDA，则应发送二进制序列：00010010101100，总长度为14位。当接收方接收到这段电文后，将按两位一段进行译码。这种编码的特点是译码简单且具有唯一性，但编码长度并不是最短的。

 

2. 不等长编码

            在传送电文时，为了使其二进制位数尽可能地少，可以将每个字符的编码设计为不等长的，使用频度较高的字符分配一个相对比较短的编码，使用频度较低的字符分配一个比较长的编码。例如，可以为A，B，C，D四个字符分别分配0，00，1，01，并可将上述电文用二进制序列：000011010发送，其长度只有9个二进制位，但随之带来了一个问题，接收方接到这段电文后无法进行译码，因为无法断定前面4个0是4个A，1个B、2个A，还是2个B，即译码不唯一，因此这种编码方法不可使用。

 

因此，为了设计长短不等的编码，以便减少电文的总长，还必须考虑编码的唯一性，即在建立不等长编码时必须使任何一个字符的编码都不是另一个字符的前缀，这宗编码称为前缀编码（prefix  code）

 

 

 

（1）利用字符集中每个字符的使用频率作为权值构造一个哈夫曼树；

（2）从根结点开始，为到每个叶子结点路径上的左分支赋予0，右分支赋予1，并从根到叶子方向形成该叶子结点的编码

 

 

例题：

假设一个文本文件TFile中只包含7个字符{A，B，C，D，E，F，G}，这7个字符在文本中出现的次数为{5，24，7，17，34，5，13}

利用哈夫曼树可以为文件TFile构造出符合前缀编码要求的不等长编码

 

具体做法：

 

1. 将TFile中7个字符都作为叶子结点，每个字符出现次数作为该叶子结点的权值

2. 规定哈夫曼树中所有左分支表示字符0，所有右分支表示字符1,将依次从根结点到每个叶子结点所经过的分支的二进制位的序列作为该

     结点对应的字符编码

3. 由于从根结点到任何一个叶子结点都不可能经过其他叶子，这种编码一定是前缀编码，哈夫曼树的带权路径长度正好是文件TFile编码

    的总长度

 

通过哈夫曼树来构造的编码称为哈弗曼编码（huffman code）

 

 

 

 

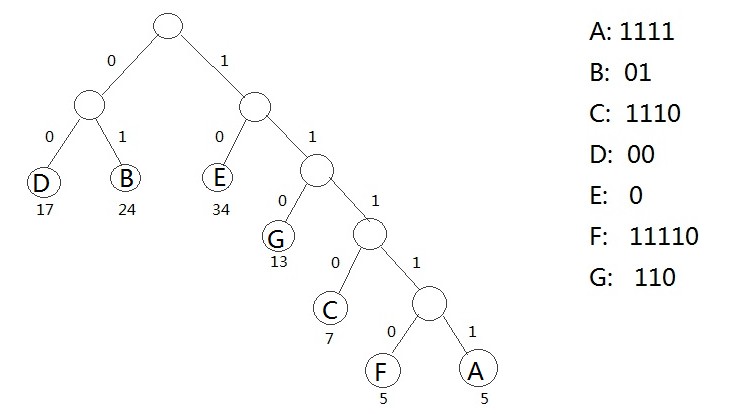
三、哈夫曼编码步骤

1、对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F= {T1,T2,T3,...,Ti,...,Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。（为方便在计算机上实现算 法，一般还要求以Ti的权值Wi的升序排列。）

2、在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。

3、从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。

4、重复2和3两步，直到集合F中只有一棵二叉树为止。

简易的理解就是，假如我有A,B,C,D,E五个字符，出现的频率（即权值）分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树，即取1，2构成新树，其结点为1+2=3，如图：

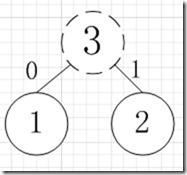
虚线为新生成的结点，第二步再把新生成的权值为3的结点放到剩下的集合中，所以集合变成{5,4,3,3}，再根据第二步，取最小的两个权值构成新树，如图：

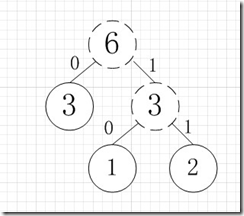
再依次建立哈夫曼树，如下图：

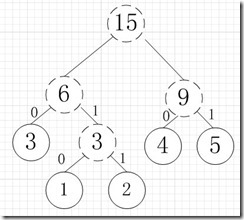
其中各个权值替换对应的字符即为下图：

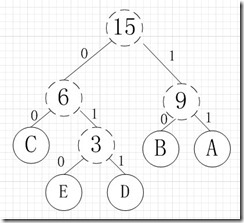
所以各字符对应的编码为：A->11,B->10,C->00,D->011,E->010

霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩，加密解密等场合。

 

#include <iostream>#include <stdlib.h>using namespace std;const int MaxValue = 10000;//初始设定的权值最大值const int MaxBit = 4;//初始设定的最大编码位数const int MaxN = 10;//初始设定的最大结点个数struct HaffNode//哈夫曼树的结点结构{    int weight;//权值    int flag;//标记    int parent;//双亲结点下标    int leftChild;//左孩子下标    int rightChild;//右孩子下标};struct Code//存放哈夫曼编码的数据元素结构{    int bit[MaxBit];//数组    int start;//编码的起始下标    int weight;//字符的权值};void Haffman(int weight[], int n, HaffNode haffTree[])//建立叶结点个数为n权值为weight的哈夫曼树haffTree{    int j, m1, m2, x1, x2;    //哈夫曼树haffTree初始化。n个叶结点的哈夫曼树共有2n-1个结点    for (int i = 0; i<2 * n - 1; i++)    {        if (i<n)            haffTree[i].weight = weight[i];        else            haffTree[i].weight = 0;        //注意这里没打else那{}，故无论是n个叶子节点还是n-1个非叶子节点都会进行下面4步的初始化        haffTree[i].parent = 0;        haffTree[i].flag = 0;        haffTree[i].leftChild = -1;        haffTree[i].rightChild = -1;    }    //构造哈夫曼树haffTree的n-1个非叶结点    for (int i = 0; i<n - 1; i++)    {        m1 = m2 = MaxValue;//Maxvalue=10000;(就是一个相当大的数)        x1 = x2 = 0;//x1、x2是用来保存最小的两个值在数组对应的下标         for (j = 0; j<n + i; j++)//循环找出所有权重中，最小的二个值--morgan        {            if (haffTree[j].weight<m1&&haffTree[j].flag == 0)            {                m2 = m1;                x2 = x1;                m1 = haffTree[j].weight;                x1 = j;            }            else if(haffTree[j].weight<m2&&haffTree[j].flag == 0)            {                m2 = haffTree[j].weight;                x2 = j;            }        }        //将找出的两棵权值最小的子树合并为一棵子树        haffTree[x1].parent = n + i;        haffTree[x2].parent = n + i;        haffTree[x1].flag = 1;        haffTree[x2].flag = 1;        haffTree[n + i].weight = haffTree[x1].weight + haffTree[x2].weight;        haffTree[n + i].leftChild = x1;        haffTree[n + i].rightChild = x2;    }}void HaffmanCode(HaffNode haffTree[], int n, Code haffCode[])//由n个结点的哈夫曼树haffTree构造哈夫曼编码haffCode{    Code *cd = new Code;    int child, parent;    //求n个叶结点的哈夫曼编码    for (int i = 0; i<n; i++)    {        //cd->start=n-1;//不等长编码的最后一位为n-1,        cd->start = 0;//,----修改从0开始计数--morgan        cd->weight = haffTree[i].weight;//取得编码对应权值的字符        child = i;        parent = haffTree[child].parent;        //由叶结点向上直到根结点        while (parent != 0)        {            if (haffTree[parent].leftChild == child)                cd->bit[cd->start] = 0;//左孩子结点编码0            else                cd->bit[cd->start] = 1;//右孩子结点编码1                                      //cd->start--;            cd->start++;//改成编码自增--morgan            child = parent;            parent = haffTree[child].parent;        }        //保存叶结点的编码和不等长编码的起始位        //for(intj=cd->start+1;j<n;j++)        for (int j = cd->start - 1; j >= 0; j--)//重新修改编码，从根节点开始计数--morgan            haffCode[i].bit[cd->start - j - 1] = cd->bit[j];         haffCode[i].start = cd->start;        haffCode[i].weight = cd->weight;//保存编码对应的权值    }}int main(){    int i, j, n = 4, m = 0;    int weight[] = { 2,4,5,7 };    HaffNode*myHaffTree = new HaffNode[2 * n - 1];    Code*myHaffCode = new Code[n];    if (n>MaxN)    {        cout << "定义的n越界，修改MaxN!" << endl;        exit(0);    }    Haffman(weight, n, myHaffTree);    HaffmanCode(myHaffTree, n, myHaffCode);    //输出每个叶结点的哈夫曼编码    for (i = 0; i<n; i++)    {        cout << "Weight=" << myHaffCode[i].weight << "  Code=";        //for(j=myHaffCode[i].start+1;j<n;j++)        for (j = 0; j<myHaffCode[i].start; j++)            cout << myHaffCode[i].bit[j];        m = m + myHaffCode[i].weight*myHaffCode[i].start;        cout << endl;    }    cout << "huffman's WPL is:";    cout << m;    cout << endl;    return 0;}