POJ 3009 Curling 2.0

Curling 2.0

Time Limit: 1000MS Memory Limit: 65536KTotal Submissions: 18264 Accepted: 7517

Description

On Planet MM-21, after their Olympic games this year, curling is getting popular. But the rules are somewhat different from ours. The game is played on an ice game board on which a square mesh is marked. They use only a single stone. The purpose of the game is to lead the stone from the start to the goal with the minimum number of moves.

Fig. 1 shows an example of a game board. Some squares may be occupied with blocks. There are two special squares namely the start and the goal, which are not occupied with blocks. (These two squares are distinct.) Once the stone begins to move, it will proceed until it hits a block. In order to bring the stone to the goal, you may have to stop the stone by hitting it against a block, and throw again.

Fig. 1: Example of board (S: start, G: goal)

The movement of the stone obeys the following rules:

• At the beginning, the stone stands still at the start square.
• The movements of the stone are restricted to x and y directions. Diagonal moves are prohibited.
• When the stone stands still, you can make it moving by throwing it. You may throw it to any direction unless it is blocked immediately(Fig. 2(a)).
• Once thrown, the stone keeps moving to the same direction until one of the following occurs:
  • The stone hits a block (Fig. 2(b), (c)).
    • The stone stops at the square next to the block it hit.
    • The block disappears.
  • The stone gets out of the board.
    • The game ends in failure.
  • The stone reaches the goal square.
    • The stone stops there and the game ends in success.
• You cannot throw the stone more than 10 times in a game. If the stone does not reach the goal in 10 moves, the game ends in failure.

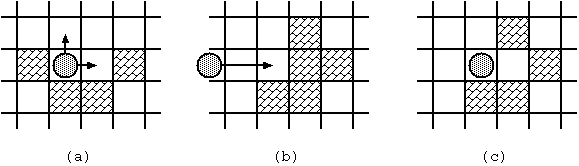
Fig. 2: Stone movements

Under the rules, we would like to know whether the stone at the start can reach the goal and, if yes, the minimum number of moves required.

With the initial configuration shown in Fig. 1, 4 moves are required to bring the stone from the start to the goal. The route is shown in Fig. 3(a). Notice when the stone reaches the goal, the board configuration has changed as in Fig. 3(b).

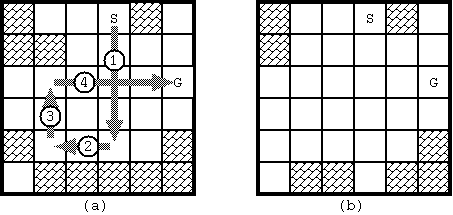
Fig. 3: The solution for Fig. D-1 and the final board configuration

Input

The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets never exceeds 100.

Each dataset is formatted as follows.

the width(=w) and the height(=h) of the board 
First row of the board 
... 
h-th row of the board

The width and the height of the board satisfy: 2 <= w <= 20, 1 <= h <= 20.

Each line consists of w decimal numbers delimited by a space. The number describes the status of the corresponding square.

0vacant square1block2start position3goal position

The dataset for Fig. D-1 is as follows:

6 6 
1 0 0 2 1 0 
1 1 0 0 0 0 
0 0 0 0 0 3 
0 0 0 0 0 0 
1 0 0 0 0 1 
0 1 1 1 1 1

Output

For each dataset, print a line having a decimal integer indicating the minimum number of moves along a route from the start to the goal. If there are no such routes, print -1 instead. Each line should not have any character other than this number.

Sample Input

2 13 26 61 0 0 2 1 01 1 0 0 0 00 0 0 0 0 30 0 0 0 0 01 0 0 0 0 10 1 1 1 1 16 11 1 2 1 1 36 11 0 2 1 1 312 12 0 1 1 1 1 1 1 1 1 1 313 12 0 1 1 1 1 1 1 1 1 1 1 3
0 0
**大意就是把球从起点推到终点，遇到 1 会停下来，并把前面的一个1撞碎，找最小步数
应为地图是动态的，所以广搜很不好实现，加上步数不超过10 ，用深搜加回溯是比较好的
注意几点
0. 1 是可以撞碎的
1.不要以为遇到边界可以停下， The stone gets out of the board.The game ends in failure. 出界就是 -1， 2.注意起点2的判断，又可以遇到起点而以为终止 3，注意在移动的过程中一旦经过终点会立刻停下来，而不一定是最后停在终点才算赢
 4，注意测试数据
6 11 1 2 1 1 36 11 0 2 1 1 3
如果下一个位置直接是墙或者出界，也是无法移动的 

#include <iostream>#include <algorithm>using namespace std;const int INF = 0x3f3f3f;int map[22][22];int go[4][2]={{1,0},{0,1},{-1,0},{0,-1}};//四个方向的移动 int start_x,start_y,goal_x,goal_y,w,h,themin;bool isok(int x,int y)//判断是否出界 {if(x<0 || x>=h || y<0 || y>=w)return false;else return true;}void dfs(int x,int y,int step){if(step>10)return ;if(map[x][y]==3)//到达了终点就取最小值，毕竟方法可能不为1 {themin = min(themin,step);}for(int i=0;i<4;i++){int px = x,py = y;//这里我是先判断再移动，有很多是先移动再判断的，仔细体会其中的差别 if(map[px+go[i][0]][py+go[i][1]]==1 || isok(px+go[i][0],py+go[i][1])==false)//如果下一个位置直接是墙或者出界，也算无法移动的 continue;else {while(map[px+go[i][0]][py+go[i][1]]!=1 && isok(px+go[i][0],py+go[i][1])==true){px += go[i][0],py += go[i][1];if(map[px][py]==3)//在移动过程中经过了终点，也算是胜利 themin = min(themin,step+1);}}if(map[px+go[i][0]][py+go[i][1]]==1) //下面就没什么可说的了 {map[px+go[i][0]][py+go[i][1]] = 0;dfs(px,py,step+1);map[px+go[i][0]][py+go[i][1]] = 1;}}}int main(){int i,j;while(cin>>w>>h&&w!=0&&h!=0){fill(map[0],map[0]+22*22,0);for(i=0;i<h;i++)for(j=0;j<w;j++){cin>>map[i][j];if(map[i][j]==2){start_x = i , start_y = j;map[i][j] = 0;}else if(map[i][j]==3)goal_x = i , goal_y = j;}themin = INF,isfind = false;dfs(start_x,start_y,0);if(themin<=10)cout<<themin<<endl;elsecout<<"-1"<<endl;}return 0;}


奈何我冒泡的算法如何打动你超时的心！！