tyvj模拟赛

算

【问题背景】

zhx帮他妹子做数学题。

【问题描述】

求：

如N=3, M=3，这个值为1^1+1^2+1^3+2^1+2^2+2^3+3^1+3^2+3^3=56。

【输入格式】

仅一行，包含两个数N和M.

【输出格式】

仅一行，包含所求的答案mod10^9 + 7的值。

【样例输入】

3 3

【样例输出】

56

【数据范围与规定】

对于的数据，所有。

对于的数据，所有。

游

【问题背景】

zhx和他的妹子出去玩。

【问题描述】

zhx和他的妹子去一个国家旅游，共有N个旅游景点，N-1条双向连接的道路将它们联通起来，每一条道路有固定长度。一开始zhx位于1号景点。

现在希望你能够求出旅行长度最小的方案，使得每个景点至少被访问到一次。

【输入格式】

第一行两个整数N，代表景点数目。

接下来N-1行，每行三个整数s, t, w，表示有一条从s到t的双向道路，长度为w。s和t的编号从1开始。

【输出格式】

一行一个整数，代表能够访问每个景点至少一次的方案的最小旅行长度。

【样例输入】

3

1 2 3

2 3 3

【样例输出】

6

【样例输入】

3

1 2 3

1 3 3

【样例输出】

9

【数据规模与约定】

对于的数据，。

对于的数据，。

对于的数据，，。

运

【问题背景】

zhx和妹子们玩数数游戏。

【问题描述】

仅包含4或7的数被称为幸运数。

一个序列的子序列被定义为从序列中删去若干个数，剩下的数组成的新序列。两个子序列被定义为不同的当且仅当其中的元素在原始序列中的下标的集合不相等。对于一个长度为N的序列，共有2^N个不同的子序列。（包含一个空序列）。

一个子序列被称为不幸运的，当且仅当其中不包含两个相同的幸运数。

对于一个给定序列，求其中长度恰好为K的不幸运子序列的个数，答案mod 10^9+7输出。

【输入格式】

第一行两个正整数N，K，表示原始序列的长度和题目中的K。

接下来一行N个整数a_i，表示序列中第i个元素的值。

【输出格式】

仅一个数，表示不幸运子序列的个数。（mod 10^9+7）

【样例输入】

3 2

1 1 1

【样例输出】

3

【样例输入】

4 2

4 7 4 7

【样例输出】

4

 

【样例解释】

对于样例1，每个长度为2的子序列都是符合条件的。

对于样例2，4个不幸运子序列元素下标分别为：{1, 2}, {3, 4}, {1, 4}, {2, 3}。注意下标集{1, 3}对应的子序列不是“不幸运”的，因为它包含两个相同的幸运数4.

【数据规模与约定】

对于的数据，  

对于的数据，  。

对于的数据，

tyvj就是不给我测！

这套 题真心挺好，难度还是很合适的，当然再难一点也是可以挑战一下的。

 

t1 等比数列求和搞一搞

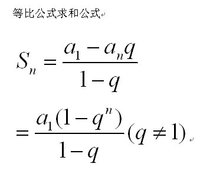
 有除法，逆元搞一搞。

 

 

#include<cstdio>#include<cstring>#include<cmath>#include<algorithm>using namespace std;typedef long long ll;const ll mod=1e9+7;ll n,m;void exgcd(ll a,ll b,ll &d,ll &x,ll &y){if (b==0) {d=a;x=1;y=0;return ;}exgcd(b,a%b,d,y,x);y-=x*(a/b);}ll ny(ll a,ll n){ll d,x,y;exgcd(a,n,d,x,y);return (x%n+n)%n;}ll power_mod(ll a,ll b){ll ans=1;while (b){if (b&1) ans=ans*a%mod;a=a*a%mod;b>>=1;}return ans;}int main(){freopen("sum.in","r",stdin);freopen("sum.out","w",stdout);scanf("%lld%lld",&n,&m);ll ans=m;for (ll i=2;i<=n;i++){ll tmp=0;tmp=((power_mod(i,m)*i%mod-i)%mod+mod)%mod;tmp=tmp*ny(i-1,mod)%mod;ans=(tmp+ans)%mod;}printf("%lld",ans);fclose(stdin);fclose(stdout);return 0;}

t2

从一号节点遍历遍历一棵树，停在一个节点，求最短路程。

和以前做的poj那一个题有相似之处，并且更简单了一点。

就是总长度*2-书上最长的节点距离，类似树形dp dfs 扫一遍就好。

#include<cstdio>#include<algorithm>#include<cstring>#include<cstdlib>using namespace std;const int N=50050;int n,m;int head[N],tot,fa[N],f[N],sum[N];struct aa{int to,pre,dis;}edge[N*2];void addedge(int x,int y,int z){edge[++tot].dis=z;edge[tot].to=y;edge[tot].pre=head[x];head[x]=tot;}void dfs(int u){for (int i=head[u];i;i=edge[i].pre)if (edge[i].to!=fa[u]){int v=edge[i].to;sum[v]=edge[i].dis*2;fa[v]=u;dfs(v);sum[u]+=sum[v];f[u]=max(f[v]+edge[i].dis,f[u]);}}int main(){freopen("tour.in","r",stdin);freopen("tour.out","w",stdout);scanf("%d",&n);int x,y,z;for (int i=1;i<n;i++){scanf("%d%d%d",&x,&y,&z);addedge(x,y,z);addedge(y,x,z);}dfs(1);printf("%d",sum[1]-f[1]);fclose(stdin);fclose(stdout);return 0;}

 

题3

这题比较影响人的思路的是，问不幸运的数列，不要条件反射的想求幸运的，相再减求幸运的。

 

首先，本题的幸运数最多只有一千多个吧，先把这些幸运数处理出来（每一位只有可能是4或7，每一位只有两种选择），
处理出每一个幸运数的个数。
对于不是幸运数的剩下d 个数来说，这就是一个组合问题了。因此总方案数为：（设幸运
数种数为tot，非幸运数个数为d）

ans=sgema （i） C（d，i） *dp【tot】【k-i】；
然后，对于这个calc 数组，显然是一个简单的dp 了。设dp[i][j]表示从前i 种幸运数
中取出j 个数的方案数。因为一种幸运数要么取一个要么不取，dp 方程即为：（C[i]表示
映射后的第i 种幸运数的个数）。
dp[i][j]=dp[i−1][j]+dp[i−1][j−1]∗ C[i]
初值即为
dp[i][0]=1(0<=i<=tot)
然后就解决了这个问题，复杂度O(n)左右。

 

#include<cstdio>#include<cstring>#include<cmath>#include<algorithm>#include<cstdlib>using namespace std;typedef long long ll;const ll mod=1e9+7;ll n,n1,n2,k;ll luck[20059],num,size[20095];ll f1[1200005],f[20055];void dfs(ll i,ll now){ if (now) luck[++num]=now; if (i==10) return ; dfs(i+1,now*10+4); dfs(i+1,now*10+7);}void init(){ dfs(1,0); sort(luck+1,luck+num+1);}void exgcd(ll a,ll b,ll &d,ll &x,ll &y){ if (b==0){d=a;x=1;y=0;return ;} exgcd(b,a%b,d,y,x);y-=x*(a/b);}ll ny(ll a,ll n){ ll x,y,d; exgcd(a,n,d,x,y); return (x%n+n)%n;}void work(ll *f,ll n){ f[0]=1; for (int i=0;i<n;i++) f[i+1]=f[i]*(n-i)%mod*ny(i+1,mod)%mod;}void work2(){ f[0]=1; for (int i=1;i<=num;i++) if (size[i]>=2) {  for (int j=num;j>=1;j--)  f[j]=(f[j-1]*size[i]%mod+f[j])%mod; }}int main(){ freopen("lucky.in","r",stdin); freopen("lucky.out","w",stdout); scanf("%lld%lld",&n,&k); init(); ll x; n1=n; for (int i=1;i<=n;i++) {  scanf("%lld",&x);  ll pos=lower_bound(luck+1,luck+num+1,x)-luck;  if (luck[pos]==x)   {   size[pos]++;   if (size[pos]==2)   {    n2++;    n1-=2;   }   if (size[pos]>2) n1--;  } }  work(f1,n1); work2();  ll ans=0; for (int i=0;i<=k;i++) {  ans=(f1[i]*f[k-i]%mod+ans)%mod; }  printf("%lld",ans); fclose(stdin); fclose(stdout); return 0;}

这道题在编写的时候，很巧妙的，通过数据大小分析题目语句分析，验证了思路的正确性，即那些约束恰好满足这道题目的算法。

感觉还是比较锻炼思维的，一步一步的推，很顺的。