codeforces 268D Wall Bars

Manao is working for a construction company. Recently, an order came to build wall bars in a children's park. Manao was commissioned to develop a plan of construction, which will enable the company to save the most money.

After reviewing the formal specifications for the wall bars, Manao discovered a number of controversial requirements and decided to treat them to the company's advantage. His resulting design can be described as follows:

• Let's introduce some unit of length. The construction center is a pole of height n.
• At heights 1, 2, ..., n exactly one horizontal bar sticks out from the pole. Each bar sticks in one of four pre-fixed directions.
• A child can move from one bar to another if the distance between them does not exceed h and they stick in the same direction. If a child is on the ground, he can climb onto any of the bars at height between 1 and h. In Manao's construction a child should be able to reach at least one of the bars at heights n - h + 1, n - h + 2, ..., n if he begins at the ground.

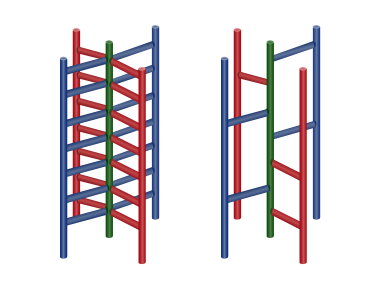The figure to the left shows what a common set of wall bars looks like. The figure to the right shows Manao's construction

Manao is wondering how many distinct construction designs that satisfy his requirements exist. As this number can be rather large, print the remainder after dividing it by 1000000009 (109 + 9). Two designs are considered distinct if there is such height i, that the bars on the height i in these designs don't stick out in the same direction.

Input

A single line contains two space-separated integers, n and h (1 ≤ n ≤ 1000, 1 ≤ h ≤ min(n, 30)).

Output

In a single line print the remainder after dividing the number of designs by 1000000009 (109 + 9).

Examples

input

5 1

output

4

input

4 2

output

148

input

4 3

output

256

input

5 2

output

376

Note

Consider several designs for h = 2. A design with the first bar sticked out in direction d1, the second — in direction d2 and so on (1 ≤ di ≤ 4) is denoted as string d1d2...dn.

Design "1231" (the first three bars are sticked out in different directions, the last one — in the same as first). A child can reach neither the bar at height 3 nor the bar at height 4.

Design "414141". A child can reach the bar at height 5. To do this, he should first climb at the first bar, then at the third and then at the fifth one. He can also reach bar at height 6 by the route second  →  fourth  →  sixth bars.

Design "123333". The child can't reach the upper two bars.

Design "323323". The bar at height 6 can be reached by the following route: first  →  third  →  fourth  →  sixth bars.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

魔性DP……第一次见到五维的动规……

因为四面是对称的，所以考虑时以一面为主要面（并不是说确定是哪一面，只是用来记录状态，具体看代码~），否则会重复。

f[i][a][b][c][d]表示高度为i，主要一面连续（1）与否（0），其余三面现有距离分别为b，c，d的种类数。

其余面超过h的话就直接记为h，反正已经没有影响，肯定不能作为主要面来计算了。（题目这里是不是有点问题？应该是小于h才能爬吧?）

具体的递推式见代码~看到神犇用了一个inc（int &u）函数来计算，让代码简化了很多，学习了~

一定要取模！！！

#include<cstdio>#define modd 1000000009int n,h,f[1001][2][33][33][33],val,ans;int inc(int &u){(u+=val)%=modd;}int main(){scanf("%d%d",&n,&h);f[0][0][0][0][0]=1;for(int i=1;i<=n;i++)  for(int a=0;a<=1;a++)    for(int b=0;b<=h;b++)      for(int c=0;c<=h;c++)        for(int d=0;d<=h;d++)          if(val=f[i-1][a][b][c][d])          {                inc(f[i][a<1 ? 0:1][b<h ? b+1:h][c<h ? c+1:h][d<h ? d+1:h]);            inc(f[i][b<h ? 0:1][c<h ? c+1:h][d<h ? d+1:h][a<1 ? a+1:h]);            inc(f[i][c<h ? 0:1][d<h ? d+1:h][a<1 ? a+1:h][b<h ? b+1:h]);            inc(f[i][d<h ? 0:1][a<1 ? a+1:h][b<h ? b+1:h][c<h ? c+1:h]);  }for(int a=0;a<=1;a++)  for(int b=0;b<=h;b++)    for(int c=0;c<=h;c++)      for(int d=0;d<=h;d++)        if((val=f[n][a][b][c][d]) && (a<1 || b<h || c<h || d<h)) inc(ans);printf("%d\n",ans);return 0;}