The Lost House--经典树形DP
来源:互联网 发布:python对电脑的要求 编辑:程序博客网 时间:2024/06/01 07:33
The Lost House
Time Limit: 3000MS Memory Limit: 30000KTotal Submissions: 2661 Accepted: 1129
Description
One day a snail climbed up to a big tree and finally came to the end of a branch. What a different feeling to look down from such a high place he had never been to before! However, he was very tired due to the long time of climbing, and fell asleep. An unbelievable thing happened when he woke up ---- he found himself lying in a meadow and his house originally on his back disappeared! Immediately he realized that he fell off the branch when he was sleeping! He was sure that his house must still be on the branch he had been sleeping on. The snail began to climb the tree again, since he could not live without his house.
When reaching the first fork of the tree, he sadly found that he could not remember the route that he climbed before. In order to find his lovely house, the snail decided to go to the end of every branch. It was dangerous to walk without the protection of the house, so he wished to search the tree in the best way.
Fortunately, there lived many warm-hearted worms in the tree that could accurately tell the snail whether he had ever passed their places or not before he fell off.
Now our job is to help the snail. We pay most of our attention to two parts of the tree ---- the forks of the branches and the ends of the branches, which we call them key points because key events always happen there, such as choosing a path, getting the help from a worm and arriving at the house he is searching for.
Assume all worms live at key points, and all the branches between two neighboring key points have the same distance of 1. The snail is now at the first fork of the tree.
Our purpose is to find a proper route along which he can find his house as soon as possible, through the analysis of the structure of the tree and the locations of the worms. The only restriction on the route is that he must not go down from a fork until he has reached all the ends grown from this fork.
The house may be left at the end of any branches in an equal probability. We focus on the mathematical expectation of the distance the snail has to cover before arriving his house. We wish the value to be as small as possible.
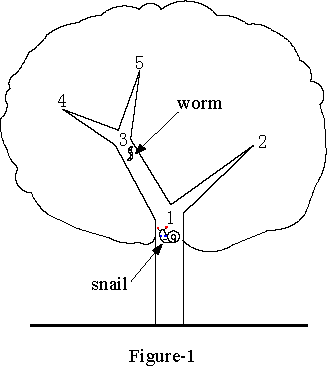
As illustrated in Figure-1, the snail is at the key point 1 and his house is at a certain point among 2, 4 and 5. A worm lives at point 3, who can tell the snail whether his house is at one of point 4 and 5 or not. Therefore, the snail can choose two strategies. He can go to point 2 first. If he cannot find the house there, he should go back to point 1, and then reaches point 4 (or 5) by point 3. If still not, he has to return point 3, then go to point 5 (or 4), where he will undoubtedly find his house. In this choice, the snail covers distances of 1, 4, 6 corresponding to the circumstances under which the house is located at point 2, 4 (or 5), 5 (or 4) respectively. So the expectation value is (1 + 4 + 6) / 3 = 11 / 3. Obviously, this strategy does not make full use of the information from the worm. If the snail goes to point 3 and gets useful information from the worm first, and then chooses to go back to point 1 then towards point 2, or go to point 4 or 5 to take his chance, the distances he covers will be 2, 3, 4 corresponding to the different locations of the house. In such a strategy, the mathematical expectation will be (2 + 3 + 4) / 3 = 3, and it is the very route along which the snail should search the tree.
When reaching the first fork of the tree, he sadly found that he could not remember the route that he climbed before. In order to find his lovely house, the snail decided to go to the end of every branch. It was dangerous to walk without the protection of the house, so he wished to search the tree in the best way.
Fortunately, there lived many warm-hearted worms in the tree that could accurately tell the snail whether he had ever passed their places or not before he fell off.
Now our job is to help the snail. We pay most of our attention to two parts of the tree ---- the forks of the branches and the ends of the branches, which we call them key points because key events always happen there, such as choosing a path, getting the help from a worm and arriving at the house he is searching for.
Assume all worms live at key points, and all the branches between two neighboring key points have the same distance of 1. The snail is now at the first fork of the tree.
Our purpose is to find a proper route along which he can find his house as soon as possible, through the analysis of the structure of the tree and the locations of the worms. The only restriction on the route is that he must not go down from a fork until he has reached all the ends grown from this fork.
The house may be left at the end of any branches in an equal probability. We focus on the mathematical expectation of the distance the snail has to cover before arriving his house. We wish the value to be as small as possible.
As illustrated in Figure-1, the snail is at the key point 1 and his house is at a certain point among 2, 4 and 5. A worm lives at point 3, who can tell the snail whether his house is at one of point 4 and 5 or not. Therefore, the snail can choose two strategies. He can go to point 2 first. If he cannot find the house there, he should go back to point 1, and then reaches point 4 (or 5) by point 3. If still not, he has to return point 3, then go to point 5 (or 4), where he will undoubtedly find his house. In this choice, the snail covers distances of 1, 4, 6 corresponding to the circumstances under which the house is located at point 2, 4 (or 5), 5 (or 4) respectively. So the expectation value is (1 + 4 + 6) / 3 = 11 / 3. Obviously, this strategy does not make full use of the information from the worm. If the snail goes to point 3 and gets useful information from the worm first, and then chooses to go back to point 1 then towards point 2, or go to point 4 or 5 to take his chance, the distances he covers will be 2, 3, 4 corresponding to the different locations of the house. In such a strategy, the mathematical expectation will be (2 + 3 + 4) / 3 = 3, and it is the very route along which the snail should search the tree.

Input
The input contains several sets of test data. Each set begins with a line containing one integer N, no more than 1000, which indicates the number of key points in the tree. Then follow N lines describing the N key points. For convenience, we number all the key points from 1 to N. The key point numbered with 1 is always the first fork of the tree. Other numbers may be any key points in the tree except the first fork. The i-th line in these N lines describes the key point with number i. Each line consists of one integer and one uppercase character 'Y' or 'N' separated by a single space, which represents the number of the previous key point and whether there lives a worm ('Y' means lives and 'N' means not). The previous key point means the neighboring key point in the shortest path between this key point and the key point numbered 1. In the above illustration, the previous key point of point 2 or 3 is point 1, while the previous key point of point 4 or 5 is point 3. This integer is -1 for the key point 1, means it has no previous key point. You can assume a fork has at most eight branches. The first set in the sample input describes the above illustration.
A test case of N = 0 indicates the end of input, and should not be processed.
A test case of N = 0 indicates the end of input, and should not be processed.
Output
Output one line for each set of input data. The line contains one float number with exactly four digits after the decimal point, which is the mathematical expectation value.
Sample Input
5-1 N1 N1 Y3 N3 N10-1 N1 Y1 N2 N2 N2 N3 N3 Y8 N8 N6-1 N1 N1 Y1 N3 N3 N0
Sample Output
3.00005.00003.5000题目链接:http://poj.org/problem?id=2057
好吧,我还是太渣了。
题目的意思是说有一个蜗牛在一棵树上睡觉,醒过来后发现从树上掉下来了,但是他的房子(壳)却落在了树上,他忘记了他在哪个树枝上睡觉了,现在他要去找到自己的屋子,树上有热心的毛毛虫会告诉他他有没有从这根树枝上滑下来,求蜗牛所爬步数的最小期望。
这个题我想了好久知道是个树形DP但是并没有什么思路,无奈我只能去搜了题解,就是题解我还理解了半天,我太菜了,还需要更努力啊,下面我放几个大牛的链接吧,大写的服啊,等过两天我再回来做一下这个题。
大牛的链接:
http://www.cnblogs.com/Lyush/archive/2013/01/16/2863399.html
http://blog.csdn.net/lin375691011/article/details/31446343
http://blog.csdn.net/winddreams/article/details/46980953
看了这三篇博客大概就知道这个题该怎么做了,要记得有退回的步数。
继续朝着大牛的不归路努力吧。
渣渣的代码:
#include <cstdio>#include <cstring>#include <iostream>#include <vector>#include <algorithm>using namespace std;struct node{ int u,v,w; int pre;}edge[1005];int p[1005],nEdge;int N;int dp[1005][2],ch[1005];int k[1005];void Init(){ memset(p,-1,sizeof(p)); memset(dp,0,sizeof(dp)); memset(ch,0,sizeof(ch)); nEdge=0;}void connect(int u,int v){ nEdge++; edge[nEdge].v=v; edge[nEdge].pre=p[u]; p[u]=nEdge;}bool cmp(int a,int b){ return (dp[a][0]+2)*ch[b]<(dp[b][0]+2)*ch[a];}int dfs(int x){ if(p[x]==-1){//说明是叶子节点 dp[x][1]=dp[x][0]=0; return ch[x]=1;//返回叶子节点的个数 } vector<int >v; for(int i=p[x];~i;i=edge[i].pre){ ch[x]+=dfs(edge[i].v); v.push_back(edge[i].v); } sort(v.begin(),v.end(),cmp); for(int i=0;i!=(int)v.size();i++){ dp[x][1]+=dp[x][0]*ch[v[i]]+dp[v[i]][1]+ch[v[i]]; dp[x][0]+=dp[v[i]][0]+2; } if(k[x]){//毛毛虫提醒过了 dp[x][0]=0; } return ch[x];}int main(){ int pre; char s[5]; while(~scanf("%d",&N)&&N){ Init(); scanf("%d %s",&pre,s);// for(int i=2;i<=N;i++){ scanf("%d%s",&pre,s); k[i]=s[0]=='Y'; connect(pre,i); } dfs(1);//一号节点是根节点 printf("%.4f\n",1.0*dp[1][1]/ch[1]); } return 0;}/*这里放上大牛的解题思路,留作存档,膜拜中。。。题意:有一只蜗牛爬上树睡着之后从树上掉下来,发现后面的"房子"却丢在了树上面, 现在这 只蜗牛要求寻找它的房子,它又得从树根开始爬起,现在要求一条路径使得其找到房子 所要爬行的期望距离最小. 爬行距离如下计算, 题目规定每一个分支和枝末都看做是 一个节点, 这些节点之间的距离都是1, 在分支上可能会有热心的毛毛虫, 这些毛毛虫 会如实的告诉蜗牛他之前是否经过这条路径, 也正是因为毛毛虫, 因此询问毛毛虫的顺 序使得这题的期望是不同的. 输入数据时给定的一个邻接关系,通过上一个节点来构图 同时字符 'Y'表示该点有毛毛虫, 字符'N'表示该点 解法:dp[i][0]表示以该点为根的节点找不到房子时要爬行最少的距离, 这个值有什么用呢? 这个值就是用去计算房子落在其他叶子节点时,其对爬行距离的负面效应有多大. dp[i][1]表示以该点为根的节点在选择好所有分支点的爬行方案后,枚举完房子落在该 子树所有叶子节点上的总爬行距离的最小值,这是一个值告诉我们这棵子树对爬行距离 的正面效应有多大.那么有动态方程: ch[x]表示x节点一共有多少个孩子节点 dp[i][0] = sum{ dp[j][0] + 2 } 当i没有毛毛虫且要求j是i的孩子节点,这个是很好 理解的, 多出来的2就是连接该孩子节点的边来回的两次 dp[i][0] = 0 当该点有毛毛虫的时候, 原因是因为毛毛虫会告诉我们这点下面没有房子 当一个节点时叶子节点的时候,那么 dp[i][0] = dp[i][1] = 0; 要明确dp[i][1]是表示在遇到分支选择的先后顺序决定后,我们枚举房子在其各个叶子 上的所要爬行的总距离 dp[i][1] = sum{ (sum{dp[1..j-1][0]+2}+1}*ch[j] + dp[j][1]}, 其中j是i的孩子 这个方程要怎么去理解呢? 意思翻译过来就是遍历i的孩子中的j号子树所有叶子节点所 要爬行的最短距离.其值就是: 前面[1, j-1]号子树没有找到节点所爬行的最短距离加上走了的多余的边再加上遍历j 号子树所有叶子节点所爬行的最短距离, 那么这里显然谁前谁后就会决定最后值的大小 现在只考虑序列中任意两棵子树A,B, 如果A放前面的话, 枚举完所有房子所在位置后的总距离就是 ans1 = (ch[A] + dp[A][1]) + ((dp[A][0]+2)*ch[B] + dp[B][1] + ch[B]) 前一个括号是假设枚举房子落在A的所有叶子上, 后面的扩后是枚举在B的所有叶子上 ans2 = (ch[B] + dp[B][1]) + ((dp[B][0]+2)*ch[A] + dp[A][1] + ch[A]) ans1 - ans2 = (dp[A][0]+2)*ch[B] - (dp[B][0]+2)*ch[A]*/
·
0 0
- The Lost House--经典树形DP
- POJ 2057 The Lost House 经典树形DP+贪心
- 【树形DP】【poj 2057】The Lost House
- poj_2057 The Lost House(树形dp)
- POJ 2057 The Lost House 树形DP+贪心
- pku 2057 The Lost House 树形dp+背包dp 解题报告
- POJ 2057 The Lost House 树状DP
- pku2057 The Lost House
- poj2057--The Lost House(树状dp,求期望)
- 【Poj 2507】The Lost House(树型dp)
- POJ 2057 The lost house
- poj 2057 The Lost House
- POJ 2057 The Lost House
- POJ 2057 The Lost House
- POJ 2057 The Lost House
- poj-2057 The Lost House
- 【POJ2057】The Lost House【TreeDP】
- poj 2057 The Lost House
- pipe小实例
- The Suspects poj 1611 幷查集
- android 字符串转流
- VS2013中ASP.NET使用MD5加密注意事项
- muicss
- The Lost House--经典树形DP
- [Leetcode] Remove Duplicates from Sorted Array
- Hadoop Streaming原理及实践
- laravel基础之文件上传
- 深度学习笔记一:生成对抗网络(Generative Adversarial Nets)
- cocoapods使用指南【转】
- Java开发WebService
- mui官网
- Android 简易指南针


