王小草【机器学习】笔记--EM算法

标签（空格分隔）： 王小草机器学习笔记

---

EM算法的英文全称是Expectation Maximization Algorithm，也就是求期望最大化，也就是我们常说的目标函数求最大值的算法。EM算法，直观的说，就是有一堆未知的数据（比如一些特征值），这些数据可能来自于不同的类别，而你想知道的是每一个数据都来自于哪个类别，并且知道来自于这个类别的概率是多少。而在EM算法看来，每一个类别中的数据必然服从了某个固有的分布（如二项分布，正态分布等），只要寻找它密度函数的参数，就能知道数据的分布，所以EM使用了极大似然估计的方法去估计了各个分布的参数，从而进行了无监督地聚类。

本文首先会回顾和复习一下EM算法中要涉及到的知识：Jensen不等式和最大似然估计；
然后介绍EM算法，并且会用混合高斯GMM来作为例子用EM算法求解。
最后，会给出一些实现EM算法的python实例。

1. 回顾

1.1 回顾Jensen不等式

Jensen不等式这个名字有点陌生，但是如果眼睁睁地看到这个不等式，你肯定会觉得特别特别熟悉，并且鼻尖传来阵阵数学考试卷的味道，它会出现在选择题填空题或者后面的大分推导题中。万万没想到，今天还会在那么重要的算法中遇到。

假设有两个变量x1,x2,有一个函数f(),并且函数f是凸函数，那么就肯定有以下不等式成立：

f(θx1 + (1-θ)x2) <= θf(x1) + (1-θ)f(x2)

在二维坐标中表示如下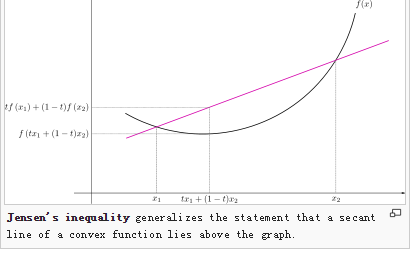

同理，若有多个x，多个θ，只要满足f是凸函数，并且
θ1，θ2，…θk >= 0;且θ1+θ2+…+θk = 1
那么下面不等式肯定成立：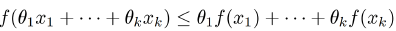

上面讲的是离散型的变量，针对连续型的变量，Jesen不等式也是成立的。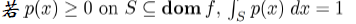

中θ是随机变量，分别与xi相乘后相加，其实就是在求x的期望值，那么以上任何形式的不等式，都可以表示成如下：

1.2 回顾K-means算法

之所以要在EM算法中回顾K-means，是因为在迭代k-means中其实就是不断取均值点求期望的过程，于EM迭代求最大化期望类似。

先初始选择k个簇中心，然后根据各个样本点到中心的距离来分割，再对分割后的类找到这个类中所有样本点的中心点（均值点）作为新的簇中心，然后再进行聚类，再找新的中心，如此循环，直到满足终止条件而停止。

这里，通过各个样本的均值来确定新的中心点其实就是在求期望，其过程的大致思路其实与我们接下去要讲的EM算法是类似的。

k-means能够非常方便得将样本分成若干簇，但是由一个巨大的问题是，我们无法知道这个样本点属于这个簇的概率，我们只知道属于或不属于的布尔值，如此一来，就没那么好玩了。

那么如果想知道概率的话，就得去找到与样本分布最接近的概率分布模型，要得到概率分布模型，就得先将模型中的参数估计出来。EM算法所实现的就是这个功能。

2.最大似然估计求参数

2.1 小引子

先来看一个简单的例子。
简单的例子一般都离不开抛硬币来。

假设我们现在不知道抛硬币出现正反面的概率，然后设每抛一次出现正面的概率是p，这个p是我们想求得的。
现在我做一个实验，将硬币抛是10次，然后记录结果为：正正反正正正反反正正。
最大似然估计就是去求出现以上这10次结果的概率最大时候，去估计p的概率。
因为每次抛硬币是一个独立事件，所以每一次抛硬币的概率是可以相乘的，于是以上10次结果发生的概率可以写成：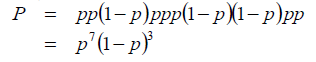

要求的P最大时p的值，其实就是对以上等式求目标函数最优化的过程，最后可以求出p=0.7。

当然，你肯定会义正言辞地说，不对！抛硬币的概率谁不知道呢，正反两面出现的概率都是0.5呀！
这是因为我们这个实验中只抛了10次，样本量太小存在的误差会偏大，如果抛100次，1000次，10000次，样本中正反两面出现的次数会越来越趋于1:1，那么求出来的p值肯定也会更接近与0.5了。

当然，你肯定还会义正言辞得说，可是这个极大似然估计有什么用吗，抛硬币的概率我本来就知道。嗯，对，抛硬币只是一个例子。假如我收集了上海9月份30天的天气数据，想知道9月份的上海下雨的概率p有多大；再假如我记录了今年我从东昌路上2号线有没有座位的数据，想知道上车后有座位的概率p是多少；再假如我有所有进入购物网站的行为数据样本，想知道首次进来的人会购买下单的概率；再假如二号店若推出新品促销的广告，用户看到会点击进入的概率…等等。这些概率我想你应该不知道，但作为商家也许会非常渴望知道。

2.2 二项分布的最大似然估计

抛硬币其实是一个二项分布，它有两个值，概率分别为p和1-p。
假设投掷N次硬币，出现正面朝上次数是n，反面朝上的次数是N-n。
并且设正面朝上的概率是p。
现在使用似然函数来求目标函数的最优化，为了计算方便，我们将函数取对数来求最大值，成为“对数似然函数”。
目标函数如下：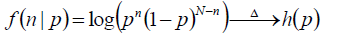

对目标函数中的p求导数，最后得到p = n/N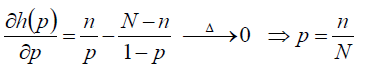

以上就是用最大似然函数估计二项分布参数的过程。

2.3 高斯分布的最大似然估计

现在我们来看一看高斯分布。
若给定一组样本X1,X2,X3…Xn，已知他们是来自于高斯分布N（μ，σ)，即符合均值为μ，标准差为σ的正太分布。要根据这些样本点的分布去估计这个正态分布的参数μ，σ。

1.首先，要知道高斯分布的概率密度函数：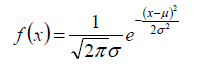

里面有两个参数，分别就是μ，σ。也是我们要求的参数。

2.要得到样本点那样分布的概率，假设每个样本都是独立的，所有总的概率就是每个样本的概率的乘积：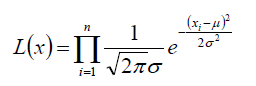

3.对上面的等式进行对数似然函数的化简：

4.得到化简后的目标函数：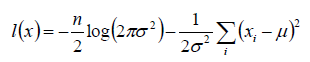

现在就是对这个目标函数求最大值时的参数μ，σ的值

5.将目标函数分别对参数μ，σ进行求导，就能求出μ，σ的公式：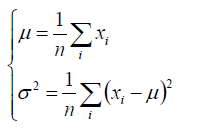

以上就是用最大似然函数估计高斯分布参数的过程。

3.EM算法

经过了冗长的铺垫终于到了本文的重点了–EM算法。在讲EM算法乏味难懂的定理前，我们先用高斯混合模型来走一遍它的参数估计

3.1 直观理解猜测GMM的参数估计

已知一个学校的所有学生的身高样本（X1,X2,X3…Xn），并且男生和女生都分别服从N（μ男，σ男）和N（μ女，σ女）的高斯分布。目的是要求出μ男，σ男，μ女，σ女这四个参数。

来来来理一下这个题目，与上文中的例子不同了，现在同时有两个高斯分布混合在一起，我们要去求出两个高斯分布各自的均值与标准差参数。那么问题来了…我怎么知道某个样本属于男高斯还是女高斯啊，现在我们只知道所有的身高值，并不知道这些身高背后的性别呀。恩恩，这是一个混合高斯模型，简称GMM（随机变量是由2个高斯分布混合而成）。在GMM中，有一个隐藏的随机变量我们没法看到，那就是性别，因为无法知道性别的概率，也就无法知道某个样本属于哪个高斯分布的了。所以这个隐藏的概率π男，π女也是我们需要估计的，它表示某个样本属于某个高斯分布的概率。

将上面的例子扩展地表示出来：随机变量X是由K个高斯分布混合而成，取各个高斯分布的概率为π1，π2，π3…πk；第i个高斯分布的均值为μi,方差为Σi。若观测到随机变量X的一系列样本X1,X2,X3…Xn，试估计参数π，μ，Σ。

1.建立目标函数
同样的，我们使用对数似然函数来建立目标函数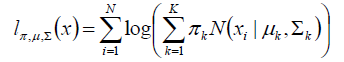

由于对数函数里面又有加和，无法直接用求导解方程的方法来求最大值。为了解决这个问题，接下来分两步走。

2.第一步：估计数据来自哪个组（也就是说来自哪个高斯分布）
首先我们根据经验随便给定π，μ，Σ的先验值。
然后求r(i,k),表示，样本i 由高斯分布k生成的概率。公式如下：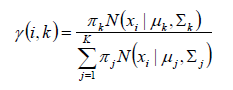

根据这个公式，我们可以求得样本X1分别属于K1,K2,K3..的概率

3.第二步：估计每个高斯分布中的参数
对于高斯分布k来说，它说生成的点可看成是{r(i,k)*xi|i-=,1,2,3..N}，就是所有原来的样本点乘以它属于高斯分布k的概率，从而得到了新的样本点，这些样本点应是服从高斯分布k的。因此高斯分布k的样本个数不再是原来的N，而是所有样本属于它的概率的加和：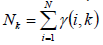
同理，π，μ，Σ都可以因此重新计算：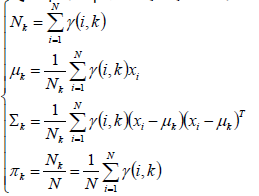

4.重复第一步，第二步
我们用先验的π，μ，Σ计算出来新的π，μ，Σ，于是又可以利用新的π，μ，Σ去计算新的r(i,k)，再得出又一轮新的π，μ，Σ，如此循环往复，这些参数会慢慢收敛，直到前后两次的差值小于预先设定的阀值，就停止迭代，最后一次算出的π，μ，Σ就可以当成最终的估计值啦。

3.2 EM算法的提出

问题的提出：
假设有训练样本X1,X2,X3…Xm，包含m个独立样本，希望从中找出p(x,z)的参数。

通过似然估计建立目标函数：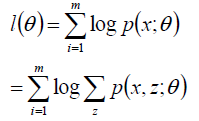

x是样本点，z是隐藏参数（就是上文中的π），θ是显参数（就是上文高斯分布中的μ，σ）

z是隐藏随机变量，不方便直接找到参数估计。所以使用策略：计算l(θ)的下界，求出该下界的最大值，重复该过程知道收敛，下图中绿线所经过的点是下界与l(θ)相等的点，求下界的最大值，往往会更接近目标函数的最大值。

设Qi是z的某一个分布，那么目标函数可以转换：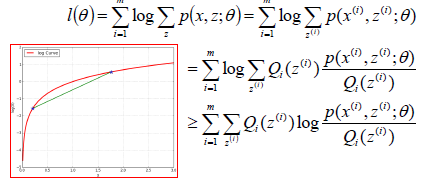

log函数是一个凹函数，要求的一个点与它相等，只能使得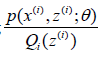是一个常数，也就是：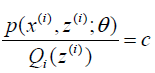

进一步分析：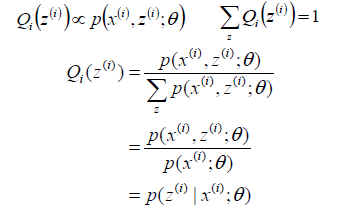

到后来，居然发现Q(z)其实就是z关于样本xi，参数θ的条件概率

由此，可以归纳出EM算法的整体框架：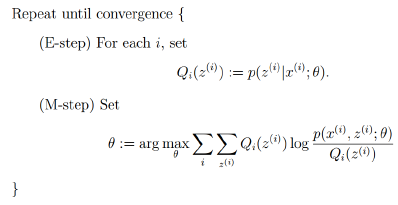

3.3 理论公式推导GMM

还是3.1中的例子：
已知一个学校的所有学生的身高样本（X1,X2,X3…Xn），并且男生和女生都分别服从N（μ男，σ男）和N（μ女，σ女）的高斯分布。目的是要求出μ男，σ男，μ女，σ女这四个参数。

E-STEP: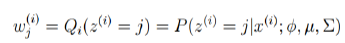

M-STEP:
将多项式和高斯分布等参数带入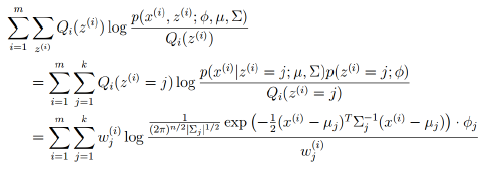

对均值求偏导，求均值：

上式等于0解均值为：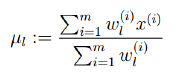

对方差求偏导，求方差：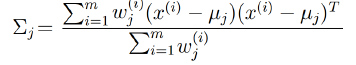

对多项式中的参数：
考察m-step中的目标函数，对于φ，删除常数项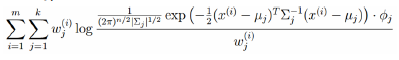

得到：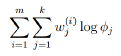

由于多项式的概率和为1，建立拉格朗日方程：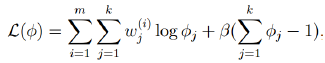

求偏导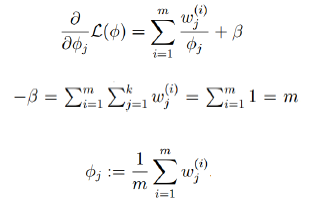

于是我们仍然可以得到参数的估计方程：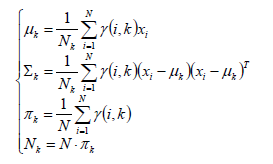

与3.1相比，得到了相同的结果！

---

5. Python实现

5.1 EM算法估算GMM均值

这个例子是我网上找的，注释不多，所以我将每句代码都写了注释以方便理解。

第一个方法ini_data是生成了一组由两个高斯分布产生的样本数据，他们的方差相同，均值不同。
第二个方法e_step是EM算法的第1步，先初始化参数，然后根据已知的参数去估计概率π
第三个方法M-step是EM算法的第2步，根据e-step中计算出来的π去估计新的μ和σ
第四个方法run是去不断迭代循环e-step和m-step直至收敛求得最终的三个参数的估计值

#!/usr/bin/python# -*- coding:utf-8 -*-import mathimport copyimport numpy as npimport matplotlib.pyplot as pltis_debug = False# # 创建两个正态分布的数据，方差已知并同，均值不同，k是高斯分布的个数，n是样本数def ini_data(sigma, mu1, mu2, k, n):    global x    global mu    global expectations    # 创建1*n维的0向量    x = np.zeros((1, n))    # 随机生成两个0-1间的随机数    mu = np.random.random(2)    # 生成n*k维的0向量    expectations = np.zeros((n, k))    # 遍历    for i in xrange(0, n):        # 如果生成一个随机数大于0.5        if np.random.random(1) > 0.5:            # 那么x中第0行第i列由第1个高斯分布生成            x[0,i] = np.random.normal()*sigma + mu1        # 如果小于0.5        else:            # 则由第2个高斯分布生成随机数            x[0,i] = np.random.normal()*sigma + mu2    if is_debug:        print "***"        print u"初始观测值数据x:"        print x# # 计算E[Zij]隐藏参数def e_step(sigma, k, n):    global expectations    global mu    global x    # 对每个样本做遍历    for i in xrange(0, n):        # 初始化新的样本数        denom = 0        # 对该样本在每个分布中做遍历        for j in xrange(0, k):            # 累加计算所有样本点在该分布中的数            denom += math.exp((-1/(2 * float(sigma ** 2))))*(float(x[0,i] - mu[j]) ** 2)        for j in xrange(0, k):            # 计算该样本点在该分布中的数            numer = math.exp((-1/(2 * float(sigma ** 2))))*(float(x[0,i] - mu[j]) ** 2)            # 计算该样本点来自该分布的概率r(i,k)            expectations[i,j] = numer / denom    if is_debug:        print "***"        print u"隐藏变量E(Z)"        print expectations# # M-step:求最大化E(Zij)时的参数mudef m_step(k, N):    global expectations    global x    # 遍历每个分布    for j in xrange(0, k):        # 初始化新的样本点的值        numer = 0        # 初始化新的样本数量        denom = 0        # 对每个新样本做遍历        for i in xrange(0, N):            # 累加所有样本的值            numer += expectations[i, j] * x[0, i]            # 累加所有样本的数量            denom += expectations[i, j]        # 计算新的均值        mu[j] = numer / denom# # 迭代收敛def run(sigma, mu1, mu2, k, n, iter_num, epsilon):    # 生成由两个正态分布组成的数据    ini_data(sigma, mu1, mu2, k, n)    print u"初始化均值：", mu    # 根据预先设置的迭代次数循环    for i in range(iter_num):        # 将现有的均值赋值给老的均值变量        old_mu = copy.deepcopy(mu)        # 计算隐变量的期望        e_step(sigma, k, n)        # 求目标函数最大值时的均值        m_step(k, n)        print i, mu        # 如果新旧均值的差值小于设定的阀值则终止循环        if sum(abs(mu - old_mu)) < epsilon:            breakif __name__ == '__main__':    run(6, 40, 20, 2, 10000, 10, 0.01)    plt.hist(x[0, :], 50)    plt.show()

最后一个方法将这组数据在二维坐标上画出来了，图像如下，确实可以很清晰地看出有两个正态分布，他们的均值不同，但方差类似。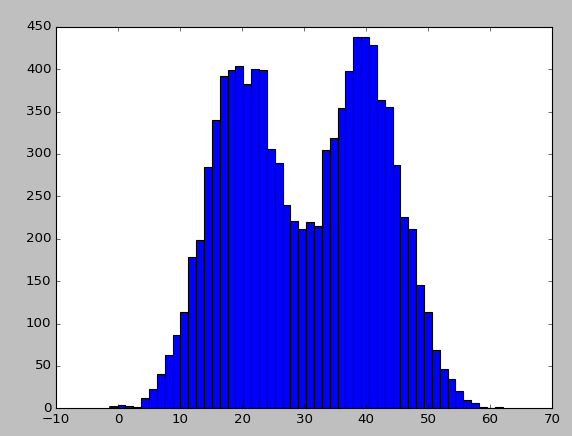

打印出迭代了10次的均值结果：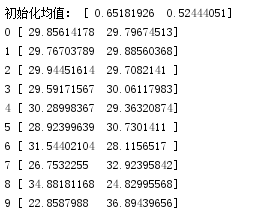

初始化的均值是随机的，非常小，与我们实际的均值差别非常大，在经过第一次迭代后，就已经有了明显的改善了，接下来每次迭代的结果都越来越接近真实的均值40,20了，可以看到如果迭代次数增加到100，或1000,EM估计出来的结果应该会非常接近40和20的。

# !/usr/bin/python# -*- coding:utf-8 -*-import numpy as npfrom scipy.stats import multivariate_normalimport matplotlib as mplimport matplotlib.pyplot as pltmpl.rcParams['font.sans-serif'] = [u'SimHei']mpl.rcParams['axes.unicode_minus'] = False# # 生成来自两个高斯分布的数据if __name__ == '__main__':    # 第一个分布的均值    mu1 = (0, 0, 0)    # 创建一个维度为3的单位矩阵，作为方差    cov1 = np.identity(3)    # 根据均值与方差随机生成多元的正太分布的数据    data1 = np.random.multivariate_normal(mu1, cov1, 100)    # 第二个分布的均值    mu2 = (2, 2, 1)    # 设置方差    cov2 = np.identity(3)    # 根据均值与方差随机生成第二个多元的正太分布的数据    data2= np.random.multivariate_normal(mu2, cov2, 100)    # 将两组数据union    data = np.vstack((data1, data2))    # 设置迭代次数    num_iter = 100    # 样本数据的大小，n是样本数的个数，d是维度，这里是3维    n, d = data.shape    # 初始化参数，随机设定即可    mu1 = np.random.standard_normal(d)  # 从三维的标准正态分布中随机取一个点作为初始均值    mu2 = np.random.standard_normal(d)    sigma1 = np.identity(d)  # 建立d维的单位矩阵作为初始化的方差    sigma2 = np.identity(d)    pi = 0.5 # 再拍脑门决定一下隐参数的值    # # 进行EM算法    for i in range(num_iter):        # E-step        # 根据均值方差创建两个正太分布        norm1 = multivariate_normal(mu1, cov1)        norm2 = multivariate_normal(mu2, cov2)        # 分布计算每个样本点由两个分布产生的概率        tau1 = pi*norm1.pdf(data)        tau2 = (1 - pi)*norm2.pdf(data)        # 计算由第一个分布产生的概率        gamma = tau1/(tau1 + tau2)        # M-step        mu1 = np.dot(gamma, data)/sum(gamma)        mu2 = np.dot((1-gamma), data)/sum(1-gamma)        sigma1 = np.dot(gamma * (data - mu1).T, (data - mu1))/sum(gamma)        sigma2 = np.dot((1-gamma) * (data - mu2).T, (data - mu2))/sum(1-gamma)        pi = sum(gamma)/n        # if i % 2 == 0:        #     print i, ":\t",mu1, mu2    print '类别概率：\t', pi    print '均值：\t', mu1, mu2    print '方差：\t', sigma1, sigma2    g = GMM(n_components=2, covariance_type="full", n_iter=100)    g.fit(data)    print '类别概率:\t', g.weights_[0]    print '均值:\n', g.means_, '\n'    print '方差:\n', g.covars_, '\n'    # 预测分类    norm1 = multivariate_normal(mu1, sigma1)    norm2 = multivariate_normal(mu2, sigma2)    tau1 = norm1.pdf(data)    tau2 = norm2.pdf(data)    # figsize设置画布的大小,facecolor设置画布背景色为白色    fig = plt.figure(figsize=(14, 7), facecolor='w')    # 121表示画1行2列中的第1个图：原始数据的分布图    ax = fig.add_subplot(121, projection='3d')    # x,y,z坐标是原始数据的第1,2,3列数据，c是颜色为蓝色，s是三点的大小，marker是三点的形状为圆，depthshade为颜色需不需要分深浅度    ax.scatter(data[:, 0], data[:, 1], data[:, 2], c='b', s=30, marker='o', depthshade=True)    # 设置坐标的标记    ax.set_xlabel('X')    ax.set_ylabel('Y')    ax.set_zlabel('Z')    # 设置图像的名称与此题大小    ax.set_title(u'origin data', fontsize=18)    # 画1行2列中的第2个图：预测数据的分类图    ax = fig.add_subplot(122, projection='3d')    # 提取出概率在分布1中比分布2中大的样本点    c1 = tau1 > tau2    # 将这点画在第2张图中，颜色为红色，形状是小圆    ax.scatter(data[c1, 0], data[c1, 1], data[c1, 2], c='r', s=30, marker='o', depthshade=True)    # 同理，拿出在分布2中概率大的样本点    c2 = tau1 < tau2    # 用绿色的小三角表示    ax.scatter(data[c2, 0], data[c2, 1], data[c2, 2], c='g', s=30, marker='^', depthshade=True)    ax.set_xlabel('X')    ax.set_ylabel('Y')    ax.set_zlabel('Z')    ax.set_title(u'EM算法分类', fontsize=18)    # 自动调整图像大小，使两个图形比较紧凑    plt.tight_layout()    # 画出来吧，少年    plt.show()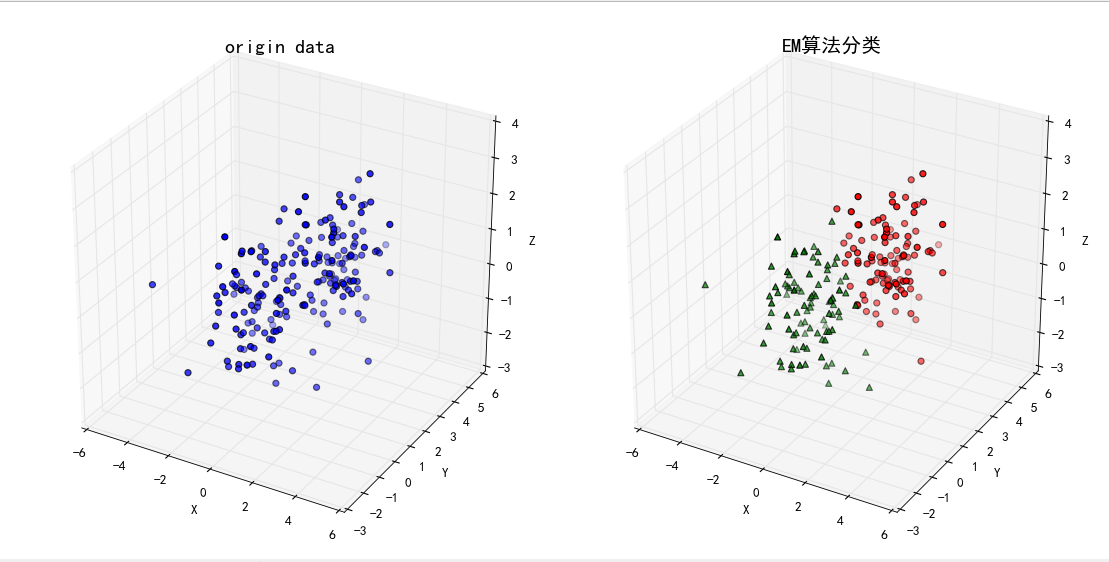

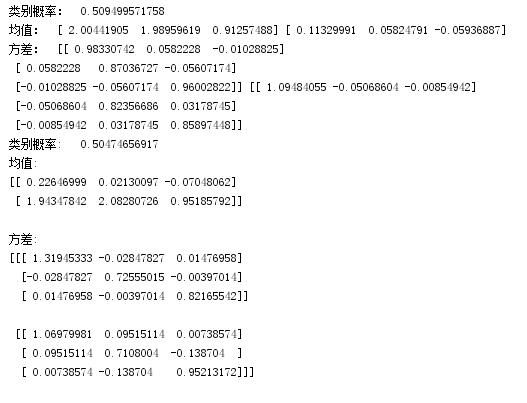
# !/usr/bin/python# -*- coding:utf-8 -*-import numpy as npfrom scipy.stats import multivariate_normalfrom sklearn.cross_validation import train_test_splitfrom sklearn.mixture import GMMimport matplotlib as mplimport matplotlib.pyplot as pltimport matplotlib.colorsmpl.rcParams['font.sans-serif'] = [u'SimHei']mpl.rcParams['axes.unicode_minus'] = Falsedef expand(a, b):    d = (b - a) * 0.05    return a-d, b+dif __name__ == '__main__':    # 读入数据（性别，身高，体重）    data = np.loadtxt('D:\Documents\cc\python\data\HeightWeight.csv',                      dtype = np.float, delimiter=',', skiprows=1)    # 将数据分成两部分y:性别标签列，x:身高与体重2列,[1, ]表示第一部分取[0,1)列，第二部分取剩下的列    y, x = np.split(data, [1, ], axis=1)    # 将数据分成训练集与测试集，random_state保证了随机池相同    x, x_test, y, y_test = train_test_split(x, y, train_size=0.6, random_state=0)    # 用生成一个GMM，由两个分布组成，tol是阀值    gmm = GMM(n_components=2, covariance_type='full', tol=0.0001, n_iter=100, random_state=0)    # 分别取出身高与体重的最大值与最小值    x_min = np.min(x, axis=0)    x_max = np.max(x, axis=0)    # 使身高与体重的训练数据去拟合刚刚创建的gmm    gmm.fit(x)    # 打印均值，方差看一看    print '均值 = \n', gmm.means_    print '方差 = \n', gmm.covars_    # 对训练数据与测试数据都带入gmm做预测    y_hat = gmm.predict(x)    y_test_hat = gmm.predict(x_test)    # 以为gmm做预测是不会分两个分布的先后顺序的，所以要保证是顺序颠倒的时候女性仍然表示为0    change = (gmm.means_[0][0] > gmm.means_[1][0])    if change:        z = y_hat == 0        y_hat[z] = 1        y_hat[~z] = 0        z = y_test_hat == 0        y_test_hat[z] = 0        y_test_hat[~z] = 0    # 求训练与测试集的准确率    acc = np.mean(y_hat.ravel() == y.ravel())    acc_test = np.mean(y_test_hat.ravel() == y_test.ravel())    acc_str = u'训练集准确率：%.2f%%' % (acc * 100)    acc_test_str = u'测试集准确率：%.2f%%' % (acc_test * 100)    print acc_str    print acc_test_str    # 创建浅色的颜色（用来做背景）和深色的颜色（用来表示点）    cm_light = mpl.colors.ListedColormap(['#FF8080', '#77E0A0'])    cm_dark = mpl.colors.ListedColormap(['r', 'g'])    # 分别取两个特征的最大值与最小值    x1_min, x1_max = x[:, 0].min(), x[:, 0].max()    x2_min, x2_max = x[:, 1].min(), x[:, 1].max()    x1_min, x1_max = expand(x1_min, x1_max)    x2_min, x2_max = expand(x2_min, x2_max)    # 在画布上画上横纵坐标网格各500    x1, x2 = np.mgrid[x1_min:x1_max:500j, x2_min:x2_max:500j]    # 将两个特征的数铺平成一列    grid_test = np.stack((x1.flat, x2.flat), axis=1)    # 用gmm做预测y值    grid_hat = gmm.predict(grid_test)    # 将预测出来的y值调整大小成与x1一致    grid_hat = grid_hat.reshape(x1.shape)    if change:        z = grid_hat == 0        grid_hat[z] = 1        grid_hat[~z] = 0    # 画一个9*7的画布，背景色为白色    plt.figure(figsize=(9, 7), facecolor='w')    # 用之前设置的浅颜色来做两个分布的区分区域    plt.pcolormesh(x1, x2, grid_hat,cmap=cm_light)    # 画训练样本点，用圆表示，并使用之前设置的深色表示    plt.scatter(x[:, 0], x[:, 1], s=50, c=y, marker='o', cmap=cm_dark, edgecolors='k')    # 画训练样本点，用三角形表示，并使用之前设置的深色表示    plt.scatter(x_test[:, 0], x_test[:, 1], s=60, c=y_test, marker='^', cmap=cm_dark, edgecolors='k')    # 奔跑吧，少年    plt.show()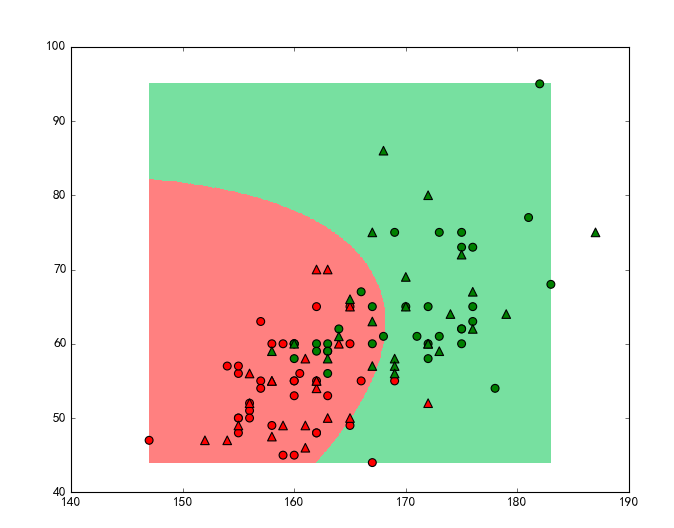

# !/usr/bin/python# -*- coding:utf-8 -*-import numpy as npfrom sklearn.mixture import GMM, DPGMMfrom sklearn.cross_validation import train_test_splitimport matplotlib as mplimport matplotlib.colorsimport matplotlib.pyplot as pltmpl.rcParams['font.sans-serif'] = [u'SimHei']mpl.rcParams['axes.unicode_minus'] = Falsedef expand(a, b, rate = 0.05):    d = (b - a) * rate    return a-d, b+ddef accuracy_rate(y1, y2):    acc1 = np.mean(y1 == y2)    acc = acc1 if acc1 > 0.5 else 1-acc1    return accif __name__ == '__main__':    # 设置随机池    np.random.seed(0)    # 设置协方差    cov1 = np.diag((1, 2))    # 设置生成随机数的个数    N1 = 500    N2 = 300    N = N1 + N2    # 生成正态分布的随机数    x1 = np.random.multivariate_normal(mean=(3, 2), cov=cov1, size=N1)    # 创建一个数组    m = np.array(((1, 1), (1, 3)))    # 将x1与新数组做点乘，目的是做一个转换    x1 = x1.dot(m)    x2 = np.random.multivariate_normal(mean=(-1, 10), cov=cov1, size=N2)    # union两组随机数    x = np.vstack((x1, x2))    # 设定它们的y值    y = np.array([0]*N1 + [1]*N2)    # 类型    types = ('spherical', 'diag', 'tied', 'full')    err = np.empty(4)    bic = np.empty(4)    # 对类型进行枚举，i是索引    for i, type in enumerate(types):        gmm = GMM(n_components=2, covariance_type=type, random_state=0)        gmm.fit(x)        err[i] = 1 - accuracy_rate(gmm.predict(x), y)        bic[i] = gmm.bic(x)    print '错误率：', err.ravel()    print 'BIC：', bic.ravel()

错误率： [ 0.44625  0.3625   0.30625  0.     ]BIC： [ 8291.31989604  8189.04587246  8290.20374814  6850.90774844]均值 = [[ -0.98545235  10.07568825] [  4.88245339   8.69755024]]方差 = [[[  0.89173153  -0.02570634]  [ -0.02570634   1.95207306]] [[  2.86753624   6.6289323 ]  [  6.6289323   17.97477745]]]