开尔文船波

来源：互联网发布：游族网络被告编辑：程序博客网时间：2024/06/16 22:00

[编辑]

维基百科，自由的百科全书

开尔文船波

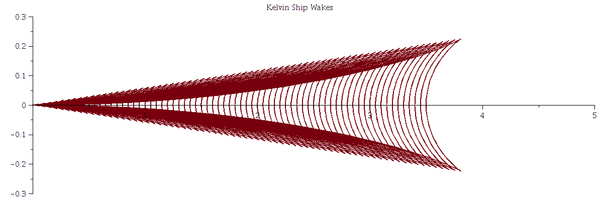
开尔文船波（Kelvin Wake, Kelvin ship wave）。鸭子或船只在深水湖面经过时，在后面会激起一道V形的波。开尔文男爵最先对船波进行数学研究，因此称为开尔文船波。船波动形状和福禄数{\displaystyle Fr} $Fr$ 有密切关系。

{\displaystyle Fr={\frac {V}{\sqrt {gl}}}} $Fr={\frac {V}{\sqrt {gl}}}$

其中g为重力常数，V是船速，l是船的长度。

令船的长度{\displaystyle l=k*{\frac {V^{2}}{g}}} $l=k*{\frac {V^{2}}{g}}$ 则{\displaystyle Fr={\frac {1}{\sqrt {k}}}} $Fr={\frac {1}{\sqrt {k}}}$ .

对于长度大而速度低的轮船，Fr数小，开尔文船波主要是长波，其波前与速度矢量的夹角比较小。

而小快艇，长度小，速度高，Fr 数大，开尔文船波则以短波长的水波为主，而波前则与速度数量成较大的夹角。^[1]

开尔文船波动研究，对于船舶的设计有重要意义，因为船舶的马力，有一部分消耗在激起船波。利用Fr数与速度成正比，与长度的平方根成反比的规律，可以利用小的模型，缩小船长{\displaystyle M^{2}} $M^{2}$ 倍，同时缩小速度M倍，可以在实验室中模拟海上巨舟。^[2]

多鞍点函数积分[编辑]

Integrand of Kelvin Wake Integral

Kelvin Ship Wake Integrand contour Maple plot

当船只以速度V驶过深水湖面，波形的幅度在相对于船只为静止的极坐标（{\displaystyle \rho ,\phi } $\rho ,\phi$ 中在船只的速度矢量方向，{\displaystyle \phi =0} $\phi=0$ ），由下列公式表示^[3]

{\displaystyle K(\phi ,\rho )=\int _{-\pi /2}^{\pi /2}cos(\rho {\frac {cos(\theta +\phi )}{cos^{2}\theta }}d\theta } $K(\phi ,\rho )=\int _{-\pi /2}^{\pi /2}cos(\rho {\frac {cos(\theta +\phi )}{cos^{2}\theta }}d\theta$

其中{\displaystyle \rho =gr/V^{2}} $\rho =gr/V^{2}$

{\displaystyle {\frac {1}{\rho }}={\frac {V^{2}}{gr}}} ${\frac {1}{\rho }}={\frac {V^{2}}{gr}}$ 是福禄数的平方{\displaystyle Fr^{2}} $Fr^{2}$

{\displaystyle g} $g$ 为重力常数{\displaystyle l} $l$ 为船的长度。

上列K函数是下列多鞍点积分的正数部分：

{\displaystyle K(\phi ,\rho )=Re(\int _{-\infty }^{\infty }\exp(i*\rho *f(\theta ,\rho )d\theta )} $K(\phi ,\rho )=Re(\int _{-\infty }^{\infty }\exp(i*\rho *f(\theta ,\rho )d\theta )$ 其中，多鞍点积分的核函数为

{\displaystyle f(\theta ,\phi )=-{\frac {cos(\theta +\phi )}{cos^{2}\theta }}} $f(\theta ,\phi )=-{\frac {cos(\theta +\phi )}{cos^{2}\theta }}$

此核函数是一个多鞍点函数，振荡剧烈如图

求其极点，

{\displaystyle {\frac {df(\theta ,\phi )}{d\theta }}={\frac {sin(\theta +\phi )}{cos(\theta )^{2}}}-{\frac {2*cos(\theta +\phi )*sin(\theta )}{cos(\theta )^{3}}}=0} ${\frac {df(\theta ,\phi )}{d\theta }}={\frac {sin(\theta +\phi )}{cos(\theta )^{2}}}-{\frac {2*cos(\theta +\phi )*sin(\theta )}{cos(\theta )^{3}}}=0$

解之，得

{\displaystyle \theta _{1}=arctan({\frac {(1/4)*(1+{\sqrt {(1-8*tan(\phi )^{2}))}}}{tan(\phi )}})=-arctan({\frac {(1/4)*(-1+{\sqrt {(}}1-8*tan(\phi )^{2}))}{tan(\phi )}})} $\theta _{1}=arctan({\frac {(1/4)*(1+{\sqrt {(1-8*tan(\phi )^{2}))}}}{tan(\phi )}})=-arctan({\frac {(1/4)*(-1+{\sqrt {(}}1-8*tan(\phi )^{2}))}{tan(\phi )}})$

由此

{\displaystyle \phi _{1}=19.47} $\phi _{1}=19.47$ 度,

{\displaystyle \phi _{2}=-19.47} $\phi _{2}=-19.47$ 度

这就是凯尔文船波的V型波包线的夹角，最早由凯尔文男爵发现，而且角度与船速无关.^[4]^[5]至于波纹本身则与船速矢量的夹角为

{\displaystyle \theta =\pi -19.47=35.3} $\theta =\pi -19.47=35.3$ °^[1]

开尔文驻相法[编辑]

Kelvin Wake (Maple density plot)

开尔文船波波形

开尔文船波积分{\displaystyle K(\phi ,\rho )} $K(\phi ,\rho )$ 必须通过数值积分计算。开尔文男爵根据被积分函数在积分区间内剧烈震荡的特点，提出了驻相法（Method of Stationary Phase）。

原理：当被积分函数剧烈震荡时，除了在极点外，震荡的被积分函数正负相抵消，因此可以将此被积分函数在极点的值作为整个积分的近似，驻相法乃是拉普拉斯方法的推广。^[6]

被积分函数 {\displaystyle f(\theta ,\phi )=-{\frac {cos(\theta +\phi )}{cos^{2}\theta }}} $f(\theta ,\phi )=-{\frac {cos(\theta +\phi )}{cos^{2}\theta }}$ 的两个极点是：

{\displaystyle \theta _{p}=arctan({\frac {(1/4)*(1+{\sqrt {(1-8*tan(\phi )^{2}))}}}{tan(\phi )}})} $\theta _{p}=arctan({\frac {(1/4)*(1+{\sqrt {(1-8*tan(\phi )^{2}))}}}{tan(\phi )}})$

{\displaystyle \theta _{m}=-arctan({\frac {(1/4)*(-1+{\sqrt {(}}1-8*tan(\phi )^{2}))}{tan(\phi )}})} $\theta _{m}=-arctan({\frac {(1/4)*(-1+{\sqrt {(}}1-8*tan(\phi )^{2}))}{tan(\phi )}})$

令

{\displaystyle f_{m}=f(\theta _{m},\phi )={\frac {sin((1/2)*\phi -(1/2)*arcsin(3*sin(\phi )))}{sin((1/2)*\phi +(1/2)*arcsin(3*sin(\phi )))}}} $f_{m}=f(\theta _{m},\phi )={\frac {sin((1/2)*\phi -(1/2)*arcsin(3*sin(\phi )))}{sin((1/2)*\phi +(1/2)*arcsin(3*sin(\phi )))}}$

{\displaystyle f_{p}=f(\theta _{p},\phi )={\frac {cos((1/2)*\phi +(1/2)*arcsin(3*sin(\phi )))}{cos(-(1/2)*\phi +(1/2)*arcsin(3*sin(\phi )))}}} $f_{p}=f(\theta _{p},\phi )={\frac {cos((1/2)*\phi +(1/2)*arcsin(3*sin(\phi )))}{cos(-(1/2)*\phi +(1/2)*arcsin(3*sin(\phi )))}}$

{\displaystyle fbar:=1/2*(f_{p}+f_{m})} $fbar:=1/2*(f_{p}+f_{m})$

{\displaystyle D2F={\frac {d^{2}F(\theta ,\phi )}{d\theta ^{2}}}} $D2F={\frac {d^{2}F(\theta ,\phi )}{d\theta ^{2}}}$

{\displaystyle D2F_{p}=D2F(\theta _{p},\phi )} $D2F_{p}=D2F(\theta _{p},\phi )$

{\displaystyle D2F_{m}=D2F(\theta _{m},\phi )} $D2F_{m}=D2F(\theta _{m},\phi )$

{\displaystyle \Delta :=(3/4*(f_{m}-f_{p}))^{(}2/3)} $\Delta :=(3/4*(f_{m}-f_{p}))^{(}2/3)$

{\displaystyle u={\sqrt {\frac {\Delta ^{1/2}}{2}}}*({\frac {1}{\sqrt {D2F_{p}}}}+{\frac {1}{\sqrt {-D2F_{m}}}})} $u={\sqrt {\frac {\Delta ^{1/2}}{2}}}*({\frac {1}{\sqrt {D2F_{p}}}}+{\frac {1}{\sqrt {-D2F_{m}}}})$

{\displaystyle v={\sqrt {\frac {2}{\Delta ^{1/2}}}}*({\frac {1}{\sqrt {D2F_{p}}}}-{\frac {1}{\sqrt {-D2F_{m}}}})} $v={\sqrt {\frac {2}{\Delta ^{1/2}}}}*({\frac {1}{\sqrt {D2F_{p}}}}-{\frac {1}{\sqrt {-D2F_{m}}}})$

{\displaystyle K(\phi ,\rho )\approx 2*\pi *(u*cos(\rho *fbar)*AiryAi(-\rho ^{(}2/3)*\Delta )/\rho ^{(}1/3)+v*sin(\rho *fbar)*AiryAi(1,-\rho ^{(}2/3)*\Delta )/\rho ^{(}2/3))} $K(\phi ,\rho )\approx 2*\pi *(u*cos(\rho *fbar)*AiryAi(-\rho ^{(}2/3)*\Delta )/\rho ^{(}1/3)+v*sin(\rho *fbar)*AiryAi(1,-\rho ^{(}2/3)*\Delta )/\rho ^{(}2/3))$

开尔文船波的波峰，由下列两个参数方程式描述^[7]

{\displaystyle x:=X*sin(\beta )*(1-(1/2)*sin(\beta )^{2})} $x:=X*sin(\beta )*(1-(1/2)*sin(\beta )^{2})$

{\displaystyle y:=X*sin(\beta )^{2}*cos(\beta )/(2*M)} $y:=X*sin(\beta )^{2}*cos(\beta )/(2*M)$

外部链接[编辑]

§36.13 Kelvin’s Ship-Wave Pattern

脚注[编辑]

^ ^1.0 ^1.1 James LightHill, p274
^ James Lighthill p275
^ Frank Oliver, p790-791
^ Shu, Jian-Jun. Transient Marangoni waves due to impulsive motion of a submerged body. International Applied Mechanics. 2004, 40 (6): 709–714. doi:10.1023/B:INAM.0000041400.70961.1b.
^ Shu, Jian-Jun. Transient free-surface waves due to impulsive motion of a submerged source. Underwater Technology. 2006, 26 (4): 133–137. doi:10.3723/175605406782725023.
^ Frank Oliver, p790-795
^ James LightHill,p277

参考文献[编辑]

Frank J. Oliver, NIST Handbook of Mathematical Functions, 2010, Cambridge University Press
Jame Lighthill Waves in Fluids, Cambridge University Press 1979

分类：

特殊函数
流体力学

1 0

开尔文船波

[编辑]

目录

多鞍点函数积分[编辑]

开尔文驻相法[编辑]

外部链接[编辑]

脚注[编辑]

参考文献[编辑]