线性收敛的随机优化算法之 SAG、SVRG（随机梯度下降）

来源：互联网发布：淘宝管理团队编辑：程序博客网时间：2024/06/04 19:00

原文出处：https://zhuanlan.zhihu.com/p/22402784?utm_source=tuicool&utm_medium=referral

这篇文章回顾了基于梯度的随机优化算法在这几年的重要发展 -- SAG、SVRG。

很多常见的机器学习模型的目标（比如最小二乘做线性回归、逻辑回归）都可以概括成以下这种一般形式：

$\min_{\mathbf{w}} \frac{1}{N} \sum_{i=1}^N f(\mathbf{x}_i, \mathbf{w}) + \lambda h(\mathbf{w})$

其中 $f(\mathbf{x}_i, \mathbf{w})$ 代表样本 $\mathbf{x}_i$ 的损失函数， $\mathbf{w}$ 是模型的参数， $h(\mathbf{w})$ 代表正则化项（用于控制模型复杂度或者模型稀疏度等等），有些时候这个正则化项是不平滑的，也就是说它可能不可导。

暂时先不考虑这个正则化项，只考虑样本上的损失，并且对符号做一点简化（ $f(\mathbf{x}_i,\mathbf{w}) \triangleq f_i(\mathbf{w})$ ），考虑下面这个优化目标：

$\min_{\mathbf{w}}\frac{1}{N}\sum_{i=1}^N f_i( \mathbf{w})$

这个形式非常简单，只要每个 $f_i(\mathbf{w})$ 都可导，就可以用梯度下降法（Gradient Descent）迭代求解:

$\mathbf{w}_{t+1} = \mathbf{w}_t - \eta \frac{1}{N}\sum_{i=1}^N \triangledown f_i(\mathbf{w}_t)$ ，其中 $\mathbf{w}_{t+1}$ 表示第 t+1 次更新后的参数。

梯度下降对于样本数目比较多的时候有一个很大的劣势，那就是每次需要求解所有样本的梯度，样本数多的时候，导致计算量大增，所以实际生产环境中，往往采用随机梯度下降算法（Stochastic Gradient Descent），一般简写做SGD。

SGD每次迭代的时候均匀随机得选择一个样本或者mini-batch做更新：

$\mathbf{w}_{t+1} = \mathbf{w}_t - \eta \triangledown f_i(\mathbf{w}_t)$

相对于梯度下降，SGD的好处非常明显，就是可以减少每次更新的计算代价，但是SGD带来的问题是收敛速度不如梯度下降（收敛速度是衡量优化算法计算复杂度的基本工具，具体定义可以参考https://en.wikipedia.org/wiki/Rate_of_convergence 或者其他优化相关的教材），也就是说为了达到同样的精度，SGD需要的总迭代次数要大于梯度下降，但是，单次迭代的计算量要小得多。从收敛速度分析上看，SGD能够在目标函数强凸并且递减步长的情况下做到 $O(1/T)$ 的次线性收敛（sublinear convergence），而梯度下降则可以在目标函数强凸的情况下做到 $O(\rho^T)$ ( $\rho < 1$ ) 的线性收敛（linear convergence）。总结起来就是，如果想快速得到一个可以勉强接受的解，SGD比梯度下降更加合适，但是如果想得到一个精确度高的解，应当选择梯度下降。

SGD后来后来也衍生出了非常多的变种，尤其是一类分析regret的online算法，包括Adagrad、Dual Averaging、FTRL等。但是，始终学术界对于SGD还有一种期待，就是：是否可以把SGD做到和梯度下降一样的线性收敛。直到2012和2013年，SAG[1]与SVRG[2]算法发表在NIPS上，成为近几年SGD类算法的最大突破。

SAG算法（算法框图摘自[4]，这里的 $f_i'(.)$ 是指梯度函数 $\triangledown f_i(.)$ ，而 $x$ 是指上文中的优化参数 $\mathbf{w}$ ）

作者：li Eta
链接：https://zhuanlan.zhihu.com/p/22402784
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

SAG算法在内存中为每个样本都维护一个旧的梯度 $y_i$ ，随机选择一个样本 $i$ 来更新 $d$ ，并用 $d$ 来更新参数 $x$ 。具体得说，更新的项 $d$ 来自于用新的梯度 $f_i'(x)$ 替换掉 $d$ 中的旧梯度 $y_i$ ，这也就是 $d = d - y_i + f_i'(x)$ 表达的意思。如此，每次更新的时候仅仅需要计算一个样本的梯度，而不是所有样本的梯度。计算开销与SGD无异，但是内存开销要大得多。[1]中已经证明SAG是一种线性收敛算法，这个速度远比SGD快。

SAG实验结果（结果摘自[1]的arxiv长文版）

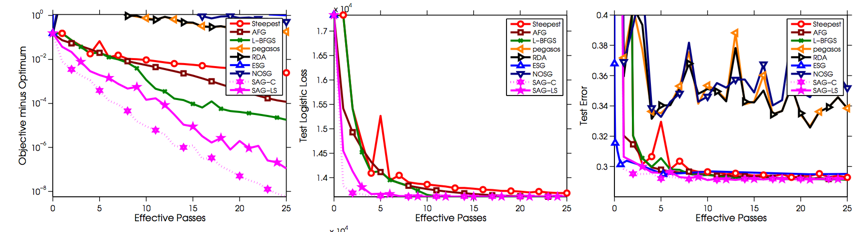
实验目标函数是l2-regularized logistic regression，左一是训练误差，左二和左三分别是两种测试目标函数与测试误差。注意左一的纵坐标是对数坐标，一般衡量优化算法的速度都会采用对数坐标，因为在对数坐标中可以明显看出一个算法是线性收敛（近乎直线下降）还是次线性收敛（大体是一条向下凸的曲线）。可以看出SAG是一种线性收敛算法，且相对于其他参与比较的算法有很大的优势。具体实验配置数据集等可以参考原文。

SVRG算法（算法摘自[2]，这里的 $\psi$ 就是上文中的损失函数 $f$ ）

SVRG的算法思路是，每过一段时间计算一次所有样本的梯度 $\tilde{\mu}$ ，每个阶段内部的单次更新采用 $\triangledown \psi_{i_t} (w_{t-1}) - \triangledown \psi_{i_t} (\tilde{w}) + \tilde{\mu}$ 来更新当前参数，每次更新最多计算两次梯度。相对于SAG来说，不需要在内存中为每个样本都维护一个梯度，也就是说节省了内存资源。此外，SVRG中提出了一个非常重要的概念叫做variance reduction（方差缩减），这个概念需要联系SGD的收敛性分析来理解，在SGD的收敛性分析中需要假设样本梯度的的方差是有常数上界的，然而正是因为这个常数上界导致了SGD无法线性收敛，因此SVRG的收敛性分析中利用 $\triangledown \psi_{i_t} (w_{t-1}) - \triangledown \psi_{i_t} (\tilde{w}) + \tilde{\mu}$ 这种特殊的更新项来让方差有一个可以不断减少的上界，因此也就做到了线性收敛，这一点就是SVRG的核心，SAG的策略其实也与此类似（虽然证明过程不同）。

SVRG实验结果（结果摘自[2]）

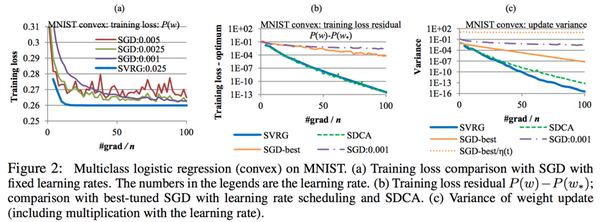
上图为SVRG在凸的logistic regression上的表现，注意左一纵坐标是训练误差，左二左三纵坐标是对数坐标，实验中可以看出SVRG显然是线性收敛算法，相对于SGD有非常大的优势，和SDCA具备同阶的速度。

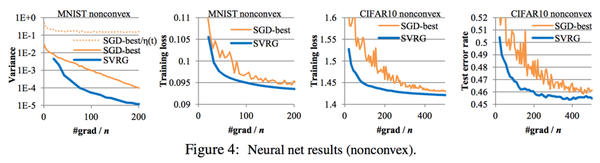
上图为SVRG在非凸的神经网络（Neural Network或称作Deep Learning）上的表现（原文中是在单隐层神经网络上做的实验）。一定程度上说明，SVRG在NN上也可以发挥很好的作用。

后来这类线性收敛的随机优化算法陆续出现了很多变种，比如SAGA算法[3]。

参考文献：

Roux, Nicolas L., Mark Schmidt, and Francis R. Bach. "A stochastic gradient method with an exponential convergence rate for finite training sets."Advances in Neural Information Processing Systems. 2012.
Johnson, Rie, and Tong Zhang. "Accelerating stochastic gradient descent using predictive variance reduction."Advances in Neural Information Processing Systems. 2013.
Defazio, Aaron, Francis Bach, and Simon Lacoste-Julien. "Saga: A fast incremental gradient method with support for non-strongly convex composite objectives."Advances in Neural Information Processing Systems. 2014.
Schmidt, Mark, Nicolas Le Roux, and Francis Bach. "Minimizing finite sums with the stochastic average gradient."arXiv preprint arXiv:1309.2388 (2013).

补充：

梯度下降法大家族（BGD，SGD，MBGD）

批量梯度下降法（Batch Gradient Descent）

　　　　批量梯度下降法，是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新

随机梯度下降法（Stochastic Gradient Descent）

　　　　随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本j来求梯度。

　　　　随机梯度下降法，和批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

小批量梯度下降法（Mini-batch Gradient Descent）

　　小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷，也就是对于m个样本，我们采用x个样子来迭代，1<x<m。一般可以取x=10，当然根据样本的数据，可以调整这个x的值。

梯度下降法和其他无约束优化算法的比较

　　　　在机器学习中的无约束优化算法，除了梯度下降以外，还有前面提到的最小二乘法，此外还有牛顿法和拟牛顿法。

　　　　梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。

　　　　梯度下降法和牛顿法/拟牛顿法相比，两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言，使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。

0 0