凸包聚类

QuickHull

From Wikipedia, the free encyclopedia

Main article: Convex hull algorithms

QuickHull is a method of computing the convex hull of a finite set of points in the plane. It uses a divide and conquer approach similar to that of QuickSort, which its name derives from. Its average case complexity is considered to be O(n * log(n)), whereas in the worst case it takes O(n²) (quadratic).

Algorithm[edit]

Steps 1-2: Divide points in two subsets

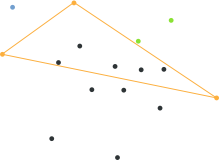
Under average circumstances the algorithm works quite well, but processing usually becomes slow in cases of high symmetry or points lying on the circumference of a circle. The algorithm can be broken down to the following steps:

1. Find the points with minimum and maximum x coordinates, those are bound to be part of the convex.
2. Use the line formed by the two points to divide the set in two subsets of points, which will be processed recursively.
3. Determine the point, on one side of the line, with the maximum distance from the line. The two points found before along with this one form a triangle.
4. The points lying inside of that triangle cannot be part of the convex hull and can therefore be ignored in the next steps.
5. Repeat the previous two steps on the two lines formed by the triangle (not the initial line).
6. Keep on doing so on until no more points are left, the recursion has come to an end and the points selected constitute the convex hull.

Steps 3-5: Find maximal distance point, ignore points inside triangle and repeat it

Step 6: Recurse until no more points are left

References[edit]

• Barber, C. Bradford; Dobkin, David P.; Huhdanpaa, Hannu (1 December 1996). “The quickhull algorithm for convex hulls”.ACM Transactions on Mathematical Software 22 (4): 469–483. doi:10.1145/235815.235821.

来源：http://en.wikipedia.org/wiki/QuickHull

——————————-

其他算法（但不一定适用于N维）：

Algorithms[edit]

Known convex hull algorithms are listed below, ordered by the date of first publication. Time complexity of each algorithm is stated in terms of the number of inputs points n and the number of points on the hull h. Note that in the worst case h may be as large as n.

• Gift wrapping aka Jarvis march — O(nh)
  One of the simplest (although not the most time efficient in the worst case) planar algorithms. Discovered independently by Chand & Kapur in 1970 and R. A. Jarvis in 1973. It has O(nh) time complexity, where n is the number of points in the set, and h is the number of points in the hull. In the worst case the complexity is Θ(n²).

• Graham scan — O(n log n)
  A slightly more sophisticated, but much more efficient algorithm, published by Ronald Graham in 1972. If the points are already sorted by one of the coordinates or by the angle to a fixed vector, then the algorithm takes O(n) time.

• QuickHull
  Discovered independently in 1977 by W. Eddy and in 1978 by A. Bykat. Just like the quicksort algorithm, it has the expected time complexity of O(n log n), but may degenerate to Θ(nh) = O(n²) in the worst case.

• Divide and conquer — O(n log n)
  Another O(n log n) algorithm, published in 1977 by Preparata and Hong. This algorithm is also applicable to the three dimensional case.

• Monotone chain aka Andrew’s algorithm— O(n log n)
  Published in 1979 by A. M. Andrew. The algorithm can be seen as a variant of Graham scan which sorts the points lexicographically by their coordinates. When the input is already sorted, the algorithm takes O(n) time.

• Incremental convex hull algorithm — O(n log n)
  Published in 1984 by Michael Kallay.

• The ultimate planar convex hull algorithm — O(n log h)
  The first optimal output-sensitive algorithm, it uses the technique of marriage-before-conquest. Published by Kirkpatrick and Seidel in 1986.

• Chan’s algorithm — O(n log h)
  A simpler optimal output-sensitive algorithm discovered by Chan in 1996.

在线获取convex hull算法：

On-line and dynamic convex hull problems[edit]

The discussion above considers the case when all input points are known in advance. One may consider two other settings.^[1]

• Online convex hull problem: Input points are obtained sequentially one by one. After each point arrives on input, the convex hull for the pointset obtained so far must be efficiently computed.
• Dynamic convex hull maintenance: The input points may be sequentially inserted or deleted, and the convex hull must be updated after each insert/delete operation.

Insertion of a point may increase the number of vertices of a convex hull at most by 1, while deletion may convert a 3-vertex convex hull into an n-1-vertex one.

The online version may be handled with O(log n) per point, which is asymptotically optimal. The dynamic version may be handled with O(log² n) per operation.^[1]

来源：http://en.wikipedia.org/wiki/Convex_hull_algorithms

注：Matlab中计算N维点集的凸包函数名为convhulln delaunayn griddatan voronoin.