强化学习入门 第五讲 值函数逼近

转载自 知乎专栏 天津包子馅儿的知乎

前面已经讲了强化学习的基本方法：基于动态规划的方法，基于蒙特卡罗的方法和基于时间差分的方法。这些方法有一个基本的前提条件，那就是状态空间和动作空间是离散的，而且状态空间和动作空间不能太大。

我们回想一下已经介绍的强化学习方法的基本步骤是：首先评估值函数，接着利用值函数改进当前的策略。其中值函数的评估是关键。

对于模型已知的系统，值函数可以利用动态规划的方法得到；对于模型未知的系统，可以利用蒙特卡罗的方法或者时间差分的方法得到。

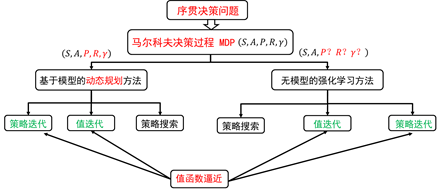
注意，这时的值函数其实是一个表格。对于状态值函数，其索引是状态；对于行为值函数，其索引是状态-行为对。值函数迭代更新的过程实际上就是对这张表进行迭代更新。因此，之前讲的强化学习算法又称为表格型强化学习。对于状态值函数，其表格的维数为状态的个数 ，其中 为状态空间。若状态空间的维数很大，或者状态空间为连续空间，此时值函数无法用一张表格来表示。这时，我们需要利用函数逼近的方法对值函数进行表示。如图5.1所示。当值函数利用函数逼近的方法表示后，可以利用策略迭代和值迭代方法构建强化学习算法。

图5.1 强化学习分类

在表格型强化学习中，值函数对应着一张表。在值函数逼近方法中，值函数对应着一个逼近函数 。从数学角度来看，函数逼近方法可以分为参数逼近和非参数逼近，因此强化学习值函数估计可以分为参数化逼近和非参数化逼近。其中参数化逼近又分为线性参数化逼近和非线性化参数逼近。

这一节，我们主要介绍参数化逼近。所谓参数化逼近，是指值函数可以由一组参数 来近似。我们将逼近的值函数写为：。

当逼近的值函数结构确定时，（如线性逼近时选定了基函数，非线性逼近时选定了神经网络的结构），那么值函数的逼近就等价于参数的逼近。值函数的更新也就等价于参数的更新。也就是说，我们需要利用试验数据来更新参数值。如何利用数据更新参数值呢？也就是说如何从数据中学到参数值呢？

我们回顾一下表格型强化学习值函数更新的公式，以便从中得到启发：

蒙特卡罗方法，值函数更新公式为：

 (5.1) 

TD方法值函数更新公式为：

 (5.2)

方法值函数更新公式为：

 (5.3)

从式（5.1）—（5.3）值函数的更新过程我们看到，值函数更新过程是向着目标值函数靠近。

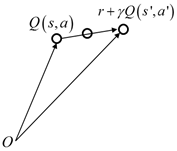
如图5.2所示为TD方法更新值函数的过程。

图5.2 TD方法值函数更新

从表格型值函数的更新过程，我们不难总结出不管是蒙特卡罗方法还是TD方法，都是朝着一个目标值更新的，这个目标值在蒙特卡罗方法中是 ，在TD方法中是 ，在中是 。

将表格型强化学习值函数的更新过程推广到值函数逼近过程，有如下形式：

函数逼近 的过程是一个监督学习的过程，其数据和标签对为：, 其中
等价于蒙特卡罗方法中的，TD方法中的  ，以及  中的 。

训练的目标函数为：

 (5.4)

现在我们比较一下表格型强化学习和函数逼近方法的强化学习值函数更新时的异同点：

（1） 表格型强化学习进行值函数更新时，只有当前状态处的值函数在改变，其他地方的值函数不发生改变。

（2） 值函数逼近方法进行值函数更新时，因此更新的是参数，而估计的值函数为，所以当参数发生改变时，任意状态处的值函数都会发生改变。

值函数更新可分为增量式学习方法和批学习方法。我们先介绍增量式学习方法。随机梯度下降法是最常用的增量式学习方法。

由（5.4）我们得到参数的随机梯度更新为：

 (5.5)

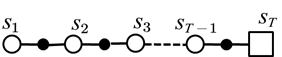
基于蒙特卡罗方法的函数逼近，具体的过程为：

给定要评估的策略，产生一次试验：

值函数的更新过程实际是一个监督学习的过程，其中监督数据集从蒙塔卡罗的试验中得到，其数据集为：,

值函数的更新：

 (5.6)

其中值比较小。在随机梯度下降法中，似乎并不清楚为什么每一步采用很小的更新。难道我们不能在梯度的方向上移动很大的距离甚至完全消除误差吗？在很多情况下确实可以这样做，但是通常这并不是我们想要的。请记住，我们的目的并不是在所有的状态找到精确的值函数，而是一个能平衡所有不同状态误差的值函数逼近。如果我们在一步中完全纠正了偏差，那么我们就无法找到这样的一个平衡了。因此值取得比较小可以维持这种平衡。

图5.3 基于梯度的蒙特卡罗值函数逼近

如图5.3所示为基于梯度的蒙塔卡罗值函数逼近更新过程。蒙特卡罗方法的目标值函数使用一次试验的整个回报返回值，我们再看下时间差分方法。根据方程（5.5），TD(0)方法中目标值函数为： ，即目标值函数用到了bootstrapping的方法。此时，我们注意到此时要更新的参数 不仅出现在要估计的值函数 中，还出现在目标值函数中。若只考虑参数 对估计值函数 的影响而忽略对目标值函数的影响，这种方法并非完全的梯度法，只有部分梯度，因此称为半梯度法：

 (5.7)

图5.4 基于半梯度的TD(0)值函数评估算法

如图5.4所示为基于半梯度的TD(0)值函数评估算法。

图5.5 基于半梯度的Sarsa算法

如图5.5为基于半梯度的Sarsa算法。与表格型强化学习相比，值函数逼近方法中对值函数的更新换成了对参数的更新，参数的学习过程为监督学习。

到目前为止，我们还没有讨论要逼近的值函数的形式。值函数可以采用线性逼近也可以采用非线性逼近。非线性逼近常用的是神经网络。

下面我们仅讨论线性逼近：

相比于非线性逼近，线性逼近的好处是只有一个最优值，因此可以收敛到全局最优。其中为状态s处的特征函数，或者称为基函数。

常用的基函数的类型为：

多项式基函数，如。

傅里叶基函数，

径向基函数：

将线性逼近值函数带入随机梯度下降法和半梯度下降法中，可以得到参数的更新公式，如下：

蒙特卡罗方法值函数更新为：

TD(0)线性逼近值函数更新为：

正向视角的更新为：

后向视角的更新为：

前面讨论的是增量式方法更新。增量式方法参数更新过程随机性比较大，尽管计算简单，但样本数据的利用效率并不高。而批的方法，尽管计算复杂，但计算效率高。

所谓批的方法是指给定经验数据集，找到最好的拟合函数，使得：最小可利用线性最小二乘逼近：

最小二乘蒙特卡罗方法参数为：

最小二乘差分方法为：

最小二乘方法为：