最小二乘和梯度下降

最近一个月都在学习最小二乘和梯度下降，Python也是刚入门，整理了几篇Blog，总结了一下这两个线性优化算法。区别主要有:

最小二乘法的目标：求误差的最小平方和，对应有两种：线性和非线性。线性最小二乘的解是closed-form即，而非线性最小二乘没有closed-form，通常用迭代法求解。

迭代法，即在每一步update未知量逐渐逼近解，可以用于各种各样的问题（包括最小二乘），比如求的不是误差的最小平方和而是最小立方和。

梯度下降是迭代法的一种，可以用于求解最小二乘问题（线性和非线性都可以）。高斯-牛顿法是另一种经常用于求解非线性最小二乘的迭代法（一定程度上可视为标准非线性最小二乘求解方法）。

还有一种叫做Levenberg-Marquardt的迭代法用于求解非线性最小二乘问题，就结合了梯度下降和高斯-牛顿法。

所以如果把最小二乘看做是优化问题的话，那么梯度下降是求解方法的一种，是求解线性最小二乘的一种，高斯-牛顿法和Levenberg-Marquardt则能用于求解非线性最小二乘。

回归与梯度下降：

回归在数学上来说是给定一个点集，能够用一条曲线去拟合之，如果这个曲线是一条直线，那就被称为线性回归，如果曲线是一条二次曲线，就被称为二次回归，回归还有很多的变种，如locally weighted回归，logistic回归，等等，这个将在后面去讲。

用一个很简单的例子来说明回归，这个例子来自很多的地方，也在很多的open source的软件中看到，比如说weka。大概就是，做一个房屋价值的评估系统，一个房屋的价值来自很多地方，比如说面积、房间的数量（几室几厅）、地 段、朝向等等，这些影响房屋价值的变量被称为特征(feature)，feature在机器学习中是一个很重要的概念，有很多的论文专门探讨这个东西。在 此处，为了简单，假设我们的房屋就是一个变量影响的，就是房屋的面积。

假设有一个房屋销售的数据如下：

面积(m^2)  销售价钱（万元）

123            250

150            320

87              160

102            220

…               …

这个表类似于帝都5环左右的房屋价钱，我们可以做出一个图，x轴是房屋的面积。y轴是房屋的售价，如下：

如果来了一个新的面积，假设在销售价钱的记录中没有的，我们怎么办呢？

我们可以用一条曲线去尽量准的拟合这些数据，然后如果有新的输入过来，我们可以在将曲线上这个点对应的值返回。如果用一条直线去拟合，可能是下面的样子：

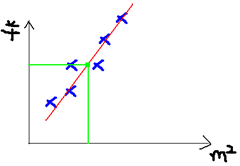
绿色的点就是我们想要预测的点。

首先给出一些概念和常用的符号，在不同的机器学习书籍中可能有一定的差别。

房屋销售记录表 - 训练集(training set)或者训练数据(training data), 是我们流程中的输入数据，一般称为x

房屋销售价钱 - 输出数据，一般称为y

拟合的函数（或者称为假设或者模型），一般写做 y = h(x)

训练数据的条目数(#training set), 一条训练数据是由一对输入数据和输出数据组成的

输入数据的维度(特征的个数，#features)，n

下面是一个典型的机器学习的过程，首先给出一个输入数据，我们的算法会通过一系列的过程得到一个估计的函数，这个函数有能力对没有见过的新数据给出一个新的估计，也被称为构建一个模型。就如同上面的线性回归函数。

我们用X1，X2..Xn 去描述feature里面的分量，比如x1=房间的面积，x2=房间的朝向，等等，我们可以做出一个估计函数：

θ在这儿称为参数，在这儿的意思是调整feature中每个分量的影响力，就是到底是房屋的面积更重要还是房屋的地段更重要。为了如果我们令X0 = 1，就可以用向量的方式来表示了：

我们程序也需要一个机制去评估我们θ是否比较好，所以说需要对我们做出的h函数进行评估，一般这个函数称为损失函数（loss function）或者错误函数(error function)，描述h函数不好的程度，在下面，我们称这个函数为J函数

在这儿我们可以做出下面的一个错误函数：

这个错误估计函数是去对x(i)的估计值与真实值y(i)差的平方和作为错误估计函数，前面乘上的1/2是为了在求导的时候，这个系数就不见了。

如何调整θ以使得J(θ)取得最小值有很多方法，其中有最小二乘法(min square)，是一种完全是数学描述的方法，还有一种就是梯度下降。

我们先看看最小二乘的矩阵求解过程：

最小二乘法是一种数据拟合方法，我们从矩阵的角度来理解： 

首先我们给出一个矩阵中的定义： 

R(A)={Ax|x∈Rn},A∈Rn×n

有了上面的定义之后，我们就可以写出最小二乘问题的矩阵形式： 

∃b∉R(A),b∈Rn,minx∈Rn∥Ax−b∥2

用bi格高一点的说法来说，就是求在欧几里得空间中以2-范数作为距离，使得向量Ax与b之间距离最小的x。 
我们的目标是求： 

minx∈Rn∥Ax−b∥2

当然我们知道，使得距离最小的向量x与使得距离平方最小的向量x是相同的，于是我们可以将所求的目标改写为： 

minx∈Rn∥Ax−b∥22

结合一些矩阵、行列式的知识，我们知道： 

∥Ax−b∥22=(Ax−b)T∗(Ax−b)

根据我们大一学过的高数知识，我们知道，求最极值问题直接对应的就是导数为零，因此我们试图将所给出的原式的矩阵形式求导：

不过首先我们需要补充矩阵微积分(matrix calculus)的一些知识 
(PS:是矩阵微积分吧…我没有翻译错吧….) 

∂xTa∂x=∂aTx∂x=a

∂xTAx∂x=Ax+ATx

如果矩阵A是对称的(symmetric matrix): 

Ax+ATx=2Ax

接下来，我们对原式化简并求其对x的导数： 

∥Ax−b∥22=xTATAx−bTAx−xTATb+bTb

求导得到： 

∂∥Ax−b∥22∂x=2ATAx−2ATb=0

于是我们就得到了，最小二乘法解的矩阵形式： 

x=(ATA)−1ATb

代码实现如下：

#coding=utf-8import numpy as npimport matplotlib.pyplot as plt#读取训练集def loadDataSet(fileName):    numFeat = len(open(fileName).readline().split('\t')) - 1    dataMat = []; labelMat = []    fr = open(fileName)    for line in fr.readlines():        lineArr =[]        curLine = line.strip().split('\t')        for i in range(numFeat):            lineArr.append(float(curLine[i]))        dataMat.append(lineArr)        labelMat.append(float(curLine[-1]))    return dataMat,labelMat#最小二乘矩阵方法def LS(xArr,yArr):    xMat = np.mat(xArr); yMat = np.mat(yArr).T    xTx = xMat.T*xMat    if np.linalg.det(xTx) == 0.0:        print "cannot do inverse"        return    ws = xTx.I * (xMat.T*yMat)    return wsxArr,yArr = loadDataSet('ex0.txt')ws = LS(xArr,yArr)xMat = np.mat(xArr)xCopy = xMat.copy()xCopy.sort(0)yMat = np.mat(yArr)yHat = xCopy * ws#画图fig = plt.figure()ax1 = fig.add_subplot(111)plt.xlabel('X')plt.ylabel('Y')ax1.scatter(xCopy[:,1],yHat)ax2 = fig.add_subplot(111)ax2.scatter(xMat[:,1],yMat)plt.show()

现在再来看看梯度下降法的流程：

1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。

2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。

为了更清楚，给出下面的图：

 这是一个表示参数θ与误差函数J(θ)的关系图，红色的部分是表示J(θ)有着比较高的取值，我们需要的是，能够让J(θ)的值尽量的低。也就是深蓝色的部分。θ0，θ1表示θ向量的两个维度。

在上面提到梯度下降法的第一步是给θ给一个初值，假设随机给的初值是在图上的十字点。

然后我们将θ按照梯度下降的方向进行调整，就会使得J(θ)往更低的方向进行变化，如图所示，算法的结束将是在θ下降到无法继续下降为止。

 当然，可能梯度下降的最终点并非是全局最小点，可能是一个局部最小点，可能是下面的情况：

上面这张图就是描述的一个局部最小点，这是我们重新选择了一个初始点得到的，看来我们这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点

下面我将用一个例子描述一下梯度减少的过程，对于我们的函数J(θ)求偏导J：（求导的过程如果不明白，可以温习一下微积分）

下面是更新的过程，也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值，-后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。

 一个很重要的地方值得注意的是，梯度是有方向的，对于一个向量θ，每一维分量θi都可以求出一个梯度的方向，我们就可以找到一个整体的方向，在变化的时候，我们就朝着下降最多的方向进行变化就可以达到一个最小点，不管它是局部的还是全局的。

用更简单的数学语言进行描述步骤2）是这样的：

 

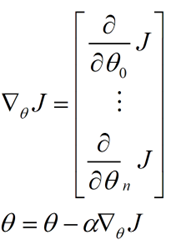
梯度下降法的类型

基于如何使用数据计算代价函数的导数，梯度下降法可以被定义为不同的形式（various variants）。确切地说，根据使用数据量的大小（the amount of data），时间复杂度（time complexity）和算法的准确率（accuracy of the algorithm），梯度下降法可分为：

1.       批量梯度下降法（Batch Gradient Descent, BGD）；

2.       随机梯度下降法（Stochastic Gradient Descent, SGD）；

3.       小批量梯度下降法（Mini-Batch Gradient Descent, MBGD）。

批量梯度下降法原理

      这是梯度下降法的基本类型，这种方法使用整个数据集（the complete dataset）去计算代价函数的梯度。每次使用全部数据计算梯度去更新参数，批量梯度下降法会很慢，并且很难处理不能载入内存（don’t fit in memory）的数据集。在随机初始化参数后，按如下方式计算代价函数的梯度：

 

其中，m是训练样本（training examples）的数量。

Note:

     1. 如果训练集有3亿条数据，你需要从硬盘读取全部数据到内存中；

     2. 每次一次计算完求和后，就进行参数更新；

     3.  然后重复上面每一步；

     4. 这意味着需要较长的时间才能收敛；

     5. 特别是因为磁盘输入/输出（disk I/O）是系统典型瓶颈，所以这种方法会不可避免地需要大量的读取。

上图是每次迭代后的等高线图，每个不同颜色的线表示代价函数不同的值。运用梯度下降会快速收敛到圆心，即唯一的一个全局最小值。批量梯度下降法不适合大数据集。

随机梯度下降法原理

   批量梯度下降法被证明是一个较慢的算法，所以，我们可以选择随机梯度下降法达到更快的计算。随机梯度下降法的第一步是随机化整个数据集。在每次迭代仅选择一个训练样本去计算代价函数的梯度，然后更新参数。即使是大规模数据集，随机梯度下降法也会很快收敛。随机梯度下降法得到结果的准确性可能不会是最好的，但是计算结果的速度很快。在随机化初始参数之后，使用如下方法计算代价函数的梯度：

这里m表示训练样本的数量。

如下为随机梯度下降法的伪码：

       1. 进入内循环（inner loop）;

       2. 第一步：挑选第一个训练样本并更新参数，然后使用第二个实例；

       3. 第二步：选第二个训练样本，继续更新参数；

       4. 然后进行第三步…直到第n步；

       5. 直到达到全局最小值

如下图所示，随机梯度下降法不像批量梯度下降法那样收敛，而是游走到接近全局最小值的区域终止。

 

小批量梯度下降法原理

 小批量梯度下降法是最广泛使用的一种算法，该算法每次使用m个训练样本（称之为一批）进行训练，能够更快得出准确的答案。小批量梯度下降法不是使用完整数据集，在每次迭代中仅使用m个训练样本去计算代价函数的梯度。一般小批量梯度下降法所选取的样本数量在50到256个之间，视具体应用而定。

1.这种方法减少了参数更新时的变化，能够更加稳定地收敛。

2.同时，也能利用高度优化的矩阵，进行高效的梯度计算。

随机初始化参数后，按如下伪码计算代价函数的梯度：

这里b表示一批训练样本的个数，m是训练样本的总数。

 

Notes:

1. 实现该算法时，同时更新参数。

2. 学习速率α（也称之为步长）。如果α过大，算法可能不会收敛；如果α比较小，就会很容易收敛。

3. 检查梯度下降法的工作过程。画出迭代次数与每次迭代后代价函数值的关系图，这能够帮助你了解梯度下降法是否取得了好的效果。每次迭代后J(θ)应该降低，多次迭代后应该趋于收敛。

4. 不同的学习速率在梯度下降法中的效果

代码实现如下：

# -*- coding: utf-8 -*-from __future__ import division     #精准除法import numpy as npimport matplotlib.pyplot as plt#读取文本文件def loadDataSet(fileName):    numFeat = len(open(fileName).readline().split('\t')) - 1    dataMat = []; labelMat = []    fr = open(fileName)    for line in fr.readlines():        lineArr =[]        curLine = line.strip().split('\t')        for i in range(numFeat):            lineArr.append(float(curLine[i]))        dataMat.append(lineArr)        labelMat.append(float(curLine[-1]))    return dataMat,labelMat#批量低度下降，调用所有样本def BGD(x,y):    epsilon = 0.0001    alpha = 0.05    loss = [0, 0]    error0 = 0    m = len(x)    theta0 = 0                                                              #初始化参数    theta1 = 0    for i in range(m):        loss[0] = (theta0 + theta1 * x[i][1] - y[i])                        #计算残差        theta0 -= alpha * loss[0] * x[i][0]                                 #梯度 = loss[0] * x[i][j]        theta1 -= alpha * loss[0] * x[i][1]    error1 = 0                                                              #计算损失函数    for j in range(len(x)):        error1 += (y[j] - (theta0 + theta1 * x[j][1])) ** 2 / m        if abs(error1 - error0) < epsilon:            break        else:            error0 = error1    return theta0 , theta1 ,error1#随机梯度下降def SGD(x,y):    epsilon = 0.0001    alpha = 0.05    loss = [0, 0]    error0 = 0    m = len(x)    theta0 = 0                                                              #初始化参数    theta1 = 0    for i in range(m):        np.random.shuffle(x)                                                #随机化测试集，不返回任何值        loss[0] = (theta0 + theta1 * x[i][1] - y[i])                        #计算残差        theta0 -= alpha * loss[0] * x[-1][0]                                 #梯度 = loss[0] * x[i][j]        theta1 -= alpha * loss[0] * x[-1][1]    error1 = 0                                                              #计算损失函数    for j in range(len(x)):        error1 += (y[j] - (theta0 + theta1 * x[j][1])) ** 2 / 2        if abs(error1 - error0) < epsilon:            break        else:            error0 = error1    return theta0 , theta1 ,error1#小批量梯度下降，每次迭代只采用max_iter个样本def MBGD(x,y):    epsilon = 0.0001    alpha = 0.05    loss = [0, 0]    error0 = 0    theta0 = 0                                                              #初始化参数    theta1 = 0    max_iter = 50                                                           #选取样本数量    m = np.arange(len(x))    for i in range(max_iter):        m = np.random.permutation(m)                                        #返回一个随机后的值    for i in m:                                                             #i在随机序列m中循环        loss[0] = (theta0 + theta1 * x[i][1] - y[i])                        #计算残差        theta0 -= alpha * loss[0] * x[i][0]                                 #梯度 = loss[0] * x[i][j]        theta1 -= alpha * loss[0] * x[i][1]    error1 = 0                                                              #计算损失函数    for j in range(len(x)):        error1 += (y[j] - (theta0 + theta1 * x[j][1])) ** 2 / 2        if abs(error1 - error0) < epsilon:            break        else:            error0 = error1    return theta0 , theta1 ,error1#导入测试集x,y =loadDataSet('ex0.txt')theta0, theta1, error1 = BGD(x,y)print ' The：theta0 : %f, theta1 : %f, error1 : %f' % (theta0, theta1, error1)#预测图像xMat = np.mat(x)yMat = np.mat(y)yHat = xMat*theta1 + theta0#打印图像fig = plt.figure()ax1 = fig.add_subplot(111)plt.xlabel('X')plt.ylabel('Y')ax1.scatter(xMat[:,1],yMat)ax2 = fig.add_subplot(111)ax2.scatter(xMat,yHat)plt.show()

梯度下降优化算法：

下面，我们将列举一些算法，这些算法被深度学习社区广泛用来处理前面提到的挑战。我们不会讨论在实际中不适合在高维数据集中计算的算法，例如诸如牛顿法的二阶方法。

4.1 动量法

SGD很难通过陡谷，即在一个维度上的表面弯曲程度远大于其他维度的区域[19]，这种情况通常出现在局部最优点附近。在这种情况下，SGD摇摆地通过陡谷的斜坡，同时，沿着底部到局部最优点的路径上只是缓慢地前进，这个过程如图2a所示。

 
图2：来源：Genevieve B. Orr 

如图2b所示，动量法[16]是一种帮助SGD在相关方向上加速并抑制摇摆的一种方法。动量法将历史步长的更新向量的一个分量γ增加到当前的更新向量中（部分实现中交换了公式中的符号）

vt=γvt−1+η∇θJ(θ)

θ=θ−vt

动量项γ通常设置为0.9或者类似的值。

从本质上说，动量法，就像我们从山上推下一个球，球在滚下来的过程中累积动量，变得越来越快（直到达到终极速度，如果有空气阻力的存在，则γ<1）。同样的事情也发生在参数的更新过程中：对于在梯度点处具有相同的方向的维度，其动量项增大，对于在梯度点处改变方向的维度，其动量项减小。因此，我们可以得到更快的收敛速度，同时可以减少摇摆。

4.2 Nesterov加速梯度下降法

然而，球从山上滚下的时候，盲目地沿着斜率方向，往往并不能令人满意。我们希望有一个智能的球，这个球能够知道它将要去哪，以至于在重新遇到斜率上升时能够知道减速。

Nesterov加速梯度下降法（Nesterov accelerated gradient，NAG）[13]是一种能够给动量项这样的预知能力的方法。我们知道，我们利用动量项γvt−1来更新参数θ。通过计算θ−γvt−1能够告诉我们参数未来位置的一个近似值（梯度并不是完全更新），这也就是告诉我们参数大致将变为多少。通过计算关于参数未来的近似位置的梯度，而不是关于当前的参数θ的梯度，我们可以高效的求解 ：

vt=γvt−1+η∇θJ(θ−γvt−1)

θ=θ−vt

同时，我们设置动量项γ大约为0.9。动量法首先计算当前的梯度值（图3中的小的蓝色向量），然后在更新的累积梯度（大的蓝色向量）方向上前进一大步，Nesterov加速梯度下降法NAG首先在先前累积梯度（棕色的向量）方向上前进一大步，计算梯度值，然后做一个修正（绿色的向量）。这个具有预见性的更新防止我们前进得太快，同时增强了算法的响应能力，这一点在很多的任务中对于RNN的性能提升有着重要的意义[2]。

 
图3：Nesterov更新（来源：G. Hinton的课程6c） 

对于NAG的直观理解的另一种解释可以参见http://cs231n.github.io/neural-networks-3/，同时Ilya Sutskever在其博士论文[18]中给出更详细的综述。

既然我们能够使得我们的更新适应误差函数的斜率以相应地加速SGD，我们同样也想要使得我们的更新能够适应每一个单独参数，以根据每个参数的重要性决定大的或者小的更新。

4.3 Adagrad

Adagrad[7]是这样的一种基于梯度的优化算法：让学习率适应参数，对于出现次数较少的特征，我们对其采用更大的学习率，对于出现次数较多的特征，我们对其采用较小的学习率。因此，Adagrad非常适合处理稀疏数据。Dean等人[6]发现Adagrad能够极大提高了SGD的鲁棒性并将其应用于Google的大规模神经网络的训练，其中包含了YouTube视频中的猫的识别。此外，Pennington等人[15]利用Adagrad训练Glove词向量，因为低频词比高频词需要更大的步长。

前面，我们每次更新所有的参数θ时，每一个参数θi都使用的是相同的学习率η。由于Adagrad在t时刻对每一个参数θi使用了不同的学习率，我们首先介绍Adagrad对每一个参数的更新，然后我们对其向量化。为了简洁，令gt,i为在t时刻目标函数关于参数θi的梯度：

gt,i=∇θJ(θi)

在t时刻，对每个参数θi的更新过程变为：

θt+1,i=θt,i−η⋅gt,i

对于上述的更新规则，在t时刻，基于对θi计算过的历史梯度，Adagrad修正了对每一个参数θi的学习率：

θt+1,i=θt,i−ηGt,ii+ϵ−−−−−−−√⋅gt,i

其中，Gt∈Rd×d是一个对角矩阵，对角线上的元素i,i是直到t时刻为止，所有关于θi的梯度的平方和（Duchi等人[7]将该矩阵作为包含所有先前梯度的外积的完整矩阵的替代，因为即使是对于中等数量的参数d，矩阵的均方根的计算都是不切实际的。），ϵ是平滑项，用于防止除数为0（通常大约设置为1e−8）。比较有意思的是，如果没有平方根的操作，算法的效果会变得很差。

由于Gt的对角线上包含了关于所有参数θ的历史梯度的平方和，现在，我们可以通过Gt和gt之间的元素向量乘法⊙向量化上述的操作：

θt+1=θt−ηGt+ϵ−−−−−√⊙gt

Adagrad算法的一个主要优点是无需手动调整学习率。在大多数的应用场景中，通常采用常数0.01。

Adagrad的一个主要缺点是它在分母中累加梯度的平方：由于没增加一个正项，在整个训练过程中，累加的和会持续增长。这会导致学习率变小以至于最终变得无限小，在学习率无限小时，Adagrad算法将无法取得额外的信息。接下来的算法旨在解决这个不足。

4.4 Adadelta

Adadelta[21]是Adagrad的一种扩展算法，以处理Adagrad学习速率单调递减的问题。不是计算所有的梯度平方，Adadelta将计算计算历史梯度的窗口大小限制为一个固定值w。

在Adadelta中，无需存储先前的w个平方梯度，而是将梯度的平方递归地表示成所有历史梯度平方的均值。在t时刻的均值E[g2]t只取决于先前的均值和当前的梯度（分量γ类似于动量项）：

E[g2]t=γE[g2]t−1+(1−γ)g2t

我们将γ设置成与动量项相似的值，即0.9左右。为了简单起见，我们利用参数更新向量Δθt重新表示SGD的更新过程：

Δθt=−η⋅gt,i

θt+1=θt+Δθt

我们先前得到的Adagrad参数更新向量变为：

Δθt=−ηGt+ϵ−−−−−√⊙gt

现在，我们简单将对角矩阵Gt替换成历史梯度的均值E[g2]t：

Δθt=−ηE[g2]t+ϵ−−−−−−−−√gt

由于分母仅仅是梯度的均方根（root mean squared，RMS）误差，我们可以简写为：

Δθt=−ηRMS[g]tgt

作者指出上述更新公式中的每个部分（与SGD，动量法或者Adagrad）并不一致，即更新规则中必须与参数具有相同的假设单位。为了实现这个要求，作者首次定义了另一个指数衰减均值，这次不是梯度平方，而是参数的平方的更新：

E[Δθ2]t=γE[Δθ2]t−1+(1−γ)Δθ2t

因此，参数更新的均方根误差为：

RMS[Δθ]t=E[Δθ2]t+ϵ−−−−−−−−−√

由于RMS[Δθ]t是未知的，我们利用参数的均方根误差来近似更新。利用RMS[Δθ]t−1替换先前的更新规则中的学习率η，最终得到Adadelta的更新规则：

Δθt=−RMS[Δθ]t−1RMS[g]tgt

θt+1=θt+Δθt

使用Adadelta算法，我们甚至都无需设置默认的学习率，因为更新规则中已经移除了学习率。

4.5 RMSprop

RMSprop是一个未被发表的自适应学习率的算法，该算法由Geoff Hinton在其Coursera课堂的课程6e中提出。

RMSprop和Adadelta在相同的时间里被独立的提出，都起源于对Adagrad的极速递减的学习率问题的求解。实际上，RMSprop是先前我们得到的Adadelta的第一个更新向量的特例：

E[g2]t=0.9E[g2]t−1+0.1g2t

θt+1=θt−ηE[g2]t+ϵ−−−−−−−−√gt

同样，RMSprop将学习率分解成一个平方梯度的指数衰减的平均。Hinton建议将γ设置为0.9，对于学习率η，一个好的固定值为0.001。

4.6 Adam

自适应矩估计（Adaptive Moment Estimation，Adam）[9]是另一种自适应学习率的算法，Adam对每一个参数都计算自适应的学习率。除了像Adadelta和RMSprop一样存储一个指数衰减的历史平方梯度的平均vt，Adam同时还保存一个历史梯度的指数衰减均值mt，类似于动量：

mt=β1mt−1+(1−β1)gt

vt=β2vt−1+(1−β2)g2t

mt和vt分别是对梯度的一阶矩（均值）和二阶矩（非确定的方差）的估计，正如该算法的名称。当mt和vt初始化为0向量时，Adam的作者发现它们都偏向于0，尤其是在初始化的步骤和当衰减率很小的时候（例如β1和β2趋向于1）。

通过计算偏差校正的一阶矩和二阶矩估计来抵消偏差：

m^t=mt1−βt1

v^t=vt1−βt2

正如我们在Adadelta和RMSprop中看到的那样，他们利用上述的公式更新参数，由此生成了Adam的更新规则：

θt+1=θt−ηv^t−−√+ϵm^t

作者建议β1取默认值为0.9，β2为0.999，ϵ为10−8。他们从经验上表明Adam在实际中表现很好，同时，与其他的自适应学习算法相比，其更有优势。

4.7 算法可视化

下面两张图给出了上述优化算法的优化行为的直观理解。（还可以看看这里关于Karpathy对相同的图片的描述以及另一个简明关于算法讨论的概述）。

在图4a中，我们看到不同算法在损失曲面的等高线上走的不同路线。所有的算法都是从同一个点出发并选择不同路径到达最优点。注意：Adagrad，Adadelta和RMSprop能够立即转移到正确的移动方向上并以类似的速度收敛，而动量法和NAG会导致偏离，想像一下球从山上滚下的画面。然而，NAG能够在偏离之后快速修正其路线，因为NAG通过对最优点的预见增强其响应能力。

图4b中展示了不同算法在鞍点出的行为，鞍点即为一个点在一个维度上的斜率为正，而在其他维度上的斜率为负，正如我们前面提及的，鞍点对SGD的训练造成很大困难。这里注意，SGD，动量法和NAG在鞍点处很难打破对称性，尽管后面两个算法最终设法逃离了鞍点。而Adagrad，RMSprop和Adadelta能够快速想着梯度为负的方向移动，其中Adadelta走在最前面。

(a)损失去面的等高线上SGD优化(b)在鞍点处的SGD优化

图4：来源和全部动画：Alec Radford 

正如我们所看到的，自适应学习速率的方法，即 Adagrad、 Adadelta、 RMSprop 和Adam，最适合这些场景下最合适，并在这些场景下得到最好的收敛性。

4.8 选择使用哪种优化算法？

那么，我们应该选择使用哪种优化算法呢？如果输入数据是稀疏的，选择任一自适应学习率算法可能会得到最好的结果。选用这类算法的另一个好处是无需调整学习率，选用默认值就可能达到最好的结果。

总的来说，RMSprop是Adagrad的扩展形式，用于处理在Adagrad中急速递减的学习率。RMSprop与Adadelta相同，所不同的是Adadelta在更新规则中使用参数的均方根进行更新。最后，Adam是将偏差校正和动量加入到RMSprop中。在这样的情况下，RMSprop、Adadelta和Adam是很相似的算法并且在相似的环境中性能都不错。Kingma等人[9]指出在优化后期由于梯度变得越来越稀疏，偏差校正能够帮助Adam微弱地胜过RMSprop。综合看来，Adam可能是最佳的选择。

有趣的是，最近许多论文中采用不带动量的SGD和一种简单的学习率的退火策略。已表明，通常SGD能够找到最小值点，但是比其他优化的SGD花费更多的时间，与其他算法相比，SGD更加依赖鲁棒的初始化和退火策略，同时，SGD可能会陷入鞍点，而不是局部极小值点。因此，如果你关心的是快速收敛和训练一个深层的或者复杂的神经网络，你应该选择一个自适应学习率的方法。

5 并行和分布式SGD

当存在大量的大规模数据和廉价的集群时，利用分布式SGD来加速是一个显然的选择。SGD本身有固有的顺序：一步一步，我们进一步进展到最小。SGD提供了良好的收敛性，但SGD的运行缓慢，特别是对于大型数据集。相反，SGD异步运行速度更快，但客户端之间非最理想的通信会导致差的收敛。此外，我们也可以在一台机器上并行SGD，这样就无需大的计算集群。以下是已经提出的优化的并行和分布式的SGD的算法和框架。

5.1 Hogwild!

Niu等人[14]提出称为Hogwild!的更新机制，Hogwild!允许在多个CPU上并行执行SGD更新。在无需对参数加锁的情况下，处理器可以访问共享的内存。这种方法只适用于稀疏的输入数据，因为每一次更新只会修改一部分参数。在这种情况下，该更新策略几乎可以达到一个最优的收敛速率，因为CPU之间不可能重写有用的信息。

5.2 Downpour SGD

Downpour SGD是SGD的一种异步的变形形式，在Google，Dean等人[6]在他们的DistBelief框架（TensorFlow的前身）中使用了该方法。Downpour SGD在训练集的子集上并行运行多个模型的副本。这些模型将各自的更新发送给一个参数服务器，参数服务器跨越了多台机器。每一台机器负责存储和更新模型的一部分参数。然而，因为副本之间是彼此不互相通信的，即通过共享权重或者更新，因此可能会导致参数发散而不利于收敛。

5.3 延迟容忍SGD

通过容忍延迟算法的开发，McMahan和Streeter[11]将AdaGraad扩展成并行的模式，该方法不仅适应于历史梯度，同时适应于更新延迟。该方法已经在实践中被证实是有效的。

5.4 TensorFlow

TensorFlow[1]是Google近期开源的框架，该框架用于实现和部署大规模机器学习模型。TensorFlow是基于DistBelief开发，同时TensorFlow已经在内部用来在大量移动设备和大规模分布式系统的执行计算。在2016年4月发布的分布式版本依赖于图计算，图计算即是对每一个设备将图划分成多个子图，同时，通过发送、接收节点对完成节点之间的通信。

5.5 弹性平均SGD

Zhang等人[22]提出的弹性平均SGD（Elastic Averaging SGD，EASGD）连接了异步SGD的参数客户端和一个弹性力，即参数服务器存储的一个中心变量。EASGD使得局部变量能够从中心变量震荡得更远，这在理论上使得在参数空间中能够得到更多的探索。经验表明这种增强的探索能力通过发现新的局部最优点，能够提高整体的性能。

6 优化SGD的其他策略

最后，我们介绍可以与前面提及到的任一算法配合使用的其他的一些策略，以进一步提高SGD的性能。对于其他的一些常用技巧的概述可以参见[10]。

6.1 数据集的洗牌和课程学习

总的来说，我们希望避免向我们的模型中以一定意义的顺序提供训练数据，因为这样会使得优化算法产生偏差。因此，在每一轮迭代后对训练数据洗牌是一个不错的主意。

另一方面，在很多情况下，我们是逐步解决问题的，而将训练集按照某个有意义的顺序排列会提高模型的性能和SGD的收敛性，如何将训练集建立一个有意义的排列被称为课程学习[3]。

Zaremba and Sutskever[20]只能使用课程学习训练LSTM来评估简单程序，并表明组合或混合策略比单一的策略更好，通过增加难度来排列示例。

6.2 批量归一化

为了便于学习，我们通常用0均值和单位方差初始化我们的参数的初始值来归一化。 随着不断训练，参数得到不同的程度的更新，我们失去了这种归一化，随着网络变得越来越深，这种现象会降低训练速度，且放大参数变化。

批量归一化[8]在每次小批量数据反向传播之后重新对参数进行0均值单位方差标准化。通过将模型架构的一部分归一化，我们能够使用更高的学习率，更少关注初始化参数。批量归一化还充当正则化的作用，减少（有时甚至消除）Dropout的必要性。

6.3 Early stopping

如Geoff Hinton所说：“Early Stopping是美丽好免费午餐”（NIPS 2015 Tutorial slides）。你因此必须在训练的过程中时常在验证集上监测误差，在验证集上如果损失函数不再显著地降低，那么应该提前结束训练。

6.4 梯度噪音

Neelakantan等人[12]在每个梯度更新中增加满足高斯分布N(0,σ2t)的噪音：

gt,i=gt,i+N(0,σ2t)

高斯分布的方差需要根据如下的策略退火：

σ2t=η(1+t)γ

他们指出增加了噪音，使得网络对不好的初始化更加鲁棒，同时对深层的和复杂的网络的训练特别有益。他们猜测增加的噪音使得模型更优机会逃离当前的局部最优点，以发现新的局部最优点，这在更深层的模型中更加常见。

总结

在这篇博客文章中，我们初步研究了梯度下降的三个变形形式，其中，小批量梯度下降是最受欢迎的。 然后我们研究了最常用于优化SGD的算法：动量法，Nesterov加速梯度，Adagrad，Adadelta，RMSprop，Adam以及不同的优化异步SGD的算法。 最后，我们已经考虑其他一些改善SGD的策略，如洗牌和课程学习，批量归一化和early stopping。

参考Blog地址出处：

http://blog.csdn.net/woxincd/article/details/7040944

http://www.cnblogs.com/JXPITer/p/6687721.html    

http://blog.csdn.net/google19890102/article/details/69942970