知识点扫盲

啥也不会，慢慢看吧

欧拉函数

在数论，对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）。此函数以其首名研究者欧拉命名(Euler'so totient function)，它又称为Euler's totient function、φ函数、欧拉商数等。 例如φ(8)=4，因为1,3,5,7均和8互质。 从欧拉函数引伸出来在环论方面的事实和拉格朗日定理构成了欧拉定理的证明。

欧拉函数的定义:

    在数论中，对于正整数N,少于或等于N ([1,N]),且与N互质的正整数(包括1)的个数，记作φ(n)。

     φ函数的值：

    φ(x)=x(1-1/p(1))(1-1/p(2))(1-1/p(3))(1-1/p(4))…..(1-1/p(n)) 其中p(1),p(2)…p(n)为x

的所有质因数;x是正整数; φ(1)=1(唯一和1互质的数，且小于等于1)。注意：每种质因数只有一个。

     例如:

         φ(10)=10×(1-1/2)×(1-1/5)=4;

         1 3 7 9

         φ(30)=30×(1-1/2)×(1-1/3)×(1-1/5)=8;

         φ(49)=49×(1-1/7)=42;

 

欧拉函数的性质：

(1)   p^k型欧拉函数:

若N是质数p(即N=p), φ(n)= φ(p)=p-p^(k-1)=p-1。

若N是质数p的k次幂(即N=p^k)，φ(n)=p^k-p^(k-1)=(p-1)p^(k-1)。

(2)mn型欧拉函数

设n为正整数，以φ(n)表示不超过n且与n互素的正整数的个数，称为n的欧拉函数值。若m,n互质，φ(mn)=(m-1)(n-1)=φ(m)φ(n)。

(3)特殊性质:

若n为奇数时，φ(2n)=φ(n)。

对于任何两个互质 的正整数a,n(n>2)有:a^φ(n)=1 mod n (恒等于)此公式即 欧拉定理

当n=p 且 a与素数p互质(即:gcd(a,p)=1)则上式有: a^(p-1)=1 mod n (恒等于)此公式即 费马小定理

 

欧拉函数相关的证明：

(1)   p^k型的欧拉函数的证明：

对于给定的一个素数p: φ(p)=p-1 那么容易证明φ(n)=p^k-p^(k-1)

已知少于或等于p^k的正整数的个数为p^k-1,其中和p^k不互质的正整数有{ p×1,p×2,...,p×(p^(k-1)-1)}，共计p^(k-1)-1个

故: φ(n) = p^k-1-(p^(k-1)-1)=p^k-p^(k-1)。

(2)   mn型的欧拉函数的证明:

因为:x=mn m与n互质(即:gcd(m,n)=1);根据中国剩余定理Z(x)和Z(m)×Z(n)之间存在一一映射，所以x的完全余数集(见下面参考)中的元素的个数Z(x)等于Z(m)×Z(n)元素的个数；而Z(m)×Z(n)= φ(m)φ(n)

故有: φ(mn) =φ(m)φ(n) 成立。

(3)任意正整数的欧拉函数的相关证明:

任意一个整数n都可以表示为其质因子的乘积:

 n=(p(1)*k(1)) *(p(2)*k(2)) *(p(3)*k(3))…(p(i)*k(i))*…*(p(I)*k(I)) 其中I为n 的质因子的个数。

根据(1)(2)的结论，很容易得出它的欧拉函数为:

φ(n)=n(1-1/p(1))(1-1/p(2))(1-1/p(3))(1-1/p(4))…..(1-1/p(i)) 其中I为n 的质因子的个数。

对于任意n>2,2|φ(n) 必定存在 p(i)-1是偶数

 

欧拉定理的相关证明:

(1)  令Z(n)={ X(1),X(2),…,X(φ(n)) }  S={ a*X(1) mod n, a*X(2) mod n ,…,a*X(φ(n)) mod n },则 Z(n)=S。

1)因为a与n互质(即:gcd(a,n)=1), X(i)(1≤i≤φ(n))与n互质(即:gcd(X(i),n)=1);所以

a*X(i)与n互质(即:gcd(a*X(i),n)=1),故 a*X(i) mod n ∈ Z(n)。

     2)若i≠j,那么 X(i)≠X(j) ,又有a与n互质(即:gcd(a,n)==1)，则可得出: a*(X(i)) mod n ≠a*X(j) mod n (消去定律)。

(2)   a^(φ(n))*X(1)*X(2)*X(3)*…*X(φ(n)) mod n

=(a*X(1))*(a*X(2))*(a*X(3))*…*(a*X(φ(n))) mod n

=(a*X(1) mod n)*(a*X(2) mod n)*(a*X(3) mod n)*…*(a*X(φ(n)) mod n) mod n

=X(1)*X(2)*X(3)*…*X(φ(n)) mod n。

对比等式左右两端，因为X(i)(1≤i≤φ(n))与n互质(即:gcd(X(i),n)==1) ,

故: a^φ(n)=1 mod n (恒等于)成立。

 

费马小定理的相关证明：

若正整数 a与素数p互质，则有a^(p-1)=1 mod n(恒等于)

由于φ(p)=p-1 且 a^φ(n)=1 mod n ，又有此处的p==n;

故:a^(p-1)=1 mod n成立。

此定理可以用来简化幂的模运算:

例如: 计算 7^222的个位数，实际上是求7^222被10除的余数。

     且7与10互质，φ(10)=1，由欧拉定理知7^4= 1mod 10

     故7^222=(7^4)^55*(7^2)=>(1^55)*(7^2)=>49=>9 mod 10

 

欧拉函数的延伸:

于或等于n的数中，与n互质的数的总和为：φ(x) * x / 2  (n>1)。

 

相关知识参考:

 

完全余数集合：

定义小于 n 且和 n 互质的数构成的集合为 Z(n) ，称呼这个集合为 n 的完全余数集合。 显然 |Z(n)| ＝φ(n) 。

 

同余定理：

     如果 a mod b = c 则有(a+kb) mod b =c(k为非0整数)

     如果 a mod b = c 则有(ka) mod b =kc (k为正整数)

     (a+b) mod c =((a mod c)+(b mod c )) mod c;

     (a*b) mod c=((a mod c)*(b mod c)) mod c

 

 

 

欧拉函数模板

   (1)直接求小于或等于n,且与n互质的个数:

  int Euler(int n)

{

    int ret=n;

    for(int i=2;i<=sqrt(n);i++)

     if(n%i==0)

      {

        ret=ret/i*(i-1);//先进行除法防止溢出(ret=ret*(1-1/p(i)))

        while(n%i==0)

          n/=i;

     }

    if(n>1)

          ret=ret/n*(n-1);

        return ret;

}

 

筛选模板:求[1,n]之间每个数的质因数的个数

#define size 1000001

int euler[size];

void Init()

{

     memset(euler,0,sizeof(euler));

          euler[1]=1;

     for(int i=2;i<size;i++)

       if(!euler[i])

       for(int j=i;j<size;j+=i)

       {

              if(!euler[j])

               euler[j]=j;

               euler[j]=euler[j]/i*(i-1);//先进行除法是为了防止中间数据的溢出

         }

}

代码：

 1 /*#include<stdio.h> 2 #include<math.h> 3 int main(){ 4     int N,ans; 5     while(~scanf("%d",&N)){ 6             ans=N; 7         for(int i=2;i<=sqrt(N);i++) 8             if(N%i==0){ 9                 ans=ans/i*(i-1);10                 while(N%i==0)N/=i;11             }12             if(N>1)ans=ans/N*(N-1);13        printf("%d\n",ans);14     }15     return 0;16 }17 */18 #include<stdio.h>19 #include<string.h>20 const int MAXN=1000010;21 int dp[MAXN];22 int main(){23     memset(dp,0,sizeof(dp));24     dp[1]=1;25     for(int i=2;i<MAXN;i++){26         if(dp[i])continue;27         for(int j=i;j<MAXN;j+=i){28                 if(!dp[j])dp[j]=j;29             dp[j]=dp[j]/i*(i-1);30         }31     }32     int N;33     while(~scanf("%d",&N))printf("%d\n",dp[N]);34     return 0;35 }

 

/*线性筛O(n)时间复杂度内筛出maxn内欧拉函数值*/int m[maxn],phi[maxn],p[maxn],pt;//m[i]是i的最小素因数，p是素数，pt是素数个数 int make(){    phi[1]=1;    int N=maxn;    int k;    for(int i=2;i<N;i++)    {        if(!m[i])//i是素数            p[pt++]=m[i]=i,phi[i]=i-1;        for(int j=0;j<pt&&(k=p[j]*i)<N;j++)        {            m[k]=p[j];            if(m[i]==p[j])//为了保证以后的数不被再筛，要break            {                phi[k]=phi[i]*p[j];/*这里的phi[k]与phi[i]后面的∏(p[i]-1)/p[i]都一样（m[i]==p[j]）只差一个p[j]，就可以保证∏(p[i]-1)/p[i]前面也一样了*/                break;                }            else                phi[k]=phi[i]*(p[j]-1);//积性函数性质，f(i*k)=f(i)*f(k)        }    }}

数论阶

 编辑

对于(a,n)=1的整数，满足a^r≡1 (mod n ) 的最小整数r,称为a模n的阶。

定义

编辑

设n>1,a是满足（a,n）=1的整数，则必有一个r(1≤r≤n-1)使得a^r≡1 (mod n )

满足a^r≡1 (mod n ) 的最小整数r,称为a模n的阶。

性质

编辑

(1)设（a,n）=1 ，a模n的阶为r. 若正整数N使得a^N≡1(mod n ), 则 r∣N

(2)设（a,n）=1, 则a模n的阶r整除ψ（n）.特别的，若n是素数p, 则a模p的阶整除p-1.（费马定理）

原根的定义

编辑

设m是正整数，a是整数，若a模m的阶等于φ(m)，则称a为模m的一个原根。（其中φ(m)表示m的欧拉函数）

假设一个数g是P的原根，那么g^i mod P的结果两两不同,且有 1<g<P, 0<i<P,归根到底就是g^(P-1) = 1 (mod P)当且仅当指数为P-1的时候成立.(这里P是素数).

简单来说，g^i mod p ≠ g^j mod p （p为素数）

其中i≠j且i, j介于1至(p-1)之间

则g为p的原根。

求原根目前的做法只能是从2开始枚举，然后暴力判断g^(P-1) = 1 (mod P)是否当且仅当指数为P-1的时候成立

而由于原根一般都不大，所以可以暴力得到.

原根的性质

编辑

1）可以证明，如果正整数(a,m) = 1和正整数 d 满足a^d≡1(mod m)，则 d 整除 φ(m)。因此Ordm(a)整除φ(m)。在例子中，

当a= 3时，我们仅需要验证 3 的 1 、2、3 和 6 次方模 7 的余数即可。

2）记δ = Ordm(a)，则a^1，……a^(δ-1)模 m 两两不同余。因此当a是模m的原根时，a^0,a^1，……a^(δ-1)构成模 m

的简化剩余系。

3）模m有原根的充要条件是m= 1,2,4,p,2p,p^n，其中p是奇质数，n是任意正整数。

4）对正整数(a,m) = 1，如果 a 是模 m 的原根，那么 a 是整数模n乘法群（即加法群 Z/mZ的可逆元，也就是所有

与 m 互素的正整数构成的等价类构成的乘法群）Zn的一个生成元。由于Zn有 φ(m)个元素，而它的生成元的个数就

是它的可逆元个数，即 φ(φ(m))个，因此当模m有原根时，它有φ(φ(m))个原根。

原根的例子

编辑

设m= 7，则φ（7）等于6。

设a= 2，由于2^3=8≡1(mod 7)，2^6=64≡1(mod7)，而2!=3，2^3≡2^6(mod7)，所以 2 不是模 7 的一个原根。设a= 3，由于3^1≡3(mod 7)，3^2≡2(mod 7)，3^3≡6(mod 7)，3^4≡4(mod 7)，3^5≡5(mod 7)，3^6≡1(mod 7)，所以 3 是模 7 的一个原根。

补充一点，根据原根的性质1，只需要验证3^1，3^2，3^3，3^6即可，这样可以简化运算。

转自：点击打开链接

1.原根定义

假设一个数g对于P来说是原根，那么g^i mod P的结果两两不同,且有 1<g<P, 1<i<P,那么g可以称为是P的一个原根

简单来说，g^i mod p ≠ g^j mod p （p为素数）

其中i≠j且i, j介於1至(p-1)之间

则g为p的原根。

 

简单的来说，如果g是P的原根，那么g的（1...P-1）次幂mod P的结果一定互不相同。

 

那么简化一下：

首先看一下欧拉定理：

欧拉定理（也称费马-欧拉定理或欧拉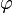函数定理）是一个关于同余的性质。欧拉定理表明，若为正整数，且互素

（即），则

因此，在时，定义对模的指数为使成立的最小的正整数。

由前知 一定小于等于 ，若，则称是模的原根。

 

归根到底，如果g是P的原根，就是g^(P-1) = 1 (mod P)当且仅当指数为P-1的时候成立.(这里P是素数).

 

 

 

例如：

设m= 7，则φ（7）等于6。φ（7）表示7的欧拉函数。

设a= 2，由于2^3=8≡1(mod 7)，而3<6，所以 2 不是模 7 的一个原根。设a= 3，由于3^1≡3(mod 7)，3^2≡2(mod 7)，3^3≡6(mod 7)，

3^4≡4(mod 7)，3^5≡5(mod 7)，3^6≡1(mod 7)，所以 3 是模 7 的一个原根。

 

2.如何求解：

一、枚举

从2开始枚举，然后暴力判断g^(P-1) = 1 (mod P)是否当且当指数为P-1的时候成立

而由于原根一般都不大，所以可以暴力得到.

二、讲究方法

例如求任何一个质数x的任何一个原根，一般就是枚举2到x-1，并检验。有一个方便的方法就是，求出x-1所有不同的质因子p1,p2...pm，

对于任何2<=a<=x-1,判定a是否为x的原根，只需要检验a^((x-1)/p1),a^((x-1)/p2),...a^((x-1)/pm)这m个数中，是否存在一个数mod x为1，

若存在，a不是x的原根，否则就是x的原根。

原来的复杂度是O(P-1)，现在变成O(m)*log（P-1）m为x-1质因子的个数。很明显质因子的个数远远小于x-1。

证明可用欧拉定理和裴蜀定理：

裴蜀定理

说明了对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性丢番图方程（称为裴蜀等式）：

ax + by = m 
有解当且仅当m是d的倍数。裴蜀等式有解时必然有无穷多个整数解，每组解x、y都称为裴蜀数，可用辗转相除法求得。

例如，12和42的最大公因子是6，则方程12x + 42y = 6有解。事实上有(-3)×12 + 1×42 = 6及4×12 + (-1)×42 = 6。

特别来说，方程 ax + by = 1 有解当且仅当整数a和b互素。

裴蜀等式也可以用来给最大公约数定义：d其实就是最小的可以写成ax + by形式的正整数。这个定义的本质是整环中“理想”的概念。

因此对于多项式整环也有相应的裴蜀定理。

证明

[html] view plain copy

1. 若存在，那么显然的事情  
2.   
3. 否则，假设存在一个t<phi(x)=x-1使得a^t = 1 (mod x)  
4.   
5. 那么由裴蜀定理，一定存在一组k,r使得kt=(x-1)r+gcd(t,x-1)  
6.   
7. 而由欧拉定理有，a^(x-1) = 1 (mod x)  
8.   
9. 于是1 = a^(kt) = a^(xr-r+gcd(t,x-1)) = a^gcd(t,x-1) (mod x)  
10.   
11. 而t<x-1故gcd(t,x-1)<x-1  
12.   
13. 又gcd(t,x-1)|x-1 于是gcd(t,x-1)必整除(x-1)/p1,(x-1)/p2...(x-1)/pm其中至少一个，设其一为(x-1)/pi  
14.   
15. 那么a^((x-1)/pi) = (a^gcd(t,x-1))^s = 1^s = 1 (mod x)  
16.   
17. 这与假设矛盾  

转自wiki

在数论，特别是整除理论中，原根是一个很重要的概念。

对于两个正整数{\displaystyle (a,m)=1}，由欧拉定理可知，存在正整数{\displaystyle d\leq m-1}， 比如说欧拉函数{\displaystyle d=\varphi (m)}，即小于

等于{\displaystyle m}的正整数中与{\displaystyle m}互素的正整数的个数，使得{\displaystyle a^{d}\equiv 1{\pmod {m}}}。

由此，在{\displaystyle (a,m)=1}时，定义{\displaystyle a}对模{\displaystyle m}的指数{\displaystyle \delta m(a)}为使{\displaystyle a^{d}\equiv 1{\pmod {m}}}成立的最小的正整数{\displaystyle d}。由前知

{\displaystyle \delta m(a)} 一定小于等于 {\displaystyle \varphi (m)}，若{\displaystyle \delta m(a)=\varphi (m)}，则称{\displaystyle a}是模{\displaystyle m}的原根。

设{\displaystyle m=7}，则{\displaystyle \varphi (m)}等于6。

• 设{\displaystyle a=2}，由于{\displaystyle 2^{3}=8\equiv 1{\pmod {7}}}，而{\displaystyle \displaystyle 3<6}，所以 2 不是模 7 的一个原根。
• 设{\displaystyle a=3}，由于{\displaystyle 3^{1}\equiv 3{\pmod {7}}}，{\displaystyle 3^{2}\equiv 2{\pmod {7}}}，{\displaystyle 3^{3}\equiv 6{\pmod {7}}}，{\displaystyle 3^{4}\equiv 4{\pmod {7}}}
• ，{\displaystyle 3^{5}\equiv 5{\pmod {7}}}，{\displaystyle 3^{6}\equiv 1{\pmod {7}}}，因此有{\displaystyle Ord_{7}(3)=6=\varphi (7)}，所以 3 是模 7 的一个原根。

性质[编辑]

• 可以证明，如果正整数{\displaystyle (a,m)=1}和正整数 d 满足{\displaystyle a^{d}\equiv 1{\pmod {m}}}，则 {\displaystyle Ord_{m}(a)} 整除 d。^[1]
• 因此{\displaystyle Ord_{m}(a)}整除{\displaystyle \varphi (m)}。在例子中，当{\displaystyle a=3}时，我们仅需要验证 3 的 2、3 次方模 7 的余数即可，
• 如果其中有一个是1，则3就不是原根。

• 记{\displaystyle \delta =Ord_{m}(a)}，则{\displaystyle a^{0},a^{1},a^{2}\cdots ,a^{\delta -1}}模 m 两两不同余。因此当{\displaystyle a}是模{\displaystyle m}的原根时，{\displaystyle a^{0},a^{1},a^{2}\cdots ,a^{\delta -1}}
• 构成模 m 的简化剩余系。

• 模{\displaystyle m}有原根的充要条件是{\displaystyle m=2,4,p^{n},2p^{n}}，其中{\displaystyle p}是奇素数，{\displaystyle n}是任意正整数。

• 对正整数{\displaystyle (a,m)=1}，如果 a 是模 m 的原根，那么 a 是整数模n乘法群（即加法群 Z/mZ 的可逆元，也就是所有与
• m 互素的正整数构成的等价类构成的乘法群）Z_n^×的一个生成元。由于Z_n^×有 {\displaystyle \varphi (m)}个元素，而它的生成元的个数
• 就是它的可逆元个数，即 {\displaystyle \varphi (\varphi (m))}个，因此当模{\displaystyle m}有原根时，它有{\displaystyle \varphi (\varphi (m))}个原根。

除了直接运算以外，至今还没有一个办法可以找到模特定m时的原根，但假如已知模m有一个原根，则可找出它其他的原根。

最小原根[编辑]

模 p 的最小原根 g _p 定义为在 1 到 p-1 中最小的原根。数学家已经给出最小原根的上界及下界的一些限制。

伯吉斯(1962)证明对任何 ε>0，存在一个 C>0，使得 {\displaystyle g_{p}\leq Cp^{{\frac {1}{4}}+\epsilon }}。

Emil Grosswald (1981) 证明如果 {\displaystyle p>e^{e^{24}}}，则 {\displaystyle g_{p}<p^{0.499}}。

生成元[编辑]

{\displaystyle (\mathbb {Z} /n\mathbb {Z} )^{\times }} 是循环群当且仅当 {\displaystyle \varphi (n)=\lambda (n).} 这在 n 为奇质数的幂次、奇质数幂次 2 倍、2 和 4 成立，此时也称一

个生成元为模 n 的原根。

因为所有 {\displaystyle (\mathbb {Z} /n\mathbb {Z} )^{\times },} n = 1, 2, ..., 7 是循环群，上述结论的另一种说法是：如果 n < 8 那么 {\displaystyle \;(\mathbb {Z} /n\mathbb {Z} )^{\times }} 有原根；

如果 n ≥ 8，且不能被 4 或者两个不同的奇质数整除，{\displaystyle \;(\mathbb {Z} /n\mathbb {Z} )^{\times }} 有原根。

( A033948 = 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19, 22, 23, 25, 26, 27, 29, 31, 34, 37, 38, 41, 43, 46, 47, 49, 50, ... )

一般情形每个直积因子循环有一个生成元。

传递闭包

1、问题引入

　　一个有n个顶点的有向图的传递闭包为：有向图中的初始路径可达情况可以参见其邻接矩阵A，邻接矩阵中A[i,j]表示i到j是否直接可达，

若直接可达，则A[i,j]记为1，否则记为0；两个有向图中i到j有路径表示从i点开始经过其他点（或者不经过其他点）能够到达j点，如果i到j

有路径，则将T[i,j]设置为1，否则设置为0；有向图的传递闭包表示从邻接矩阵A出发，求的所有节点间的路径可达情况，该矩阵就为所要

求的传递闭包矩阵。。。

例如：

有向图为：

由该有向图可以得到初始的邻接矩阵为：

那么warshall传递闭包算法的目的就是由邻接矩阵出发，进行探索求出最终的传递闭包：

通俗点：

所谓传递性，可以这样理解：对于一个节点i，如果j能到i，i能到k，那么j就能到k。求传递闭包，就是把图中所有满足这样传递性的节点

都弄出来，计算完成后，我们也就知道任意两个节点之间是否相连。 

割

编辑

割：设Ci为网络N中一些弧的集合，若从N中删去Ci中的所有弧能使得从源点Vs到汇点Vt的路集为空集时，称Ci为Vs和Vt间的一个割。通俗理解，一个图或网络的割，表示一个切面或切线，将图或网络分为分别包含源点和漏点的两个子集，该切线或切面与网络相交的楞或边的集合，称为图像的割。

最小割

编辑

最小割：图中所有的割中，边权值和最小的割为最小割。

实例

编辑

实例：如右图所示的最小割集为 --表示无序对，->表示有序对

C1：{①->③，①->⑤}

C2：{④->②， ⑤->②}

C3：{③--④，③-- ⑤，①-> ⑤}

C4：{③--④，④-- ⑤， ⑤->②}

C5：{①-> ⑤，③-- ⑤，④-- ⑤，④->②}[1] 

C6：{①->③，③- - ⑤，④-- ⑤， ⑤->②}

  二分图最小点覆盖和最大独立集都可以转化为最大匹配求解。在这个基础上，把每个点赋予一个非负的权值，这两个问题就转化为：二分图最小点权

覆盖和二分图最大点权独立集。

 、

    二分图最小点权覆盖

    从x或者y集合中选取一些点，使这些点覆盖所有的边，并且选出来的点的权值尽可能小。

建模：

    原二分图中的边(u,v)替换为容量为INF的有向边(u,v)，设立源点s和汇点t，将s和x集合中的点相连，容量为该点的权值；将y中的点同t相连，容量为

该点的权值。在新图上求最大流，最大流量即为最小点权覆盖的权值和。

 

二分图最大点权独立集

    在二分图中找到权值和最大的点集，使得它们之间两两没有边。其实它是最小点权覆盖的对偶问题。答案=总权值-最小点覆盖集。具体证明参考

胡波涛的论文。

图上的流动 - flow
定向图的要素，顶点集V={x,y,z…},定向边E={xy,yz,…},其中xy表示由x指向y的一条变，所以xy不一定等于yx. 图上的流是一个函数，

对每一条变指定一个非负实数，即流量，记作f(xy).因而图上的流也可以看作一个函数：f: Eà[0,infty).

对于图上的顶点x来说，将通过x的流分作两类。其一是由x流出，即形如xy的边。另一类是流入，即形如zx的边。
图上给定一个流f, 则可将图上的顶点分作3类。
流出的量等于流入的量。
流出的量大于流入的量，这样的顶点称作源，source. 用记号s来表示。
流出的量小于流入的量，这样的顶点称作汇，sink. 用记号t来表示。
因而，除掉源和汇，其他的顶点没有产生额外的流量，也没有流消失。为简单起见，本文总是假设源和汇各自都只有一个。

实际上，有多个source或者sink的流很容易归结为只有一个的情形。
容易证明，流出source的流量等于流入sink的流量，这个数称为流f的流量。
例子：电路。其中的源就是电源，包括发电机。其中的汇就是消耗电能的设备。当然，这里假定电路本身没有电力的损耗。
通常，线路上的流有容量限制。确切的说，定向图上的每一条定向边xy, 都对应到一个非负实数C(xy)，即容量，capacity.
在一个定向图中，给定每条边的容量，我们能否找到满足某些条件的流f, 使得对每一条边xy, 都有f(xy)=<C(xy).
比如，在所有的满足限制条件f(xy)=<C(xy)的流中，是否存在一个具有最大流量的流。当然这是一个初等而简单的问题。

其证明类似于数学分析中所有与紧性有关的定理。首先，满足上述限制条件的流，其流量有一个绝对的一致上界，

因而存在一个最小上界。因而就可以找到流的一个序列f_n, 使得f_n的流量趋向于这个最小上界。序列f_n一定有一个子序列收敛到某个流，

这个流就具有最大流量。
所以，具有容量限制的定向图上，一定存在最大流。
最大流最小割定理。max-flow min-cut theorem.
定向图(V,E), V为顶点集，E为定向边的集合。对V的不相交的子集X,Y, 令E(X,Y)={定向边xy| 其中x在X中，y在Y中}.

对取值为实数的函数g: EàR(实数)，令g(X,Y)=sum g(x,y), 亦即所有由X指向Y的定向边对应的函数值之和。
设S为V的子集，若source在S中，同时sink不在S中，则称S为一个割，cut. 也可以简单的说，割就是可以分离source和sink的顶点集。
设定向图上有容量函数C, 对于一个割S, 定义S的容量为C(S,V-S)= sum C(xy), 其中x在S中，y不在S中。
设(V,E,C)为有容量限制的定向图，f为其上的一个流，满足容量限制。
简单事实：f的流量 =< 任意一个割的容量。
最大流最小割定理(Ford-Fulkerson, 1962): 存在一个割，其容量 = 最大流的流量。
亦即，具有容量限制的最大流的流量 = 最小割的容量。
证明纲要。
由于具有最大流量的流存在，所以我们可以取一个最大流f.
递归的定义一个顶点集S如下，
首先，source在 S中。
其次，若x在S中，且f(xy)<C(xy), 则y也在S中。
最后，若x在S中，且f(yx)>0, 则y也在S中。
反复使用上述过程，最后可以得到一个由顶点构成的集合，即S. 由于图中只有有限多个顶点，所以上述过程也一定会在有限多个步骤之后终止。

还需证明sink不在S中。如下。
假如sink在S中，则有一列顶点，x_1=source, x_2, …, x_n=sink.使得
r_i = max{c(x_ix_{i+1})-f(x_ix_{i+1}), f(x_{i+1}x_i)}>0
这个式子不大容易看清，我们重新叙述如下，对于该序列中的任意两个相邻顶点x,y,其中x=x_i在y=x_{i+1}前面，都有 C(xy)-f(xy)>0

或者 f(yx)>0, 取二者当中较大的一个，这个数就是r_i. 然后取所有r_i中最小的一个，有限多个正数的最小值还是一个正数(严格大于0)。

记这个正数为r. 由此对f作一些修改可以构造一个新的流，若边xy在上述序列中，则将流量f(xy)修改为f(xy)+r. 否则就不作改变。

这样得到的函数确实是一个流，满足容量限制，而且其流量比f的流量要大r>0. 这就和f是最大流矛盾。这就证明了S确实为一个割。
下面说明割S的容量 = 流f的流量。首先有等式，
f的流量 = f(S,V-S) – f(V-S,S).
由S的构造，容易看出第一项 f(S,V-S) = C(S,V-S) = 割S的容量。第二项f(V-S,S) = 0. 证毕。
记号V-S表示不在S中的顶点全体，亦即表示集合S在V中的余集。
最大流最小割的整性定理：若容量C(xy)都是整数，则最大流f的流量f(xy)也都是整数。
实际上，当每条边的容量都是整数时，max-flow min-cut定理的证明也给出了一个很好的算法。如下，构造流的序列f_0, f_1, f_2, …

使得对每一条边，其流量都是递增的。
流f_0, 对每条边赋予流量f_0(xy)=0. 这是一个平凡的流。对于流f_i, 如max-flow min-cut定理的证明，构造相应的集合S. 则有两种情形。

若sink在S中，如此，我们将终止这个构造过程。另一种情形是sink不在S中，这样可找到一条由source到sink的链，

亦即一些首尾依次相连的边，这些边连接着source和sink, 将这条边的每一个的流量增加1, 这样得到一个新的流f_{i+1}.

这个程序将在有限多个步骤之后终止，最后所得即为一个在每条边上的流量都是整数的流。
最大流最小割的对偶定理
前面，我们对于流量进行的限制是要求每一条边的流量有一个上限，即容量C(xy). 我们也可以对每一个顶点的容量进行限制，

即要求流入每一个顶点的流量有一个上限。注意到对每一个顶点，我们对于流入和流出进行了区分的，在一个不是 source或sink的顶点，

流入的流量等于流出的流量。因而二者都是有限的。对于这样的图，我们可以类似的定义割、割得容量这两个概念。

此时的割称为 Vertex-cut, 定义为V-{source,sink}的一个子集S使得，在V-S不可能存在一个具有正流量的流。
通常我们不限制source和sink的流量，或者说，这两个顶点的容量是无穷大。
对顶点限制流量的定向图，可以用一个小的技巧转化为我们已经证明过的对边的容量进行限制的定向图。于是我们有下述的定理。
定理：设定向图(V,E)的顶点有容量限制，但在source和sink处没有容量限制，则关于顶点的最小割的容量 = 最大流的流量。
Source 和sink多于1个的情形。
设s_1, s_2, … ,s_n为全部的source, 我们将之转化为只有一个sourece的情形。在原来的定向图中添加一个顶点s, 以及定向边ss_i,

在这些边上的容量限制取作无穷大。由此即可转换为只有一个source的情形。
对于sink完全类似的处理即可。
注意到，max-flow min-cut定理中，如果某些边的容量为无穷大，定理的结论仍然成立，只不过此时的最大流的流量可能是无穷大。

证明的方法也没有多大变化，无非就是稍稍改变一下其中的某些叙述。

图的连通性 - connectivity
基本定理(Menger, 1927)
(1)[vertex form] 设s, t为图G中两个不相邻的顶点，则分离s, t的最少顶点数 = 连接s, t的独立道路的最大数目。
(2)[edge form] 设s, t为图G中两个不同的顶点，则分离s, t的最少边数 = 连接s, t的不相交道路的最大数目。
定理中术语的解释。
s, t为不相邻的顶点是指没有直接连接s, t的边。
所谓分离s, t的顶点集合S, 是指s, t都不在S中，且在原图中去掉S中的顶点，则s, t在剩下的图中不能相互连接。亦即，

任意连接s, t的道路至少通过S中的一个顶点。
连接s, t的道路是指，一些首尾相接的边sa, ab, bc, …, xy, yt, 并且所有的顶点互不相同。例如sa, ab, bc, cd, da, at不是一条道路。
两条连接s, t的道路称为独立的，若这两条道路的公共点只有s, t.
不相交的道路，是指这些道路没有相同的边，但是可以有共同的顶点。
证明。
(1) 由图G构造一个相应的定向图，将图G中的每一条边xy都换作两条定向边xy及yx, 在 除开s,t 以外的每个顶点上赋予容量1.

由此限定的流在每条边上的流量只能为０或者１. 将顶点s, t看作source和sink. 于是由整性最大流最小割定理，

可知存在一个具有最大流量的整数流。容易看出：连接s, t的独立道路的最大数目 = 最大流量 = 分离s, t需要的最少顶点数。
(2) 类似(1). 只需将其中对于顶点的容量限制改换为对于边的容量限制即可。
证毕。
若图中任意两个顶点都可以用一些边连接起来，则称这个图为连通的。
G为连通图，则G称为k-连通的，k-connected, 若
当Gz中顶点个数为(k+1)时，G为完全图，亦即任意两个顶点之间都有边相连接。
当G中的顶点个数至少为(k+2)时，去掉其中的任意(k-1)个顶点，所得到的图仍然连通。
注意，连通图可以看作1-连通的。
一个图称为k-edge-connected, 若去掉其中的任意(k-1)条边，剩下部分仍然连通。
使得图G为k-连通的最大数字k称为图G的连通度，connectivity.
使得图G为k-edge-connected的最大数字k称为图G的edge-connectivity.
约定，不连通的图，其两种连通度都规定为0.
Menger定理的推论：
(1) 图G是k-connected的 iff 对于图G中任意两个顶点，至少有k条独立的道路连接这两个顶点。
(2) 图G是k-edge-connected的 iff 对于图G中任意两个顶点，至少有k条不相交的道路连接这两个顶点。
Menger定理是在1927年证明的，而max-flow min-cut定理则是在1962年证明的。我们是由max-flow min-cut定理证明Menger定理。反过来，

也可以用Menger定理证明max-flow min-cut定理。因而人们通常这样叙述：Menger定理与max-flow min-cut定理是等价的。

两个数学定理等价，

这个说法多少有点古怪：两个都正确的命题之间是等价的。这两个定理也都可以单独证明。
iff = if and only if, 这个简洁的用语充分的反映出来英语的某些优势。
另外Menger定理的结论“分离s, t的最少顶点数 = 连接s, t的独立道路的最大数目”用英文可以叙述为：

The minimal number of vertices separate s from t = the maximal number of independent s-t paths.

似乎英文要简明一些。当然二者包含的信息还是相同的，用哪种语言并不能从本质上简化定理。

哈密顿图的判定是世界级难题。

设G是n阶无向简单图，若对于G中任意不相邻的顶点u、v，均有d(u)+d(v)>=n-1，则说明G中存在哈密顿通路。

不过，这个条件只是充分条件，而不是必要条件。

也就是说，满足该条件一定存在哈密顿通路，但不满足该条件不一定不存在哈密顿通路。

如下图便不满足，但它存在哈密顿路。

所以要判断哈密顿回路和哈密顿路径一般通过深搜回溯去判定，代码：

[cpp] view plain copy

1. #include <algorithm>  
2. #include <iostream>  
3. #include <string.h>  
4. #include <vector>  
5. using namespace std;  
6. const int maxn = 1005;  
7. vector<int> G[maxn];  
8. int n, m, root;  
9. int vis[maxn];  
10. int HamiPath(int cur, int cnt)  
11. {  
12.     if(cnt == n)  
13.     {  
14.         //判定哈密顿回路   
15.         for(int i = 0; i < G[cur].size(); ++i)  
16.         if(G[cur][i] == root) return 1;  
17.         return 0;  
18.         //return 1; //判定哈密顿路直接return 1即可   
19.     }  
20.     for(int i = 0; i < G[cur].size(); ++i)  
21.     {  
22.         int v = G[cur][i];  
23.         if(vis[v]) continue;  
24.         vis[v] = 1;  
25.         if(HamiPath(v, cnt+1)) return 1;  
26.         vis[v] = 0;  
27.     }  
28.     return 0;  
29. }  
30. int main()  
31. {  
32.     cin >> n >> m;  
33.     memset(vis, 0, sizeof vis);   
34.     for(int i = 1; i <= n; ++i) G[i].clear();  
35.     for(int i = 1; i <= m; ++i)  
36.     {  
37.         int u, v;  
38.         scanf("%d %d", &u, &v);  
39.         G[u].push_back(v);  
40.         G[v].push_back(u);  
41.     }  
42.     root = 1;  
43.     if(HamiPath(root, 1)) puts("exist");  
44.     else puts("not exist");  
45.     return 0;  
46. }  

更为重要的是欧拉图的判定：

定义：

欧拉回路：每条边恰好只走一次，并能回到出发点的路径
欧拉路径：经过每一条边一次，但是不要求回到起始点

欧拉回路存在性的判定：

一、无向图
每个顶点的度数都是偶数，则存在欧拉回路。

二、有向图（所有边都是单向的）
每个节顶点的入度都等于出度，则存在欧拉回路。

欧拉路径存在性的判定：

一、无向图
一个无向图存在欧拉路径，当且仅当该图所有顶点的度数为偶数或者除了两个度数为奇数外其余的全是偶数。

二、有向图

一个有向图存在欧拉路径，当且仅当该图所有顶点的度数为零或者一个顶点的度数为1，另一个度数为-1，其他顶点的度数为0。(有向图的度数等于该点的出度+入度，其中出度和入度一正一负)

然后较难的是混合图的欧拉回路和欧拉路径是否存在的判定：

混合图的欧拉回路的判定就是上一篇博客的例题通过最大流求解，也有自己的个人理解。

混合图的欧拉路径的判定，这个人的方法可以实现：求欧拉路径的第一步一定是求欧拉回路，在混合图上也不例外，如何判断混合图欧拉回路问题的存在性呢？首先，用上篇博客的方法判断该图是否存在欧拉回路，如果存在，欧拉路径一定存在。如果欧拉回路不存在，那么我们枚举欧拉路径的起点和终点，连接一条无向边，然后再用最大流判断是否存在欧拉回路即可。